• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Text 4. Cosmology and the Big Bang

Internet Assignment:

Get information from the Internet to confirm or refuse the following statement:

Now, it follows from the equations of Einstein's general relativity that this positively closed universe cannot continue to expand forever. After it reaches a stage of maximum expansion, it collapses back in on itself, finally to reach zero size again in a kind of big bang in reverse.

As far as we can tell from using our most powerful telescopes – both optical and radio – the universe, on a very large scale, appears to be rather uniform; but, more remarkably, it is expanding. The farther away that we look, the more rapidly the distant galaxies (and even more distant quasars) appear to be receding from us. It is as though the universe itself was created in one gigantic explosion – an event referred to as the big bang, which occurred some ten thousand million years ago.[15] Impressive further support for this uniformity, and for the actual existence of the big bang, comes from what is known as the black-body background radiation. This is thermal radiation – photons moving around randomly, without discernible source – corresponding to a temperature of about 2.7° absolute (2.7 K), i.e. -270.3° Celsius, or 454.5° below zero Farenheit. This may seem like a very cold temperature – as indeed it is! – but it appears to be the leftover of the flash of the big bang itself! Because the universe has expanded by such a huge factor since the time of the big bang, this initial fireball has dispersed by an absolutely enormous factor. The temperatures in the big bang far exceeded any temperatures that can occur at the present time, but owing to this expansion, that temperature has cooled to the tiny value that the black-body background has now. The presence of this background was predicted by the Russian-American physicist and astronomer George Gamow in 1948 on the basis of the now-standard big-bang picture. It was first observed (accidentally) by Penzias and Wilson in 1965.

I should address a question that often puzzles people. If the distant galaxies in the universe are all receding from us, does that not mean that we ourselves are occupying some very special central location? No it does not! The same recession of distant galaxies would be seen wherever we might be located in the universe. The expansion is uniform on a large scale, and no particular location is preferred over any other. This is often pictured in terms of a balloon being blown up (Fig. 1). Suppose that there are spots on the balloon to represent the different galaxies, and take the two-dimensional surface of the balloon itself to represent the entire three-dimensional spatial universe. It is clear that from each point on the balloon, all the other points are receding from it. No point on the balloon is to be preferred, in this respect, over any other point. Likewise, as seen from the vantage point of each galaxy in the universe, all other galaxies appear to be receding from it, equally in all directions.

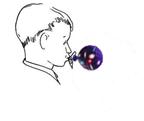
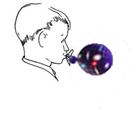
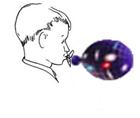
Fig. 1. The expansion of the universe can be likened to the surface of a balloon being blown up. The galaxies all recede from one another

This expanding balloon provides quite a good picture of one of the three standard so-called Friedmann-Robertson-Walker (FRW) models of the uni­verse – namely the spatially closed positively curved FRW-model. In the other two FRW-models (zero or negative curvature), the universe expands in the same sort of way, but instead of having a spatially finite universe, as the surface of the balloon indicates, we have an infinite universe with an infinite number of galaxies.

In the easier to comprehend of these two infinite models, the spatial geometry is Euclidean, i.e. it has zero curvature. Think of an ordinary flat plane as representing the entire spatial universe, where there are points marked on the plane to represent galaxies. As the universe evolves with time, these galaxies recede from one another in a uniform way. Let us think of this in space-time terms. Accordingly, we have a different Euclidean plane for each 'moment of time', and all these planes are imagined as being stacked one above the other, so that we have a picture of the entire space-time all at once (Fig. 2). The galaxies are now represented as curves – the world-lines of the galaxies' histories – and these curves move away from each other into the future direction. Again no particular galaxy world-line is preferred.

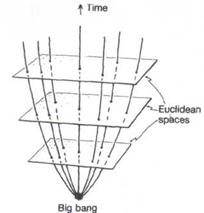
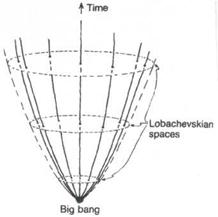
Fig. 2. Space-time picture of an ex­panding universe with Euclidean spatial sections (two space dimensions de­picted)	Fig. 3. Space-time picture of an ex­panding universe with Lobachevskian spatial sections (two space dimensions depicted)

For the one remaining FRW-model, the «negative-curvature model, the spatial geometry is the non-Euclidean Lobachevskian. For the space-time description, we need one of these Lobachevsky spaces for each 'instant of time', and we stack these all on top of one another to give a picture of the entire space-time (Fig. 3). Again the galaxy world-lines are curves moving away from each other in the future direction, and no galaxy is preferred.

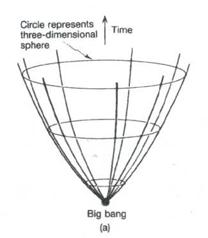
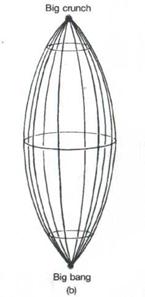
Of course, in all these descriptions we have suppressed one of the three spatial dimensions to give a more visualizable three-dimensional space-time than would be necessary for the complete four-dimensional space-time picture. Even so, it is hard to visualize the positive-curvature space-time without discarding yet another spatial dimension! Let us do so, and represent the positively curved closed spatial universe by a circle (one-dimensional), rather than the sphere (two-dimensional) which had been the balloon's surface. As the universe expands, this circle grows in size, and we can represent the space-time by stacking these circles (one circle for each 'moment of time') above one another to obtain a kind of curved cone (Fig. 4). Now, it follows from the equations of Einstein's general relativity that this positively closed universe cannot continue to expand forever. After it reaches a stage of maximum expansion, it collapses back in on itself, finally to reach zero size again in a kind of big bang in reverse (Fig. 4). This time-reversed big bang is sometimes referred to as the big crunch. The negatively curved and zero-curved (infinite) universe FRW-models do not recollapse in this way. Instead of reaching a big crunch, they continue to expand forever.

At least this is true for standard general relativity in which the so-called cosmological constant is taken to be zero. With suitable non-zero values of this cosmological constant, it is possible to have spatially infinite universe models which recollapse to a big crunch, or finite positively curved models which expand indefinitely. The presence of a non-zero cosmological constant would complicate the discussion slightly, but not in any significant way for our purposes. For simplicity, I shall take the cosmological constant to be zero.[16] At the time of writing, the cosmological constant is known observationally to be very small, and the data are consistent with its being zero. (For further information on cosmological models, see Rindler 1977.)

Fig. 4. (a) Space-time picture of an expanding universe with spherical spatial sections (only one space dimension depicted), (b) Eventually this universe re-collapses to a final big crunch

Unfortunately the data are not yet good enough to point clearly to one or other of the proposed cosmological models (nor to determine whether or not the presence of a tiny cosmological constant might have a significant overall effect). On the face of it, it would appear that the data indicate that the universe is spatially negatively curved (with Lobachevsky geometry on the large scale) and that it will continue to expand indefinitely. This is largely based on observations of the amount of actual matter that seems to be present in visible form. However, there may be huge amounts of invisible matter spread throughout space, in which case the universe could be positively curved, and it could finally recollapse to a big crunch – though only on a time-scale far larger than the 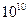years, or so, for which the universe has been in existence. For this recollapse to be possible there would have to be some thirty times as much matter permeating space in this invisible form – the postulated so-called 'dark matter' – than can be directly discerned through telescopes. There is some good indirect evidence that a substantial amount of dark matter is indeed present, but whether there is enough of it 'to close the universe' (or make it spatially flat) – and recollapse it – is very much an open question.

Переглядів: 519