• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

What is the very essence of mathematical visualization? Key-words: magnification, abstract mathematics, complex numbers, miracles of mathematics.

We are now in a position to see how the Mandelbrot set is defined. Let 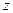be some arbitrarily chosen complex number. Whatever this complex number is, it will be represented as some point on the Argand plane. Now consider the mapping whereby 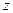is replaced by a new complex number, given by

,

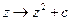where с is another fixed (i.e. given) complex number. The number 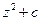will be represented by some new point in the Argand plane. For example, if 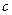happened to be given as the number 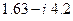, then 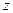would be mapped according to

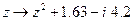
so that, in particular, 3 would be replaced by

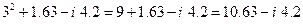
and 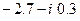would be replaced by

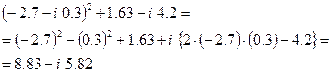
When such numbers get complicated, the calculations are best carried out by an electronic computer.

Now, whatever с may be, the particular number 0 is replaced, under this scheme, by the actual given number 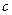. What about 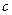itself? This must be replaced by the number 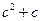Suppose we continue this process and apply the replacement to the number 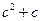; then we obtain

.

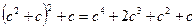Let us iterate the replacement again, applying it next to the above number to obtain

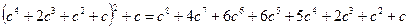
and then again to this number, and so on. We obtain a sequence of complex numbers, starting with 0:

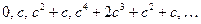
Now if we do this with certain choices of the given complex number c, the sequence of numbers that we get in this way never wanders very far from the origin in the Argand plane; more precisely, the sequence remains bounded for such choices of с which is to say that every member of the sequence lies within some fixed circle centred at the origin (see Fig. 1). A good example where this occurs is the case 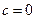, since

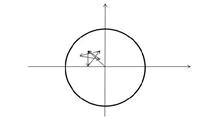
Fig. 1. A sequence of points in the Argand plane is bounded if there is some fixed circle that contains all the points. (This particular iteration starts with zero and has ).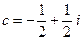

in this case, every member of the sequence is in fact 0. Another example of bounded behaviour occurs with 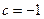, for then the sequence is: 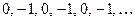; and yet another example occurs with 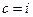, the sequence being 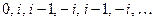. However, for various other complex numbers с the sequence wanders farther and farther from the origin to indefinite distance; i.e. the sequence is unbounded, and cannot be contained within any fixed circle. An example of this latter behaviour occurs when 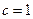, for then the sequence is 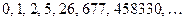; this also happens when 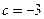, the sequence being 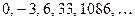; and also when 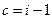, the sequence being

.

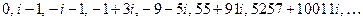The Mandelbrot set, that is to say, the black region of our world of Tor'Bled-Nam, is precisely that region of the Argand plane consisting of points 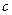for which the sequence remains bounded. The white region consists of thoses points с for which the sequence is unbounded. The detailed pictures that we saw earlier were all drawn from the outputs of computers. The computer would systematically run through possible choices of the complex number c, where for each choice of с it would work out the sequence 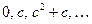and decide, according to some appropriate criterion, whether the sequence is remaining bounded or not. If it is bounded, then the computer would arrange that a black spot appear on the screen at the point corresponding to с. If it is unbounded, then the computer would arrange for a white spot. Eventually, for every pixel in the range under consideration, the decision would be made by the computer as to whether the point would be coloured white or black.

The complexity of the Mandelbrot set is very remarkable, particularly in view of the fact that the definition of this set is, as mathematical definitions go, a strikingly simple one. It is also the case that the general structure of this set is not very sensitive to the precise algebraic form of the mapping 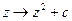that we have chosen. Many other iterated complex mappings (e.g. 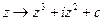) will give extraordinarily similar structures (provided that we choose an appropriate number to start with – perhaps not 0, but a number whose value is characterized by a clear mathematical rule for each appropriate choice of mapping). There is, indeed, a kind of universal or absolute character to these 'Mandelbrot' structures, with regard to iterated complex maps. The study of such structures is a subject on its own, within mathema­tics, which is referred to as complex dynamical systems.

Читайте також:

1. B. Complex Sentence
2. Look through the text and find Complex Sentences. Translate them into Ukrainian.
3. Mathematical Symbols and Signs
4. Task XX. Render the following in English. Use the Complex Object.
5. The essence of the accounting
6. Toward Mathematical Structure
7. Wording Mathematical Formulae
8. Ключове слово abstract

Переглядів: 654