
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Wording Mathematical Formulae
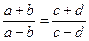 ,
,
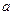 plus
plus 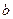 over
over 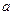 minus
minus 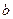 is equal to
is equal to 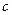 plus
plus 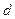 over
over 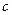 minus
minus 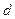 .
.
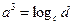 ,
,
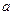 cubed is equal to the logarithm of
cubed is equal to the logarithm of 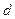 to the base
to the base 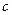 .
.
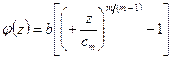 ,
,
a)  of
of  is equal to
is equal to 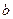 , square brackets, parenthesis,
, square brackets, parenthesis, 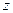 divided by
divided by 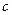 sub
sub 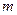 plus 2, close parenthesis, to the power
plus 2, close parenthesis, to the power 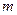 over
over 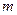 minus 1, minus 1, close square brackets;
minus 1, minus 1, close square brackets;
b) 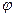 of
of 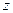 is equal to
is equal to 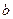 multiplied by the whole quantity: the quantity two plus
multiplied by the whole quantity: the quantity two plus 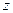 over
over 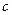 sub
sub 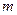 , to the power
, to the power 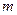 over
over 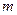 minus 1, minus 1.
minus 1, minus 1.
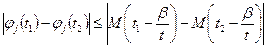 ,
,
the absolute value of the quantity 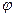 sub
sub 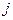 of
of 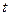 one, minus
one, minus 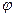 sub
sub 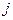 of
of 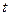 two, is less than or equal to the absolute value of the quantity
two, is less than or equal to the absolute value of the quantity 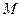 of
of 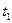 minus
minus 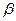 over
over 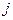 , minus
, minus 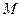 of
of 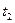 minus
minus 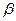 over
over 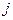 .
.
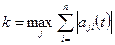
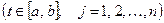 ,
,
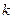 is equal to the maximum over
is equal to the maximum over 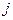 of the sum from
of the sum from 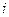 equals one to
equals one to 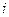 equals
equals 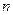 of the modulus of
of the modulus of 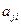 of
of 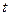 , where
, where 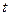 lies in the closed interval
lies in the closed interval 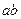 and where
and where 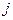 runs from one to
runs from one to 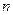 .
.
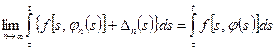 ,
,
the limit as 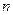 becomes infinite of the integral of
becomes infinite of the integral of 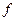 of
of  and
and 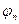 of
of  plus delta
plus delta 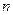 of
of  , with respect to
, with respect to  , from
, from 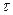 to
to 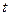 , is equal to the integral of
, is equal to the integral of 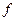 of
of  and
and 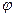 of
of  with respect to
with respect to  , from
, from 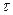 to
to 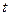 .
.
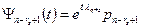
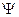 sub
sub 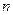 minus
minus 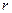 sub
sub  plus 1 of
plus 1 of 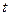 is equal to
is equal to 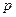 sub
sub 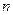 minus
minus 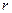 sub
sub  plus 1, times
plus 1, times 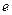 to the power
to the power 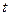 times
times 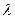 sub
sub 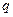 plus
plus  .
.
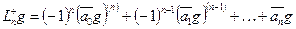 ,
,
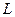

 sub
sub 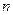 adjoint of
adjoint of 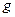 is equal to minus 1 to the
is equal to minus 1 to the 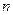 , times the
, times the 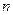 th derivative of
th derivative of 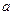 sub zero conjugate times
sub zero conjugate times 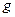 , plus, minus one to the
, plus, minus one to the 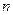 minus 1, times the
minus 1, times the 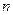 minus first derivative of
minus first derivative of 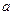 sub one conjugate times
sub one conjugate times 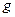 , plus … plus
, plus … plus 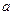 sub
sub 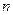 conjugate times
conjugate times 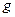 .
.
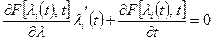 ,
,
the partial derivative of 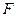 oflambda sub
oflambda sub 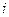 of
of 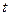 and
and 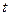 , with respect to lambda, multiplied by lambda sub
, with respect to lambda, multiplied by lambda sub 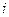 prime of
prime of 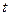 , plus the partial derivative of
, plus the partial derivative of 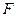 with arguments lambda sub
with arguments lambda sub 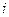 of
of 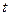 and
and 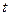 , with respect to
, with respect to 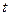 , is equal to 0.
, is equal to 0.
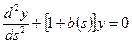 ,
,
the second derivative of 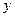 with respect to
with respect to  , plus
, plus 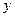 , times the quantity 1 plus
, times the quantity 1 plus 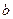 of
of  , is equal to zero.
, is equal to zero.

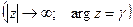 ,
,
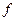 of
of 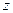 is equal to
is equal to 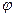 sub
sub 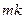 hut, plus big
hut, plus big 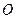 of one over the absolute value of
of one over the absolute value of 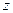 , as absolute
, as absolute 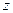 becomes infinite, with the argument of
becomes infinite, with the argument of 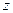 equal to gamma.
equal to gamma.
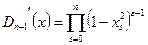 ,
,
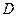 sub
sub 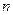 minus 1 prime of
minus 1 prime of 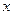 is equal to the product from
is equal to the product from  equal to zero to
equal to zero to 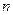 of, parenthesis, 1 minus
of, parenthesis, 1 minus 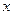 sub
sub  squared, close parenthesis, to the power … epsilon minus 1.
squared, close parenthesis, to the power … epsilon minus 1.
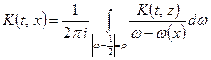 ,
,
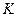 of
of 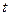 and
and 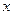 is equal to one over two
is equal to one over two 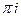 , times the integral of
, times the integral of 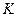 of
of 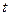 and
and 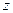 , over
, over 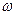 minus
minus 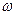 of
of 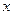 , with respect to
, with respect to 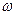 along curve of the modulus of
along curve of the modulus of 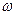 minus one half, is equal to rho.
minus one half, is equal to rho.
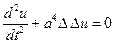
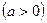 ,
,
the second partial (derivative) of 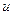 with respect to
with respect to 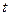 , plus
, plus 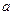 to the fourth power, times the Laplacian of the Laplacian of
to the fourth power, times the Laplacian of the Laplacian of 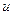 , is equal to zero, where
, is equal to zero, where 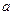 is positive.
is positive.
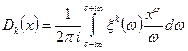
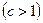 ,
,
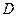 sub
sub 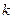 of
of 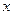 is equal to one over two
is equal to one over two 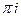 , times integral from
, times integral from 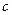 minus
minus 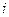 infinity to
infinity to 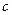 plus
plus 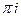 infinity of dzeta to the
infinity of dzeta to the 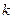 of
of 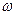 ,
, 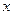 to the
to the 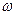 divided by
divided by 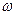 , with respect to
, with respect to 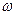 , where
, where 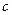 is greater than 1.
is greater than 1.
Читайте також:
- Mathematical Symbols and Signs
- Toward Mathematical Structure
- What is the very essence of mathematical visualization? Key-words: magnification, abstract mathematics, complex numbers, miracles of mathematics.
Переглядів: 610
| <== попередня сторінка | | | наступна сторінка ==> |
| Mathematical Symbols and Signs | | | Giving an Oral Presentation |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |