Toward Mathematical Structure

Three new approaches to numbers, in 1801 and in the 1830s, were to the hint at the general concept of math structure and reveal unsuspected horizons in the whole of maths. That of 1801 was the concept of congruence, introduced by Gauss. To this and the revolutionary work (1830) of E. Galois in the theory of algebraic equations can be traced the partial execution of L. Kronecker's (1823-1891) programme in the 1880s for basing all maths on the natural numbers.

The same sources are one origin of the modern abstract development of algebraic and geometric theories, in which the structure of math systems is the subject of investigation, and it is sought to obtain the interrelations of the math objectsconcerned with a minimum of calculation. "Structure" may be thought of at present in any of its intuitive meanings; it was precisely defined in 1910 by themath logicians. We shall approach math structure through the union effected In the nineteenth century between algebra and arithmetic.

From the standpoint of maths as a whole, the methodology of deliberate generalization and abstraction, culminating in the twentieth century in a rapidly growing maths of structure, is doubtless the most significant contribution of all the successive attempts to extend the number concept. But at every stage of the progression from the natural numbers 1, 2, 3, ... to other types of numbers, each оf several fields of maths adjacent to arithmetic was broadened and enriched.

New acquisitions in other fields reacted reciprocally on arithmetic. For example, the first satisfactory theory of ordinary complex numbers to become widely known was that of Gauss (1831) devised to provide a concise solution for a special problem in Diophantine analysis.

The theory of complex numbers necessitated a radical revision and generalization of the concept of arithmetical divisibility, which in turn suggested a reformulation of certain parts of algebraic geometry. The latter, in its turn, was partly responsible for further generalizations (modular systems) in the algebraic arithmetic – or arithmetical algebra – of the twentieth century. The forward movement was universal and each major advance in one department induced progress in others.

The passage to final abstractness took about a quarter of a century. The turning point was Hilbert's work on the foundation of geometry in 1899. Although this did not concern algebra or arithmetic directly, it set a new and high standard of definiteness and completeness in the statement of all math definitions or, what is equivalent, in the construction of postulate systems. A general theory of structure was developed by A. N. Whitehead and B. Russell in 1910.

It will suffice here to recall a cardinal definition: A relation 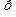between the members of a set 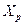has the same structure as a relation 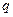between the members of a set 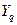if there is a one-to-one correspondence between the elements of 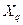and 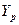such that, whenever two elements of 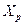are in the relation p to each other, their correlates (by the correspondence) in 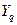are in the relation 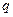to each other, and vice versa. Modern developments of numbers and their influence on the emergence of structure, the greatly generalized concept of whole number, or integer, distinguished the higher arithmetic of the late nineteenth century from all that had preceded it.

There are six major developments in maths that greatly influenced the modern theory of numbers. They are: 1) the definition by Gauss, Kummer and Dedekind of algebraic integers; 2) the restoration of the fundamental theorem of arithmetic in algebraic number fields by Dedekind's introduction of ideals; 3) the definitive work of Galois on the solution of algebraic equations by radicals; 4) the theory of finite groups; 5) the modern theory of fields that followed; 6) the partial application of arithmetical concepts to certain linear algebras.

All of these developments are closely interrelated. The last marks the farthest extension of classical arithmetic up to 1945, and it is either the climax or the beginning of a structural arithmetization of algebra, foreseen as early as 1860 by Kronecker. As if in preparation for the climax, the algebra of hypercomplex numbers rapidly outgrew its classificatory adolescence of the 1870s and became progressively more concerned with general methods reaching a certain maturity early in the twentieth century.

The fifth major development, which logically would seem to be a necessary prelude to the others, strangely enough came last. Not until the closing years of the nineteenth century was anyone greatly perturbed about the natural numbers 1, 2, 3,.... All maths, from the classical arithmetic to Fermat, Euler, Lagrange, Legendre, Gauss and their numerous imitators, to geometry and analysis, had accepted these speciously simple numbers as "given". Without them, none of the major advances of modern arithmetic would ever have happened.

Yet no arithmetician asked, "By whom are the natural numbers 'given'? Kronecker ascribed them to God, but this was hardly a math solution. The question arose, not in arithmetic, but in analysis. It was answered by the modern definition of cardinal and ordinal numbers. This finally united arithmetic and analysis at their common source.

The sixth and last major development in the evolution of the number concept was the application of arithmetic to the differential and integral calculus. It is a point of great interest that one of the strongest initial impulses for the final application of arithmetic to analysis came from math physics. It was gradually perceived that the cardinals and ordinals 1, 2, 3, ... demanded clarification. The arithmetic of 1,2,3,..., and with it math analysis, resigned its soul to the searching mercies of math logic.

About twenty-five centuries of struggle to understand numbers thus ended where it had begun with Pythagoras. The modern programme is his, but with a difference. Pythagoras trusted 1,2,3, ... to "explain" the Universe including maths, and the spirit animating his "explanation" was strict deductive reasoning. The natural numbers are still trusted by mathematicians and scientists in their technical maths and its applications. But math reasoning itself, vastly broadened and deepened in the twentieth century beyond the utmost ever imagined by any Greek, supplanted the natural numbers in math interest.

When, if ever, math logic shall have surmounted its obscurities, the natural numbers may be clearly seen for what they "are". But there will always remain the possibility that any unsealed range may conceal a higher just beyond, and arithmeticians will come upon many things to keep them busy and incompletely satisfied for the next five thousand years. After that, perhaps, it will not matter to anyone that 1,2,3, ... "are".

From the great mass of work that has been done since 1900 on the arithmetization of algebra – or vice versa – one should mention the study of all possible types of fields and the relations between them.

The final outcome may be roughly described as an analysis of the structure of fields with respect to their possible subfields and superfields. The next item, dating from about 1920 marks a distinct advance. It is represented by a host of mathematicians who undertook to do for an abstract ring what Dedekind has done for any ring of algebraic numbers, and to extend the Galois theory to abstract fields.

Thus, the Dedekind theory of ideals was abstracted and generalized, as was also the Galois theory. The first of these may properly be assigned to arithmetic, as one of the chief objectives is the discovery, for any ring, of unique decomposition theorems analogous to the fundamental theorem of arithmetic, or to the unique representation of a Dedekind ideal as a product of prime ideals.

Two basic but rather inconspicuous-looking items of the classical theory of algebraic number ideals passed unchanged into the abstract theory, "the greatest common divisor (the GCD)" and "least common multiple (LCM)". Although at the first glance these are mere details, experience has shown that they are the framework of much algebraic structure and that, when their simplest properties are restated abstractly as postulates, the resulting system unifies widely separated and apparently distinct theories of algebra and arithmetic. They lead, in fact, to what seemed the most important theory of algebraic-arithmetic structures.

The rapid expansion of the theory of structures or lattices following Dedekind's introduction of dual groups is typical of much in the recent development of maths.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Real Numbers	\|	Structures

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.