Structures

The generic concept of structure may be quite simply explained, as J. Diendonne did, namely: "If the temperature is 80⁰ F and a 20-degree rise is predicted, we expect without counting, an eventual temperature of 100⁰. If we have a book open at page 80 and we are told to look 20 pages further on, we turn without hesitation to page 100 without counting the intervening pages. We are using the fact that the structure of addition applies to both cases, adding the numbers gives the correct result when interpreted either for temperatures or for pages. We do not (fortunately!) have to learn a special arithmetic for thermometers and another for books...".

This is, of course, one of the simplest examples of structures, but it shows at once that the most striking feature of structures has something to do with the economy of thought and this aspect is naturally of paramount importance in maths. The structures are almost custom-made tools for mathematicians. Whenever a mathematician has been able to prove that the objects he is studying verify the axioms of a certain type of structure, he has ipso facto (by the fact itself) proved all the theorems from the theory of that type of structure for these particular objects (theorems which he would otherwise probably either miss altogether or for which he would have to devise special proofs).

Simularly, whenever two given structures are proved to be isomorphic, thenumber of theorems is immediately doubled, each theorem proved for one of the structures giving at once a corresponding theorem for the other (and sometimes I it is much easier to prove one than the other). No wonder, therefore, that there existwhole theories of a highly complex and difficult nature, such as the so-called "class-field theory" in the theory of numbers, whose major aim is to prove that the two structures are isomorphic.

Anyone who is familiar with the theory of groups however elementary, already knows something about the working mechanism of such structures in concrete, although he may not be explicitly aware of it. Namely, the nature of the objects or elements forming a group may vary, indeed, tremendously, but they share the same structure of group, defined by the groups themselves. If he knows, in addition, something about isomorphisms among groups, he is then even better off, since the concept of "isomorphism" is, evidently, one of those abstract notions which are closely and naturally linked to that of structure.

Generally, a structure of a certain type is defined for a set 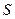if a relation between the elements of 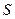is specifically defined such that a fixed set of axioms characteristic of the type of structure at issue can be verified. 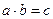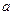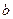For example, the structure of the group (or ring, or field, etc.) belongs to a specific type, called algebraic structures, which in turn are characterized by the prescription for composition, namely, the unique relation for any three elements 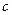.For example, addition of numbers is a prescription in virtue of which a third number is uniquely assigned to the sum of the first two; similarly, multiplication of numbers, addition of vectors, composition of rotations, etc., exemplify algebraic structures. Some algebraic structures belong to the second type, called structures of order; for example, the set of real numbers is ordered, since one of any two distinct real numbers is greater than the other.

Then again, there is the third type, called topological structures (or topologies). A topology is given on a set if a concept of neighbourhood or limit which satisfied certain conditions (also called axioms) is adopted for the set in a suitable manner. It yields, therefore, an abstract formulation of the more or less intuitive notion of neighbourhood (or limit of continuity) to which we were originally led by our physical sense of space.

The degree of abstraction necessary for the formulation of the axioms of a topology is evidently greater than that for algebraic or order structures; but this may be considered still simple or less sophisticated in comparison with certain structures which are found strung-together, namely, mixed (or multiple) structures. For example, a structure may be both algebraic and topological, linked together by new axioms, topological algebra and algebraic topology are two specific examples of such a mixed structure (although homological algebra is still unmixed, exemplifying a pure type of structure).

The mixed structure may appear also in elementary cases; for instance, the set of real numbers reveals three kinds of structures at the same time: an algebraic structure defined by computative operations (addition and multiplication), a structure of order by which inequalities between real numbers can be treated, and, finally, a topological structure where a concept of limit is explicated. These structures are obviously associated with each other so that topology may be defined by order or relations (two inequalities added term by term, etc. may exist between order and algebra). Several other structures appear strung-together, more likely at the level of advanced examples such as topological groups, differential manifolds, analytic fibre spaces, discontinuous groups of transformations, etc.

These structures, pure or mixed, are now found everywhere at the concentric centre of the math universe. A considerable diversity can be observed among the greattypes of structures, some of which may be called mother structures, namely, the most general structures with the smallest number of axioms, while there are also those which are obtainable by adding more axioms such that they will yield the harvest of new consequences. Here appear, thus, a hierarchy of structures, descending from thesimple and general at the top to the complex and particular at the bottom.

Farther along, at the lowest of the structural totem pole, one finally descends upon the ground of the particular and individual where certain areas have long remained or will for some time remain indeterminate, structure-wise, such that the "classical" maths begins to emerge. For example, certain fragments from the theory of numbers, of functions of a real or complex variable, of differential equations, of differential geometry, etc.

Nevertheless, after the extensive reconstructions even the hard-core areas cannot but fail to retain their former autonomy; they have become crossroads, where several more general structures meet and react upon each other. For example, the redoubtable theory of primes is now a close neighbour of the theory of algebraic curves, and the most ancient Euclidean geometry borders on a brand-new theory of integral equations. One cannot hope to have a complete and final list of such types of structures on hand; several new ones have been discovered, and we have every reason to expect new discoveries of that kind.

Still, there are many large chunks of classical material, where the structural reconstruction by the axiomatic method has rather very slowly progressed. This means only a greater challenge, or a new area to bulldoze through, revealing new types of structures which will introduce new fusions among theories. And these breakthroughs will, in turn, mean another substantial progress in the direction of pregnant abstraction, simplification and unification, the process of which will be adapted time and again as long as maths willgo on growing.

Читайте також:

Text 4. From the History of Architectural Structures

<== попередня сторінка	\|	наступна сторінка ==>
Toward Mathematical Structure	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.