Real Numbers

Every measurement of quantities implies a vague notion of real numbers. From (the math point of view, the origins of the theory of real numbers can be traced back to the progressive formation by the Babylonians of a system of numeration which was (in principle) capable of representing arbitrarily close approximations to any real number. The possession of such a system, and the confidence in numerical calculation which naturally resulted from it, inevitably led to a "naive" notion of real number which differs hardly at all from that which is current today (linked with the decimal system of numeration) in elementary education and among physicists and engineers.

This notion cannot be precisely defined, but can be expressed by saying that a number is regarded as defined by the possibility of finding approximations to it and using these approximations in calculation; this necessarily implies a certain amount of confusion between measures of physical quantities, which, of course, are not susceptible to an infinite series of successively closer and closer approximation, and "numbers" such as 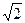(assuming that one in possession of an algorithm which would make possible an infinite series of successively closer and closer approximation of such numbers).

A similar "pragmatic" attitude appears in all math schools in which experience in calculation is more important than rigour and theory. The latter, however, were predominant in Greek maths and it is to the Greeks that we owe the first rigorous and coherent theory of ratios of magnitudes, that is, essentially, of real numbers. This theory was the culmination of a series of discoveries about proportions and, in particular, incommensurable ratios, whose importance in the history of Greek thought can hardly be exaggerated, but which in the absence of accurate texts can be discerned only in outline.

Greek maths in its early stages was inextricably bounded up with speculations, part scientific and part philosophical and mystical, about proportion, similitude and ratios, especially "simple ratios" (expressible by fractions with small numerators and denominators) and one of the characteristic tendencies of the Pythagorean school was to attempt to explain all in terms of integers and ratios of integers.

But it was the Pythagorean school, in fact, which discovered that 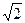is irrational. This is without doubt the first example of a proof of impossibility in maths and the mere fact of posing such a question implies a clear distinction between a ratio and approximations to it, and indicates the immense gap which separates the Greek maths from their predecessors.

We know little about the movement of ideas which accompanied and followed) this important discovery. We shall give only a brief summary of the main ideas 'which lie at the base of the theory' of ratios of magnitudes which was constructed by the great mathematician Eudoxus (a contemporary and friend of Plato), definitely adopted by classical Greek maths and is known to us through Euclid's Elements.

1) The word and the idea of number are strictly reserved to natural integers 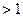(1 is the monad and not, strictly speaking, a number), to the exclusion not only of our irrational numbers but also of what we call rational numbers: to the Greek mathematicians of the classical period the latter are ratios of numbers. There is much more here than a simple question of terminology: the word "number" was for the Greeks (and for the moderns up to a recent time) linked with the idea of a system with two laws of composition (addition and multiplication); ratios of integers were regarded by the classical Greek mathematicians as operators, defined on the set of integers or on some subset of this set [the ratio of 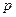to 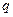is the operator, which, applied to 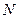, if 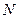is a multiple of 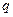, gives the integer 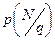forming a multiplicative group but not a system with two laws of composition].

In this the Greek mathematicians separated themselves voluntarily from the "logisticians" or professional calculators who, like their Egyptian and Babylonian predecessors, had no scruples about treating fractions as if they were numbers, or adding a fraction to an integer. It seems moreover that this self-imposed restriction on the concept of number came from philosophical rather than math motives and followed the reflections of the first Greek thinkers on the unit and the multiple, the unit (in this system of thought) being incapable of subdivision without thereby losing its character of unit.

2) The theory of magnitudes is based on axioms, which applied simultaneously to all types of magnitudes (there are allusions to earlier theories which apparently treated lengths, areas, volumes, times, etc., all separately). Magnitudes of the same type are characterized by the facts that they can be compared (that is to say, it is assumed that equality, which is an equivalence relation, and the relations 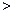and 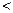are defined), that they can be added and subtracted ( 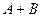is defined, and also is if 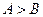) and that they satisfy "Archimedes' axiom". It is clearly realized from the beginning that this latter fact is the key stone of the whole edifice (it is, in fact, indispensable in any axiomatic characterization of real numbers).

For Eudoxus, the magnitudes of a given type form a system with one internal law of composition (addition), but that this system has an external law of composition whose operators are ratios of magnitudes, conceived of as forming an Abelian multiplicative group. The universal domain of operators thus constructed was the equivalent, for the Greek mathematicians, of what the set of real numbers is for us; moreover, it is clear that, with addition of magnitudes and multiplication of ratios of magnitudes they possessed the equivalent of what the field of real numbers is for us, although in a much less manageable form.

Such was the state of the theory of real numbers in the classical period of Greek maths. Admirable though Eudoxus' construction was, and leaving nothing to the desired in rigour or coherence, nevertheless, it must be admitted that it lacked flexibility and did not encourage the development of numerical calculation, still less the development of algebraic calculation. Moreover, its logical necessity could not be apparent except to those in love with rigour and familiar with abstraction; thus, it is natural that, with the decline of Greek maths, the "naive" point of view, which had been preserved through the tradition of the logisticians, should gradually re-emerge.

This point of view is dominant, for example, in Diophantus who in truth was an upholder of this tradition rather than of official Greek science. He reproduces the Euclidean definition of number, but in reality he used the word "number" to mean the unknown in algebraic problems whose solution may be either an integer, or a fraction, or an irrational number. Although this change of attitude on the subject of number is connected with the development of algebra, it does not, of course, constitute an advance in itself, but rather a retreat.

We cannot trace the vicissitudes of the concept of number through Hindu, Arab, and western maths up to the end of the Middle Ages. The "naive" notion of number predominated, and although Euclid's Elements served as a basis for the teaching of maths during this period, it is most likely that the doctrine of Eudoxus remained generally uncomprehended because the need for it was no longer appreciated. The "ratios" of Euclid were customarily described as "numbers", and the rules for calculating with integers were applied to them without any attempt to analyse the reasons for the success of these methods.

Nevertheless, we see R. Bombelli, as early as the middle of the 16^thcentury, expounding a point of view on this subject in his Algebra which is essentially correct; having realized that once the unit of length has been chosen, there is a one-to-one correspondence between lengths and ratios of magnitudes, he defines the various algebraic operations on lengths (assuming, of course, that the unit has been fixed) and, representing numbers by lengths, obtains the geometrical definition of the field of real numbers and thus gives his algebra a solid geometrical foundation.

In the following two centuries the definitive establishment of correct methods was twice retarded by the development of two theories: the infinitesimal calculus and the theory of series. In the seventeenth century the main subject of debate was the notion of "infinitely" small, which though justified a posteriori by the results which were obtained with its help, seemed to be in open opposition to the axiom of Archimedes; and we see the most enlightened minds of this period finally adopting a point of view which differed little from that of Bombelli, and which is distinguished above all by the greater attention it paid to the rigorous methods of the ancients.

Isaac Barrow (Newton's teacher, who himself played an important part in the creation of the infinitesimal calculus) recognized the need to return to the theory of Eudoxus in order to regain the proverbial "geometrical certainty" in the subject of number. On the other hand, defining numbers to be symbols which denote ratios of magnitudes and to be capable of being combined by the operations of arithmetic, Barrow obtains the field of real numbers in terms which Newton took up again in his Arithmetic and which his successors up to Dedekind and Cantor did not change.

But it was in this period that the method of expansion in series was introduced; this rapidly took on an extremely formal character in the hands of impenitent algebraists and deflected the attention of mathematicians from the questions of convergence which are essential to any sound use of series in the domain of real numbers. At the same time began the movement of ideas which led to the definition of continuous functions and the general definition of compact spaces. Weierstrass had perceived the logical importance in making the idea of real numbers entirely independent of the theory of magnitudes; the latter is effectively equivalent to an axiomatic definition of the points of the line (and thus of the set of real numbers) and the assumption of the existence of such a set. Although this method is essentially correct, it is evidently preferable to start only from the rational numbers, and to construct the real numbers from them by completion. This was achieved, by diverse methods and independently of each other, by Weierstrass, Dedekind, Meray and Cantor; while the method of "cuts", proposed by Dedekind came very near to the definitions of Eudoxus.

Simultaneously, Cantor began to develop the theory of sets of real numbers, the idea of which was first conceived by Dedekind, and thus obtained the principal elementary results on the topology of the real line, the structure of its open and closed sets, the notion of derived set and of totally disconnected perfect set. Cantor also obtained Theorem I on the power of the continuum and deduced from it that thecontinuum is uncountable, that the set of transcendental numbers has the power of the continuum, and also (a paradoxical result for its time) that the set of points of a plane (or of space) has the same power as the set of points of a line. With Cantor these questions assumed practically their definitive form.

Apart from leading to work on general topology and applications to integration Cantor's work has led to investigations of the structure and classification of sets of points on a line, and a realvalued functions of a real variable. These have theirorigin in the work of Borel which was directed mainly towards measure theoryand "Borel sets".

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Natural Numbers	\|	Toward Mathematical Structure

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.008 сек.