Natural Numbers

What are natural numbers? The question has been a topic of debate among philosophers and mathematicians at least since the time of Pythagoras in the sixth century B.C. Pythagoras believed that what we call the positive integers or natural numbers (1,2,3 and so on) were God-given entities that formed the ultimate foundation both of maths and of the Universe. The Pythagoreans' own discovery of such "incommensurable" quantities as the ratio between the diameter of a circle and its circumference ultimately dispelled the belief that the Universe was built on natural numbers. That the natural numbers provided the foundation of maths, however, persisted as an article of faith among mathematicians until well into the 19^th century.

But then the attitude toward the natural numbers had begun to change. The centrality of natural numbers was no longer considered an accepted fact but was viewed as a conjecture that required rigorous proof. The proofs usually took the form of a stepwise derivation of such well-known number systems as rational, real and complex numbers from the natural numbers themselves. Two examples are the attempts of K.Weierstrass and R. Dedekind to "arithmetize" math analysis. Both scholars derived real numbers – the combined set of all rational and irrational numbers that is employed in most classical maths – from the rational numbers. A third example is the proposal of L.Kronecker to found all maths on the natural numbers. This Kronecker attempted to accomplish solely with "finitary" methods, that is, methods invoking neither nonfinite entities nor proofs involving more than a finite number of steps.

Still other mathematicians, in particular those who were conversant with contemporary advances in symbolic logic, put forward the suggestion that, far from being God-given, natural numbers were constructions of the human mind. The three most famous propagators of this suggestion were G.Frege, G.Peano and B.Russell. Obviously a theory was needed that would trace the rise of the natural numbers from some more basic notion or notions, but how was such a theory to be constructed? If most or all of classical maths had evolved from the natural numbers, it was improbable that the required theory could be devised entirely within the bounds of classical maths.

First Frege, then Peano and finally Russell turned to symbolic logic as a potential source of the fundamental notions necessary for a theory of natural numbers. Frege was the first of the three to publish specific theory (1884) in which he proposed that the natural numbers could be reduced to the notion of "class" and the operation of "correspondence", by virtue of which classes are quantified. According to Frege, each natural number 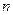was to be regarded as a "superordinate class" whose members, "subordinate classes", each contain precisely n elements. Given two subordinate classes, A and B, the two are said to be members of the same superordinate class, that is, instances of the same number, if and only if a one-to-one correspondence can be established between their respective elements. If instead the correspondence is many to one, then A and В are said to be instances of different numbers.

In essence, Frege's theory states that the series of natural numbers presents a general problem of quantification, but that the general problem can be reduced to the more restricted notion of "cardination" or quantifying classes. The commonest example of cardination is the matching of things. Frege's cardinal theory remained unknown until Russell rediscovered it in 1901. Russell subsequently published the cardinal theory, with full acknowledgement to Frege, in his own works and in his joint work with A.N. Whitehead: Principia Mathematica (1910-1913).

Between the time Frege first published the cardinal theory and the time Russell rediscovered it, Peano developed a second theory about the natural numbers. This theory first appeared in 1894 in the form of five axioms, that we shall slightly reword here. First, 1 is a natural number. Second, any number that is the successor of a natural number is itself a natural number. Third, no two natural numbers have the same successor. Fourth, the natural number 1 is not the successor of any natural number. Fifth, if a series of natural numbers include both the number 1 and the successor of every natural number, then the series contains all natural numbers.

In essence, Peano's theory places the natural numbers in an ordinal relation or in the language of symbolic logic, a "transitive, asymmetrical relation". If we are willing to stipulate that the relation R that obtains between every nonidentical pair of natural numbers be an ordinal relation, then the complete series of natural numbers can be constructed stepwise with the aid of the rule of math induction. Like Frege's cardinal theory, Peano's states that the series of natural numbers presents a general problem of quantification. Unlike Frege's theory, however, Peano's ordinal theory reduces the general problem to the more restricted notion of quantifying transitive, asymmetrical relations, or ordination. The commonest example of ordination is the counting of things.

Just which of the two theories, the cardinal or the ordinal, is mathematically preferable is a question that has never been answered to everyone's satisfaction. Reasonable objections can be lodged against both. For example, the cardinal theory is subject to the celebrated paradox, discovered by Russell in 1901, concerning the class composed of all those classes that are not members of themselves. With respect to the ordinal theory, as Russell pointed out, whereas Peano's five axioms obviously are satisfied by the series of natural numbers, they are equally satisfied by other number systems. For example, the rational fractions (1, , , 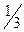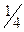and so on) satisfy the axioms, as will any series of math or empirical entities that has a beginning, no repetitions and no end and is such that every entity can be reached in a finite number of steps. In short,, the domain of application of the ordinal theory is much wider than the series of natural numbers.

Because there is no universally accepted math basis for choosing between the cardinal and the ordinal theories, the choice becomes a subjective matter. Typically, the choice is determined by one's degree of sympathy with one or another of three modern schools of math thought: logicism, formalism and intuitionism. Those who lean toward logicism, favour the cardinal theory, a choice that is natural enough when one considers that the codiscoverers of the theory, Frege and Russell, were the principal founders of logicism. Those whose sympathies are with formalism, lean toward the ordinal theory; the fact that Peano's axioms seem to denude the number concept of innate "meaning" probably explains this preference. As for the intuitionists, they have, in effect, returned to the Pythagorean position that the natural numbers must be accepted without further analysis as the foundation of maths. They deny that the natural numbers are the invention of math minds and offer a "psychological" thesis: The series of natural numbers is an innate intuition, present at birth in all normal members of the human species.

Nonmath scholars tend to view with profound indifference the tortures that mathematicians suffer over such basic issues as the nature of number. They have learned from centuries of hard experience that the mere fact that the foundations of some math system or concept are not secure need not deter them from employing the system in their work. On the contrary, math notions whose foundations have been matters of continuous debate have often yielded the most mileage; the notion of an infinitesimal is perhaps the best-known example. Unlike the infinitesimal, number is not the exclusive property, or even, largely, the personal property, of the mathematician. Number has been a concept of social importance since the dawn of recorded history. The significance to society of number and number-related skills has increased tremendously with the rise of industrial civilization.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
The Greek Genius	\|	Real Numbers

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.012 сек.