The Greek Genius

"The Greek genius" did not happen spontaneously. Once the Greeks were settled in the Peloponesus and on the western shores of Asia Minor, they began to travel. Soon they were off the faraway places. On these travels they made contact with many more ancient cultures – in India, in Mesopotamia, and in Egypt. They learned and partially absorbed ways of life that had taken thousands of years to develop. Knowledge, wisdom and religion often were indistinguishable in these ancient cultures. What the early Greek travellers brought home from their trips abroad was a curious and intricate mixture of various religious cults and philosophies of life grown under conditions very different from those familiar to the Greeks. They accumulated also a tremendous wealth of knowledge pertaining to practically all aspects of life. Deeply woven into it all was knowledge of numeration and number, astronomy and (as we would call it now) astrology, and an abundance of geometric patterns and designs.

It may be supported that the early Greeks were not very much interested in numeration – if, indeed, they were interested in it at all. This was true in spite of the infinite contact with positional numeration systems, like those of Babylonians, which were vastly superior in design and manageability to their own nonpositional numeration system. Their minds apparently were not inclined toward the mechanical and rote aspects of elementary maths but rather were fascinated by suspected underlying reasons and possible justifications.

The Pythagoreans did not refine and propagandize numeration but concentrated – aside from their magnificent work in geometry – on studying the properties of numbers, in particular, the positive integers. They, thereby, missed or knowingly passed by the much more significant study of the properties of operations on numbers, which might have led them to create a structure of number systems similar to that which they created for geometry.

To appreciate the preoccupation of the Pythagoreans with properties of numbers, we must keep two things in mind: 1) The Greeks had inherited from the earlier Eastern cultures an almost inextricable mixture of genuine number knowledge, myths, religious beliefs; 2) The prevailing numeration system of this period made use of the standard Greek alphabet supplemented by special symbols so as to make a set of twenty-seven characters. Although there was no difficulty in determining when the symbols represented a number instead of a word, it was possible to use the numerical value of each letter to assign a unique number to any given word.

Regardless of what mystical reasons may have motivated the early Pythagorean investigators, they discovered many curious and fascinating number properties. Since the general Greek outlook toward maths was more geometric than in arithmetical, and since in their earlier work the Greeks considered only whole numbers, it is no wonder that they attempted to represent numbers as geometric patterns.

The Greeks' concern with prime numbers was considerably deeper and more serious. It was known that, with the exception of one and two, any whole number that is not prime can be expressed as a product of primes. The Greeks not only formalized these findings but established what later became known as "the fundamental theorem of arithmetic" – namely, that a composite number can be expressed as a product of primes in one and only one way. This theorem is known as the "unique factorization theorem". Euclid presented a proof in his Elements to show that the set of prime numbers is infinite – that is, that there is no greatestprime. In spite of many attempts so far, no one has been able to devise a practicaltest for checking the primality of large numbers, nor has a truly general prime generator been discovered.

With due respect to a very few isolated Greek mathematicians, it must be pointed out that the only numbers accepted by Greeks were the natural numbers. The foremost of these few mathematicians was Eudoxus (408-355 B.C.). He showedthat the measure of the diagonal of the unit square could not be expressed as the ratio of two natural numbers, that is, that the symbol 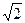does not represent a rational number. He developed an ingenious theory of "equal ratios" which with just a few minor refinements could have become the basis for the real number system. Probably, Eudoxus was not understood by more than a very few contemporaries; it is doubtful whether any of them (and this may well include Euclid himself) could have foreseen the tremendous implications of this discovery.

To most of the Greek mathematicians the very idea of incommensurable quantities was disagreeable and fearful. Eudoxus' theory of equal ratios was soon discarded and forgotten. More than two thousand years elapsed before the German mathematicians Dedekind and Cantor took up the work where Eudoxus had left off and brought it to completion creating the real number system and thereby, a legitimate "place" for imaginary and complex numbers.

Thus, the "Greek genius" was no more concerned with number systems than with numerational systems. While the math contributions of many ancient cultures were numeration, a principal Greek contribution was arithmetic, knowledge of the properties of numbers. The modern approach is definitely oriented toward the structural properties of number systems (not of numeration systems) – that is, toward the patterns and properties of operations on numbers which provide unity, simplicity, and continuity from the system of the whole numbers through the system of the complex numbers.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Active Vocabulary	\|	Natural Numbers

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.001 сек.