• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Leonhard Euler

Leonhard Euler (1707-1783) was a remarkable scientist whose contributions have left their imprint on almost all branches of maths. His papers were re­warded ten times by prizes of the French Academy. His productivity was im­mense; it has been estimated that his collected works fill upward of 100 large volumes. One of his best known works Complete Introduction to Algebra (1770) contains much material on elementary number theory. Euler's factorization method applies only to numbers which in some way can be represented as a sum of two squares 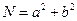as, for instance, 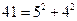. It is possible to show that if a number can be represented as the sum of two squares, one can find all factorizations by Euler's method. Euler's method is capable of wide extensions. It leads to the theory of representations of numbers by means of a quadratic forms, i.e., .

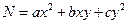Such representations can under certain conditions be used for factoring in the same manner as the special form .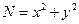

It will carry us too far to discuss the great number of other aids and methods for factoring, some of them very ingenious. Considerable effort has been centred on the factorization of numbers of particular types. Some of them are numbers resulting from math problems of interest. Others have been selected because it is known for theoretical reasons that the factors must have a special form. Among the numbers that have been examinated in great detail one should mention the so-called binomial numbers 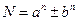where 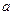and 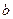are integers.

Переглядів: 478