• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Georg Friedrich Bernhard Riemann

Although Euler had begun applying the methods of the calculus to number-theory problems, however, the German mathematician G. F. B. Riemann (1826-1866) is generally regarded as the real founder of analytic number theory. His personal life was modest and uneventful until his premature death from tuberculosis. According to the wish of his father he was originally destined to become a minister, but his shyness and lack of ability as a speaker made him abandon this plan in favour of math scholarship. At present he is recognized as one of the most penetrating and original math minds of the nineteenth century. In analytic number theory, as well as in many other fields of maths, his ideas still have a profound influence.

His starting point was a function now called Riemann's zeta function

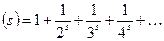
This function he investigated in great detail and showed that its properties are closely connected with the prime-number distribution. On the basis of Riemann's ideas, the prime-number theorems were proved by other mathematicians. Much progress has been made in analytic number theory since that time, but it remains a peculiar fact that the key to some of the most essential problems lies in the so-called Riemann's hypothesis, the last of his conjectures about the zeta function, which has not been demonstrated. It states that the complex roots of the func­tion all have the real component .

Переглядів: 521