• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Строк позики при механізмі складного нарахування процентів.

Перетворенням формули (2.10) знаходимо кількість періодів нарахування процентів «n». Ми знаємо, що формула (2.10) має вигляд FV=PV ·(1 + і) 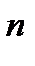. За допомогою логарифмування правої та лівої частин формули (2.10) одержуємо:

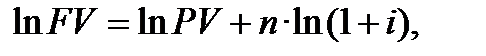або

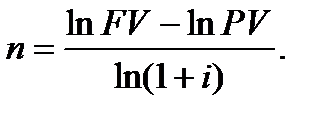
Пам’ятаючи, що різниця логарифмів двох чисел дорів­нює логарифмові частки цих чисел, одержуємо формулу для визначення строку фінансової операції для випадку складних процентів:

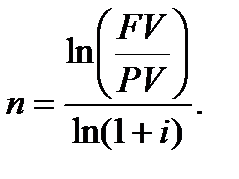(6.21)

Формулу (2.10) не обов’язково перетворювати за допомогою лише натуральних логарифмів. Можливе перетворення і за допомогою десятинних логарифмів:

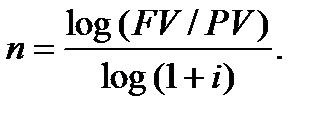(6.22)

Перетворення формули (6.2) дає такий результат:

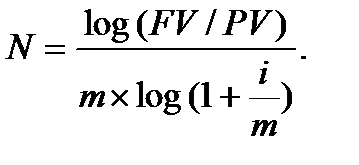(6.23)

Зазначимо, що параметр т (кількість разів нарахування процентів у році) у вигляді простої формули отриманий бути не може. Формула (6.2) відносно т являє собою так зване трансцендентне рівняння, яке можна вирішити тільки приблизно. При необхідності його розв’язування можна використовувати відповідні готові програми для комп’ю­тера.

При складному обліковому дисконтуванні, використовуючи формулу (4.5), розрахунок кількості періодів нарахування процентів має такий вигляд:

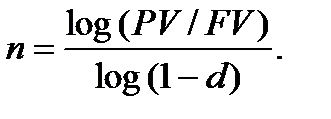(6.24)

Перетворення формули (6.4) дає такий результат:

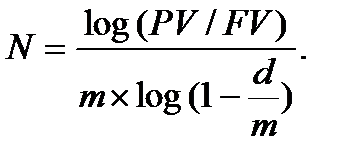(6.25)

В формулах (6.21), (6.22), (6.24) строк «n» дає результат в роках, якщо в розрахунку використовуються ставки «і» або «d» ─ річні; «n» є кількістю півріч, якщо в розрахунку використовуються ставки «і» або «d» ─ піврічні; «n» визначає кількість кварталів, якщо в розрахунку використовуються ставки «і» або «d» ─ квартальні, інші «n» визначаються відповідно.

Формули (6.23), (6.25) дають результат (строк «N») завжди в роках і в розрахунку використовуються ставки «і» або «d» ─ завжди номінальні, тобто ─ річні.

Розмір ставок процента при механізмі простого нарахування процентів.Необхідність розрахунку чисельних значень процентних ставок або облікових ставок виникає при визначенні фінансової ефективності операції або при порівнянні інвестиційних варіантів по їх доходності у випадках, коли ставки у явному вигляді не надано. Перетворюючи формули (2.2), (4.1), а також (2.5) і (4.3) відносно «і» та «d» , одержуємо відповідні формули для строків, що вимірюються роками або днями:

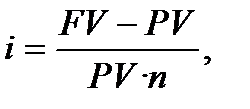або 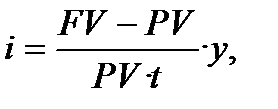(6.26)

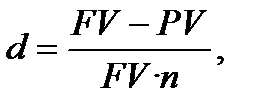або 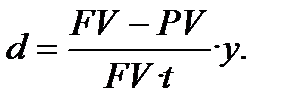(6.27)

_Додаткова інформація_________________________

Іноді розмір дисконту фіксується у вигляді процента знижки (загальної облікової ставки) « » за весь строк фінансової операції. В такому випадку 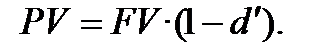Взявши до уваги, що 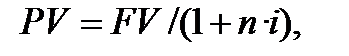знаходимо річну процентну ставку відповідну загальній обліковій « »:

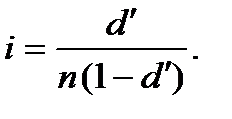
Річна облікова ставка відповідна загальній обліковій « » розраховується так:

Розмір ставок процента при механізмі складного нарахування процентів.Розрахунок чисельних значень процентних та облікових ставок при використанні механізму складного нарахування процентів одержано шляхом перетворення рівнянь (2.10), (6.2), (4.5), (6.4) відносно ставок проценту.

При нарощенні по складній процентній ставці з формул (2.10), (6.2) маємо:

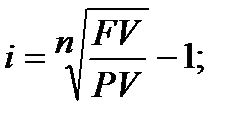(6.28)

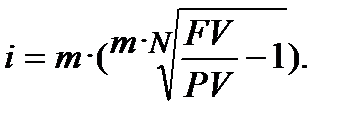(6.29)

При дисконтуванні по складній обліковій ставці з формул (4.5), (6.4) маємо:

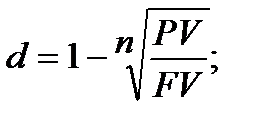(6.30)

(6.31)

Звертаємо увагу, що в формулах (6.28) та (6.30) ставка «і» або «d» є річною, якщо в розрахунку використовується «n», який показує кількість років; ставка «і» або «d» є піврічною, якщо «n» є кількістю півріч; ставка «і» або «d» є квартальною, якщо «n» визначає кількість кварталів; і далі, така ж взаємопов’язаність між «n»та ставками«і» або «d».

А у формулах (6.29), (6.31) ставка «і» або «d» завжди є річною (номінальною) тому, що строк «N» ─ це завжди кількість років, а «m», нагадуємо, кількість нарахувань у році.

_Приклад 6.5__________________________________

Читайте також:

1. Аварійне та довгострокове прогнозування хімічної обстановки
2. Адміністративна відповідальність та строки адміністративної відповідальності
3. Акти застосування норм права в механізмі правового регулювання.
4. Альтернативні варіанти довгострокового фінансування діяльності підприємства
5. Амортизація основних фондів підприємства. Методи нарахування амортизації
6. Амортизація основних фондів підприємства. Методи нарахування амортизації.
7. Амортизація основних фондів, методи її нарахування.
8. Амортизація. Методи нарахування амортизації.
9. Ануїтети з безперервним нарахуванням процентів
10. Аудит довгострокових позик і векселів
11. Аудит короткострокових кредитів і прострочених позик
12. Банківське кредитування здійснюється за такими принципами: строковість, повернення, цільовий характер, забезпеченість та платність кредиту.

Переглядів: 414