Розрахунки ануїтетів при механізмі простого нарахування процентів

При розрахунках ануїтетів на практиці частіше використовується механізм складного нарахування процентів. Але існують ануїтети з використанням механізму простого нарахування процентів. Розглянемо формули розрахунку нарощеної суми та поточної вартості в таких ануїтетах.

Розглянемо випадок коли внески здійснюються один раз в кінці року (потік постнумерандо), нарахування процентів ─ річне. В цьому випадку майбутня вартість такого ануїтету складається із суми річних внесків, кожний з яких (кожний із внесків ─ Р) збільшується на відповідну йому суму простих процентів, що на нього нараховуються. Перший внесок Р збільшується на коефіцієнт [1+(k 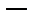1)·i], де k ─ кількість внесків Р впродовж строку дії ануїтету. Другий внесок Р збільшується на коефіцієнт [1+(k 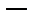2)·i], третій ─ на [1+(k 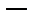3)·i] і так до розрахунку внеску Р, при якому коефіцієнт стане таким: [1+(k 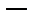k)·i], тобто, коефіцієнт стає рівним одиниці і це означає що на останній внесок Р проценти не нараховуються.

Запишемо послідовно внески наведеного ануїтету разом з відповідними кожному з них коефіцієнтами нарощення і можемо констатувати, що це ─ арифметична регресія, або арифметична прогресія ─ за умови роз-ташування внесків з коефіцієнтами у зворотному порядку.

_Додаткова інформація_________________________

Арифметичною прогресією є послідовність чисел в якій різниця між наступними та попередніми членами є незмінною. Ця незмінна різниця має назву ─ різниця прогресії. Сума k членів арифметичної прогресії 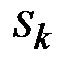розраховується за формулою:

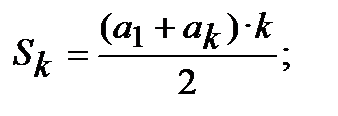(12.24)

де 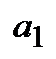─ перший член прогресії;

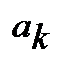─ останній член прогресії;

k ─ кількість членів прогресії.

Також, суму k членів арифметичної прогресії 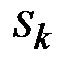можна розрахувати за формулою:

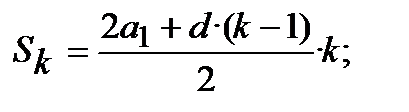(12.25)

де d ─ різниця прогресії; якщо відомі два члена арифметичної прогресії, що стоять поруч, то .

Тоді сума членів ряду платежів річного ануїтету постнумерандо розраховується за допомогою формули суми членів арифметичної прогресії (формула 12.24) де першим членом прогресії є Р, а останній член прогресії дорівнює Р·[1+ (k 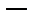1)·i]. Отже, майбутня вартість простого річного ануїтету постнумерандо розраховується за формулою:

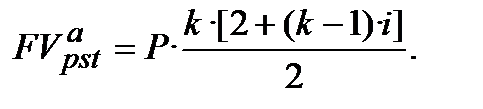(12.26)

Поточна (приведена) вартість простого річного ануїтету постнумерандо не є арифметичною прогресією, тому не може бути виведеною у вигляді компактної формули подібної до розрахунку 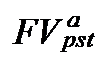─ (формула 12.26). Також, приведена вартість простого річного ануїтету постнумерандо не є також і геометричною прогресією. Приведена вартість простого річного ануїтету постнумерандо, а рівно як і пренумерандо може бути розрахована за загальною формулою розрахунку (див. формулу 12.28).

У зв’язку з тим, що формула 12.26 «спрацьовує» в умовах, за яких кількість внесків (платежів) співпадає з кількістю років, тобто k=N, то вона може мати і такий запис:

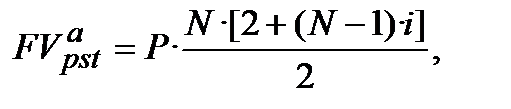(12.26*)

Цілком можливим є варіант розрахунку ануїтетів що застосовують механізм простого нарахування процентів за загальними формулами розрахунку показників FV і PV грошових потоків:

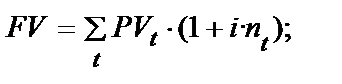(12.27)

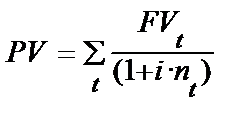. (12.28)

При внесенні платежів р-раз за рік (потік постнумерандо) з нарахуванням простих процентів один раз на рік нарощена сума ануїтету дорівнює:

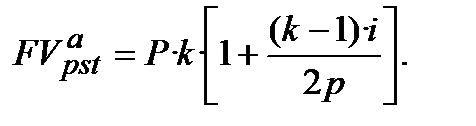(12.29)

Поточна (приведена) вартість простого річного ануїтету постнумерандо при внесенні платежів р-раз за рік розраховується за формулою (12.28), але може бути записана і по-іншому:

(12.30)

Формули 12.26 та 12.29 виведені за допомогою формули 12.24. Також і будь-які інші варіанти формул розрахунку майбутньої вартості ануїтетів при застосуванні механізму простого нарахування процентів можуть бути виведеними за допомогою формул 12.24 та 12.25.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Майбутня та теперішня вартості авансового ануїтету (ануїтету пренумерандо) при використанні облікової ставки	\|	Ануїтети з безперервним нарахуванням процентів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.