• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Гіпербола та її застосування

В ряді задач механіки зустрічається поняття гіперболи. Дуже поширене це поняття у механіці космічних польотів. Це пов’язане з запуском космічних апаратів. У сфері дії Землі траєкторія космічного апарата може бути гіперболічною.

1. Канонічне рівняння гіперболи. Гіперболою називається множина всіх точок площини, модуль різниці відстаней від кожної з яких до двох даних точок тієї ж площини, які називаються фокусами, є величина постійна, менша ніж відстань між фокусами.

Складемо рівняння гіперболи з фокусами у точках 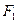і .

Для цього виберемо прямокутну систему координат так, щоб вісь проходила через фокуси гіперболи, а початок координат ділив відрізок 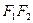пополам (рис.3.8).

Позначимо , отримаємо і . Нехай 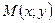– довільна точка гіперболи.

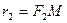Відстані і називаються фокальними радіусами точки .

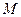За означенням гіперболи (1), де 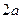– величина постійна і , тобто .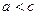

Підставивши 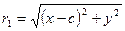і у рівність (1), отримаємо рівняння гіперболи 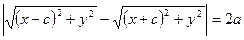. (2)

Рівняння (2) можна привести до більш простого виду:

,

,

,

,

,

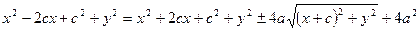тобто .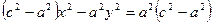

Так як 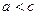, то . Покладемо 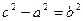(3), тоді остання рівність перепишеться у вигляді , або . (4)

Рівняння (4) називається канонічним рівнянням гіперболи.

Рівняння (4) є алгебраїчним рівнянням другого степеня. Отже, гіпербола є алгебраїчною лінією другого порядку.

2. Дослідження форми гіперболи за її рівнянням. Визначимо форму гіперболи за її канонічним рівнянням (рис.3.9):

1) Координати точки 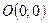не задовольняють рівняння (4), тому гіпербола не проходить через початок координат.

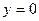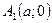2) Знайдемо точки перетину гіперболи з осями координат. Нехай у (4) , знахо-димо . Отже, гіпербо-ла перетинає вісь у точках і 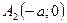. Нехай у (4) 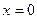, знахо-димо 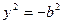, а це означає, що система не має дійсних розв’язків. Отже, гіпербола не перетинає вісь .

3) Так як у рівняння (4) змінні і 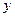входять лише у парних степенях, то гіпербола симетрична відносно осей координат, а отже, і відносно початку координат.

4) Всі точки гіперболи розташовані зліва від прямої і праворуч від прямої .

5) Гіпербола складається з двох віток, одна з яких розташована праворуч від прямої (права вітка гіперболи), а друга – ліворуч від прямої (ліва вітка гіперболи).

Точки 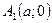і 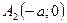перетину гіперболи з віссю називаються вершинами гіперболи.

Відрізок ( 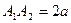), який з’єднує вершини гіперболи, називається дійсною віссю. Відрізок 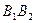( 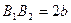), який з’єднує і , називається уявною віссю. Число називається дійсною піввіссю, число 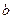– уявною піввіссю.

Вісі і 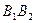є осями симетрії гіперболи. Точка 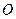перетину осей симетрії називається центром гіперболи.

У гіперболи (4) фокуси 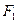і завжди знаходяться на дійсній осі.

Приклад 1. Скласти рівняння гіперболи, вершини якої знаходяться у точках 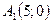і 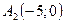, а відстань між фокусами дорівнює .

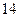Розв’язання. Маєм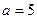о ; , тобто .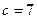

За формулою .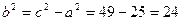

Отже, шукане рівняння .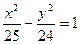

Відповідь: .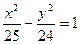

Приклад 2. Скласти канонічне рівняння гіперболи, якщо довжина її дійсної осі дорівнює 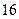і гіпербола проходить через точку .

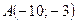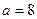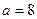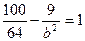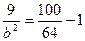Розв’язання. Маємо , тобто . Поклавши у (4) , , , отримаємо , , , , , тобто .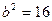

Отже, .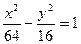

Відповідь: .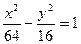

3. Асимптоти гіперболи. Рівняння асимптот гіперболи мають вигляд .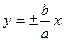

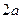Асимптоти є продовженнями діа-гоналей прямокутни-ка, сторони якого паралельні осям та і рівні відповідно і 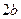, а його центр знаходиться у початку координат. При цьому вітки гіперболи розташо-вані всередині вертикальних кутів, які утворюють асимптоти, і наближаються як завгодно близько до асимптот (рис.3.10).

Приклад. Скласти рівняння гіперболи, яка проходить через точку і має асимптоти .

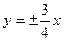Розв’язання. З даних рівнянь асимптот маємо 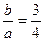, тобто 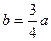. Замінивши у рівнянні гіперболи (4) змінні і 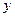координатами точки 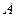і 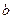його знайденим значенням, отримаємо 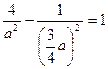, , , , звідки .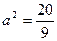

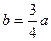, тобто .

Отже, шукане рівняння буде , або .

Відповідь: .

4. Ексцентриситет гіперболи. Ексцентриситет гіперболи називається відношення відстані між фокусами до довжини дійсної осі і позначається буквою .

(5)

Збільшення (зменшення) ексцентриситету відповідає збільшенню (зменшенню) відношенні 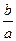. Це випливає зі співвідношення .

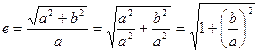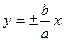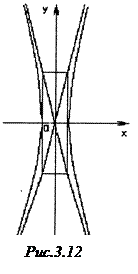Якщо ексцентриситет прямує до , залишаючись більше , то відношення (кутовий коефіцієнт асимптоти) прямує до нуля, тобто асимптоти прямують до горизонтального положення, а отже, вітки гіперболи наближаються, «притискаються» до осі (рис.3.11).

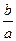Якщо ексцентриситет необмежено зростає ( ), то відношення також прямує до нескінченності, тобто асимптоти прямують до вертикального положення (до осі ), а отже, вітки гіперболи все круті-ше піднімаються догори над віссю (рис.3.12).

Приклад. Знайти ексцентриситет гіперболи .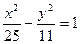

Розв’язання. З рівняння гіперболи маємо , тобто ; .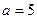

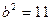За формулою (5):

.

Відповідь: .

5. Директрисигіперболи. Директрисами гіперболи називаються дві прямі, які перпендикулярні до фокальної осі (тобто до осі, на якій розміщені фокуси) гіперболи і знаходяться на відстані від центра гіперболи.

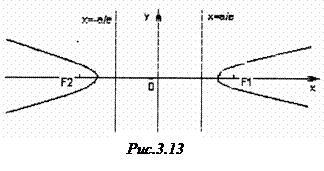Директриси гіперболи не перетинають її. Якщо фокуси гіперболи ле-жать на осі , то директриси паралельні осі (рис.3.13). Тому рівняння директрис гіперболи мають вигляд .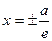

Властивість гіперболи:

Відношення довжини фокального радіуса кожної точки гіперболи до відстані 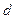цієї точки від відповідної директриси є сталим і дорівнює ексцентриситету гіперболи, тобто .

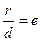Приклад. Скласти канонічне рівняння гіперболи, якщо відомі відстань між її директрисами 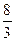і ексцентриситет .

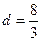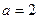Розв’язання. За умовою відстань між директрисами і . Тому маємо або , . Звідси і .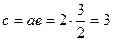

Отже, .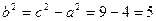

Тоді шукане рівняння гіперболи має вигляд .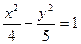

Відповідь: .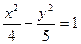

6. Спряжені гіперболи. Розглянемо рівняння виду 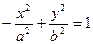(6).

При переході до нової системи координат, отриманої в результаті повороту осей старої системи навколо початку координат на кут 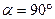(або ), рів-няння (6) пере-твориться у рів-няння гіперболи .

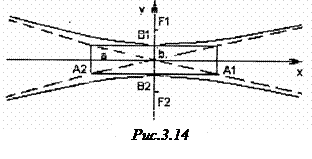
Отже, крива, яка визначається рівнянням (6) є гіпербола, дійсна вісь 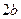якої розташована на осі , а уявна вісь 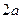– на осі (рис.3.14).

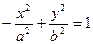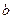Дві гіперболи, які визначаються рівняннями і в одній і тій самій системі координат і при одних і тих же значеннях і , називаються спряженими одна з одною.

7. Рівностороння гіпербола. Гіпербола називається рівносторонньою (рівнобічною), якщо довжини її півосей рівні між собою, тобто .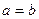

В цьому випадку рівняння гіперболи прийме вигляд 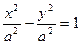, або (7).

Рівностороння гіпербола визначається одним пара-метром , її асимптотами є бісектриси координатних кутів (рис.3.15).

У всіх рівносторонніх гіпербол один і той самий ексцентриситет

.

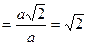Приклад. Скласти рівняння рівнобічної гіперболи, яка проходить через точку .

Розв’язання. Замінивши у (7) змінні та 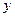координатами точки 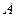, отримаємо: , тобто .

Отже, шуканим рівнянням буде .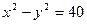

Відповідь: .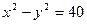

8. Рівняння гіперболи зі зміщеним центром. Якщо центр гіперболи знаходиться не в початку координат, а в точці , а осі гіперболи паралельні осям координат, то рівняння гіперболи буде мати вигляд

і . (8)

Його називають рівнянням гіперболи зі зміщеним центром.

Приклад. Встановити, чи рівняння визначає гіперболу, і знайти координати її центра, півосі і ексцентриситет.

Розв’язання. Згрупуємо члени рівняння з та 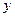і виділимо повні квадрати. Маємо

,

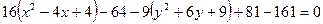або .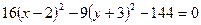

Поділимо всі члени рівняння на : 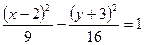– рівняння гіперболи.

Центр гіперболи знаходиться в точці , дійсна піввісь дорівнює , уявна – . Знайдемо . Тоді .

Відповідь: гіпербола; , , , .

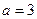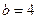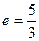Читайте також:

1. V. Виконання вправ на застосування узагальнювальних правил.
2. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
3. Автомобільні ваги із застосуванням цифрових датчиків
4. Акти застосування норм права в механізмі правового регулювання.
5. Акти застосування юридичних норм: поняття, ознаки, види.
6. Акти правозастосування, їх види
7. Акти правозастосування.
8. Алгоритм із застосування річної процентної ставки r.
9. Алгоритм із застосуванням річної облікової ставки d.
10. Аміноглікозиди (стрептоміцину сульфат, гентаміцину сульфат). Механізм і спектр протимікробної дії, застосування, побічні ефекти.
11. Аналіз зображувальних засобів. Застосування цілісного аналізу
12. Антисептики ароматичного ряду (фенол чистий, іхтіол, дьоготь, мазь Вількінсона, лінімент за Вишневським). Особливості протимікробної дії та застосування.

Переглядів: 17492