
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Парабола та її застосування
Парабола – добре відома ще зі школи.
 Так, в фізиці розглядали параболу, як траєкторію руху тіла, наприклад камінь (снаряд) кинутий під кутом до горизонту (при цьому, якщо враховувати опір повітря, то крива, що описується тілом, буде трохи відрізнятися від параболи – зображена пунктиром).
Так, в фізиці розглядали параболу, як траєкторію руху тіла, наприклад камінь (снаряд) кинутий під кутом до горизонту (при цьому, якщо враховувати опір повітря, то крива, що описується тілом, буде трохи відрізнятися від параболи – зображена пунктиром).
Поняття параболи використовується у ряді задач астрономії, архітектури. Наприклад, параболічні дзеркала; арки мостів; космічні апарати можуть рухатися по параболічній траєкторії.
1. Канонічне рівняння параболи. Параболою називається множина точок площини, кожна з яких однаково віддалена від даної точки, яка називається фокусом, і від даної прямої, що не проходе через дану точку і називається директрисою.
Складемо рівняння параболи з фокусом у даній точці 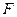 і директрисою якої є пряма
і директрисою якої є пряма 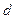 , що не проходе через
, що не проходе через 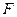 .
.
 Виберемо прямокутну систему координат так, щоб вісь
Виберемо прямокутну систему координат так, щоб вісь  була проведена через фокус
була проведена через фокус 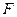 перпендикулярно директрисі
перпендикулярно директрисі 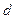 у напрямі від
у напрямі від 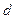 до
до 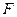 , а початок координат
, а початок координат 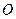 був розташований посередині між фокусом і директрисою (рис.3.16).
був розташований посередині між фокусом і директрисою (рис.3.16).
Відстань від фокуса 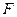 до директриси
до директриси 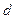 називається параметром параболи і позначається через
називається параметром параболи і позначається через 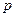 (
(  ).
).
Отже, фокус 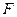 має координати
має координати 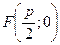 ; а рівняння директриси має вигляд
; а рівняння директриси має вигляд  , або
, або 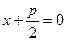 .
.
Нехай 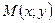 – довільна точка параболи. З’єднаємо точку
– довільна точка параболи. З’єднаємо точку 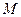 з
з 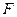 і проведемо
і проведемо 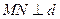 . Безпосередньо з рис.1 видно, що
. Безпосередньо з рис.1 видно, що  , а за формулою відстані між двома точками
, а за формулою відстані між двома точками 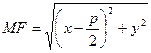 . Згідно означенню параболи
. Згідно означенню параболи 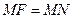 (1), отже,
(1), отже, 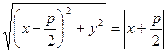 . (2)
. (2)
Рівняння (2) є шуканим рівнянням параболи. Для спрощення (2) перетворюємо його наступним чином 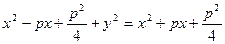 , тобто
, тобто 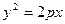 . (3)
. (3)
Рівняння (3) називається канонічним рівнянням параболи.
Рівняння (3) є алгебраїчним рівнянням другого степеня. Отже, парабола є алгебраїчною лінією другого порядку.
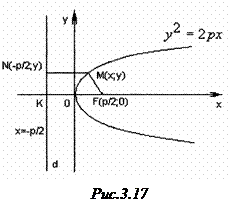 2. Дослідження форми параболи за її рівнянням. Визначимо форму параболи за її канонічним рівнянням (рис.3.17):
2. Дослідження форми параболи за її рівнянням. Визначимо форму параболи за її канонічним рівнянням (рис.3.17):
1) Координати точки 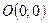 задовольняють рівнянню (3), отже, парабола, визначена цим рівнянням, проходе через початок координат.
задовольняють рівнянню (3), отже, парабола, визначена цим рівнянням, проходе через початок координат.
2) Так як у (3) змінна 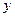 входить лише у парній степені, то парабола
входить лише у парній степені, то парабола 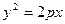 симетрична відносно осі абсцис.
симетрична відносно осі абсцис.
3) Так як  , то з (3) випливає, що
, то з (3) випливає, що 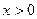 . Отже, парабола
. Отже, парабола 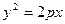 розташована праворуч від осі
розташована праворуч від осі  .
.
4) Вісі параболи необмежено віддаляються як від осі  , так і від осі
, так і від осі  .
.
Вісь  називається віссю симетрії параболи. Точка
називається віссю симетрії параболи. Точка 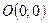 перетину параболи з віссю симетрії називається вершиною параболи. Відрізок
перетину параболи з віссю симетрії називається вершиною параболи. Відрізок 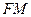 називається фокальним радіусом точки
називається фокальним радіусом точки 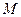 .
.
Для складання рівняння параболи 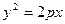 спеціальним чином обрали прямокутну систему координат. Якщо систему координат обрати по-іншому, то рівняння буде мати інший вигляд.
спеціальним чином обрали прямокутну систему координат. Якщо систему координат обрати по-іншому, то рівняння буде мати інший вигляд.
1) 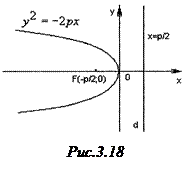 Якщо вісь
Якщо вісь  спрямувати від фокуса до директриси (рис.3.18), то рівняння буде
спрямувати від фокуса до директриси (рис.3.18), то рівняння буде 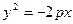 (4).
(4).
Фокус має координати 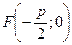 , а директриса
, а директриса 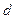 задана рівнянням
задана рівнянням 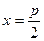 .
.
2) 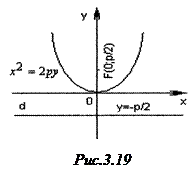 Якщо вісь
Якщо вісь  провести через фокус
провести через фокус 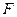 перпендикулярно до директриси
перпендикулярно до директриси 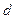 у напрямі від
у напрямі від 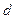 до
до 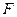 , а початок координат
, а початок координат 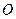 розташувати посередині між фокусом і директрисою (рис.3.19), то рівняння буде
розташувати посередині між фокусом і директрисою (рис.3.19), то рівняння буде 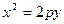 (5).
(5).
Фокус має координати 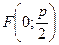 , директриса
, директриса 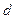 задана рівнянням
задана рівнянням 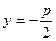 .
.
3) 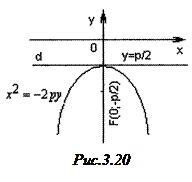 Якщо вісь
Якщо вісь  провести через фокус
провести через фокус 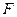 перпендикулярно до директриси
перпендикулярно до директриси 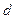 у напрямі від
у напрямі від 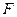 до
до 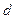 (рис.3.20), то рівняння буде
(рис.3.20), то рівняння буде 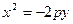 (6).
(6).
Координати її фокуса – 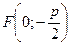 , а рівняння директриси
, а рівняння директриси 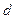 буде
буде 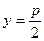 .
.
Про рівняння (4), (5) і (6) кажуть, що вони мають найпростіший вигляд.
Прийнято вважати ексцентриситет параболи рівним одиниці.
Приклад. Дана парабола 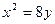 . Знайти координати її фокуса і скласти рівняння директриси.
. Знайти координати її фокуса і скласти рівняння директриси.
Розв’язання. Дана парабола симетрична відносно осі  , вітки напрямлені вгору. Порівнюючи дане рівняння з рівнянням (5), знаходимо
, вітки напрямлені вгору. Порівнюючи дане рівняння з рівнянням (5), знаходимо 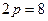 , тобто
, тобто  .
.
Отже, фокус має координати 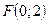 , а рівняння директриси буде
, а рівняння директриси буде 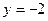 .
.
Відповідь: 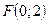 ,
, 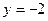 .
.
3. Паралельне перенесення параболи. Нехай дана парабола з вершиною в точці 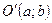 , вісь симетрії якої паралельна осі
, вісь симетрії якої паралельна осі  , а вітки напрямлені вгору (рис.3.21). Тоді її рівняння буде мати вигляд:
, а вітки напрямлені вгору (рис.3.21). Тоді її рівняння буде мати вигляд:
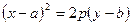 . (7)
. (7)
Рівняння (7) називається рівнянням параболи зі зміщеною вершиною.
Якщо перетворити це рівняння наступним чином:
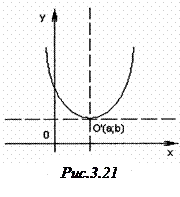
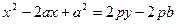 ,
,
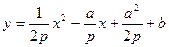 .
.
Поклавши  ,
, 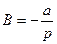 ,
,  , будемо мати
, будемо мати 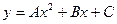 (8), яке знаємо ще зі школи.
(8), яке знаємо ще зі школи.
Приклад. Скласти рівняння параболи з вершиною у точці 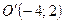 і з фокусом у точці
і з фокусом у точці  .
.
Розв’язання. Вершина і фокус даної параболи лежать на прямій, паралельній осі  (у них однакові абсциси), вітки параболи напрямлені вгору (ордината фокуса більша ординати вершини), відстань від фокуса до вершини дорівнює
(у них однакові абсциси), вітки параболи напрямлені вгору (ордината фокуса більша ординати вершини), відстань від фокуса до вершини дорівнює  , тобто
, тобто 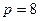 . Підставимо у (7) і отримаємо
. Підставимо у (7) і отримаємо 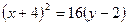 , або
, або  .
.
Відповідь: 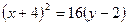 .
.
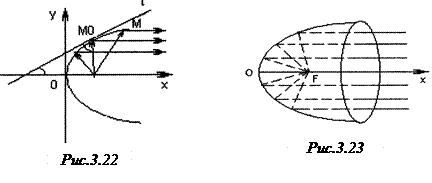 |
4. Застосування параболи до розв’язування прикладних задач. Розглянемо оптичну властивість параболи, яка часто застосовується в техніці (рис.3.22).
Якщо помістити у фокус 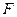 параболи джерело світла (радіохвиль), то промені
параболи джерело світла (радіохвиль), то промені 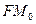 ,
, 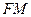 , …, відобразившись від параболи як від дзеркальної поверхні (це означає, що падаючий і відбитий промені утворюють однакові кути з дотичною до параболи в даній точці), будуть напрямлені паралельно осі
, …, відобразившись від параболи як від дзеркальної поверхні (це означає, що падаючий і відбитий промені утворюють однакові кути з дотичною до параболи в даній точці), будуть напрямлені паралельно осі  параболи.
параболи.
Ця властивість використовується для отримання потужного потоку світла (радіохвиль) при обладнанні прожекторів (антен), ряду оптичних приладів.
Приклад. З фокуса параболічного прожектора напрямлено промінь світла у точку 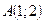 прожектора. Знайти рівняння відбитого променя, якщо осьовий переріз прожектора – парабола
прожектора. Знайти рівняння відбитого променя, якщо осьовий переріз прожектора – парабола 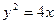 .
.
Розв’язання. У відповідності з оптичною властивістю параболи відображений промінь буде напрямлений паралельно фокальній осі параболи, тобто осі  . Пряма, що містить цей промінь, проходить через точку
. Пряма, що містить цей промінь, проходить через точку 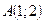 , а отже, має рівняння
, а отже, має рівняння 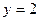 .
.
Відповідь: 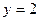 .
.
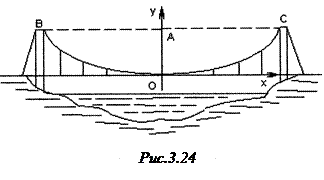 Приклад. Канат підвісного мосту має форму параболи. Потрібно скласти її рівняння відносно вказаних на рис.3.24 осей координат, якщо прогин канату
Приклад. Канат підвісного мосту має форму параболи. Потрібно скласти її рівняння відносно вказаних на рис.3.24 осей координат, якщо прогин канату 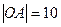 , а довжина мосту
, а довжина мосту  .
.
Розв’язання. Парабола симетрична відносно осі  , вітки напрямлені вгору. Тоді загальний вигляд шуканого рівняння буде
, вітки напрямлені вгору. Тоді загальний вигляд шуканого рівняння буде 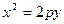 .
.
За умовою точка 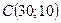 . Ця точка належить параболі, отже,
. Ця точка належить параболі, отже, 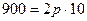 , звідки
, звідки 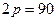 .
.
Шукане рівняння має вигляд 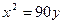 .
.
Відповідь: 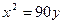 .
.
Приклад. Струмінь води, що її викидає пожежний насос, описує параболічну траекторію з параметром  . Визначити висоту струменя, якщо він падає на відстані
. Визначити висоту струменя, якщо він падає на відстані 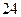 м від місця виходу.
м від місця виходу.
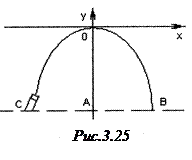 Розв’язання. Розташуємо прямокутну систему координат так: Вісь
Розв’язання. Розташуємо прямокутну систему координат так: Вісь  проходе через найвищу точку струменя води паралельно поверхні землі; вісь
проходе через найвищу точку струменя води паралельно поверхні землі; вісь  також проходе через найвищу точку струменя води (рис.3.25).
також проходе через найвищу точку струменя води (рис.3.25).
Отже, парабола симетрична відносно осі  , вітки напрямлені вниз. Тоді загальний вигляд рівняння траекторії падіння води буде
, вітки напрямлені вниз. Тоді загальний вигляд рівняння траекторії падіння води буде 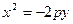 . За умовою
. За умовою  , звідки
, звідки  .
.
За умовою 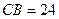 м, тоді
м, тоді 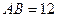 м. Підставимо це у рівняння
м. Підставимо це у рівняння 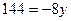 ,
, 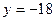 .
.
Отже, 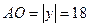 м.
м.
Відповідь:  м.
м.
Контрольні питання
1) Дати означення параболи.
2) Що називається параметром параболи? Як, знаючи параметр параболи, визначити її фокус і директрису?
3) Дати означення осі і вершини параболи. Під яким кутом перетинаються вісь і директриса параболи?
4) Чим відрізняються ексцентриситети еліпса, гіперболи і параболи?
5) В чому полягає оптична властивість параболи?
Читайте також:
- V. Виконання вправ на застосування узагальнювальних правил.
- А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
- Автомобільні ваги із застосуванням цифрових датчиків
- Акти застосування норм права в механізмі правового регулювання.
- Акти застосування юридичних норм: поняття, ознаки, види.
- Акти правозастосування, їх види
- Акти правозастосування.
- Алгоритм із застосування річної процентної ставки r.
- Алгоритм із застосуванням річної облікової ставки d.
- Аміноглікозиди (стрептоміцину сульфат, гентаміцину сульфат). Механізм і спектр протимікробної дії, застосування, побічні ефекти.
- Аналіз зображувальних засобів. Застосування цілісного аналізу
- Антисептики ароматичного ряду (фенол чистий, іхтіол, дьоготь, мазь Вількінсона, лінімент за Вишневським). Особливості протимікробної дії та застосування.
Переглядів: 12262
| <== попередня сторінка | | | наступна сторінка ==> |
| Відповіді | | | Практичне завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |