
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Практичне завдання
3.79. Перевірити, чи лежить: 1) точка 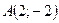 на параболі
на параболі 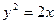 ; 2) точка
; 2) точка 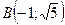 на параболі
на параболі 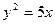 .
.
3.80. Скласти рівняння чотирьох парабол з вершиною в початку координат, знаючи, що координати їх фокусів дорівнюють: 1) 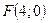 ; 2)
; 2) 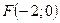 ; 3)
; 3)  ; 4)
; 4) 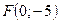 .
.
3.81. Визначити координати фокусів таких парабол: 1) 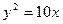 ; 2)
; 2) 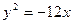 ; 3)
; 3) 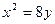 ; 4)
; 4) 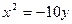 .
.
3.82. Знайти координати фокуса параболи 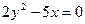 .
.
3.83. Скласти рівняння парабол, знаючи координати вершини 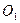 і фокуса
і фокуса 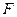 : 1)
: 1) 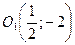 ,
,  ; 2)
; 2) 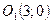 ,
, 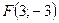 .
.
3.84. Скласти рівняння парабол з вершиною в початку координат, для яких директрисами є прямі: 1) 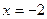 ; 2)
; 2) 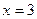 ; 3)
; 3) 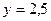 ; 4)
; 4) 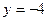 .
.
3.85. Записати рівняння директриси і знайти координати фокуса кожної з парабол: 1) 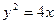 ; 2)
; 2)  .
.
3.86. Директрисою параболи з вершиною в початку координат є пряма 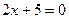 . Скласти рівняння і визначити координати фокуса цієї параболи.
. Скласти рівняння і визначити координати фокуса цієї параболи.
3.87. Фокус параболи має координати 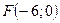 , а рівняння директриси
, а рівняння директриси 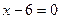 . Скласти рівняння параболи.
. Скласти рівняння параболи.
3.88. Скласти рівняння параболи, якщо координати фокуса 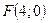 , а рівняння директриси
, а рівняння директриси 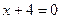 .
.
3.89. Побудувати параболу  . Знайти: 1) координати фокуса; 2) рівняння директриси.
. Знайти: 1) координати фокуса; 2) рівняння директриси.
3.90. Скласти канонічне рівняння параболи, яка має вершину в початку координат, симетрична відносно осі  і проходить через точку
і проходить через точку 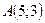 .
.
3.91. Скласти рівняння параболи, яка має вершину в початку координат, симетрична відносно осі  і проходить через точку
і проходить через точку 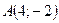 .
.
3.92. Скласти рівняння параболи, яка має вершину в початку координат, симетрична відносно осі  і проходить через точку
і проходить через точку 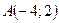 .
.
3.93. Скласти рівняння параболи, що проходить через початок координат і симетрична відносно осі ординат, якщо координати фокуса 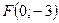 .
.
3.94. Скласти рівняння параболи: 1) що проходить через точки 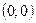 і
і  та симетрична відносно осі
та симетрична відносно осі  ; 2) що проходить через точки
; 2) що проходить через точки 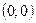 і
і 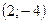 та симетрична відносно осі
та симетрична відносно осі  .
.
3.95. Знайти координати вершини, величину параметра і напрям парабол: 1) 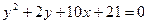 ; 2)
; 2) 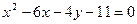 .
.
3.96. Знайти точки перетину параболи 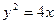 : 1) з прямою
: 1) з прямою 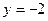 ; 2) з прямою
; 2) з прямою 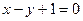 ; 3) з прямою
; 3) з прямою 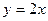 ; 4) з гіперболою
; 4) з гіперболою 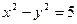 .
.
3.97. Знайти точки перетину параболи 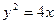 і прямих: 1)
і прямих: 1) 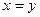 ; 2)
; 2) 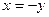 ; 3)
; 3) 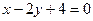 ; 4)
; 4) 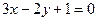 . Побудувати креслення.
. Побудувати креслення.
3.98. Знайти точки перетину параболи 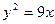 з прямими: 1)
з прямими: 1) 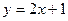 ; 2)
; 2)  ; 3)
; 3)  .
.
3.99. Парабола проходить через точки 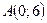 і
і 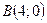 симетрично відносно осі абсцис. Скласти рівняння параболи і побудувати.
симетрично відносно осі абсцис. Скласти рівняння параболи і побудувати.
3.100. Дано фокус параболи 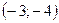 і рівняння її директриси
і рівняння її директриси 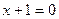 . Скласти рівняння параболи і знайти точки перетину параболи з осями координат.
. Скласти рівняння параболи і знайти точки перетину параболи з осями координат.
3.101. Через фокус параболи 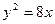 і через її точку, абсциса якої дорівнює
і через її точку, абсциса якої дорівнює 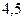 , а ордината додатна, проведено січну. Скласти рівняння січної.
, а ордината додатна, проведено січну. Скласти рівняння січної.
3.102. Знайти координати вершини і фокуса, а також рівняння осі симетрії і директриси параболи: 1) 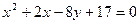 ; 2)
; 2) 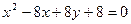 ; 3)
; 3) 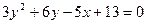 ; 4)
; 4) 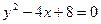 ; 5)
; 5) 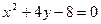 .
.
3.103. Знайти рівняння параболи, знаючи, що її вершина знаходиться в точці 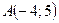 , а фокус в точці
, а фокус в точці  . Записати рівняння її осі і директриси.
. Записати рівняння її осі і директриси.
3.104. Знайти на параболі 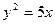 точки, у яких абсциси і ординати однакові.
точки, у яких абсциси і ординати однакові.
3.105. Камінь, кинутий з даху будинку паралельно горизонту, падає на землю, описуючи параболу 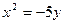 . На якій відстані від вертикалі впаде камінь на землю, якщо висота будинку 20м?
. На якій відстані від вертикалі впаде камінь на землю, якщо висота будинку 20м?
3.106. Камінь, кинутий під гострим кутом до горизонту, описує дугу параболи і падає на відстані 16м від початкового положення. Записати найпростіше рівняння параболи, коли відомо, що найбільша висота підйому каменя 12м.
3.107. Перерізом рефлектора площиною, що проходить через вісь рефлектора є парабола. Записати її рівняння, якщо ширина рефлектора 30см, а глибина 20см (вісь рефлектора збігається з віссю  ).
).
3.108. Знайти висоту арки мосту завдовжки 24м, якщо арка має форму параболи, рівняння якої 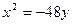 .
.
3.109. Параболічне дзеркало рефлектора Симеїзької обсерваторії має діаметр 1,02м; відстань його фокуса від вершини дорівнює 5м. Знайти глибину параболічної виїмки, яку довелося зробити під час виготовлення дзеркала з плоского скла.
3.110. З отвору бака, який знаходиться на поверхні землі, витікає вода струменем, що представляє собою дугу параболи 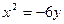 , якщо за початок координат прийняти отвір бака, а вісь
, якщо за початок координат прийняти отвір бака, а вісь  спрямувати вертикально вгору. На якій відстані від краю бака падає струмінь на землю, якщо висота отвору 1,5м?
спрямувати вертикально вгору. На якій відстані від краю бака падає струмінь на землю, якщо висота отвору 1,5м?
Читайте також:
- V. ДОМАШНЄ ЗАВДАННЯ
- V. ДОМАШНЄ ЗАВДАННЯ
- V. Завдання.
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
- Vi. домашнє завдання
- Vi. домашнє завдання
- VI. ДОМАШНЄ ЗАВДАННЯ
- VI. ДОМАШНЄ ЗАВДАННЯ
| <== попередня сторінка | | | наступна сторінка ==> |
| Парабола та її застосування | | | Відповіді |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |