
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Графічний метод розв'язування задач НП
Як було зазначено вище, для ЗНП не існує єдиного методу їх розв'язування. Коли число змінних задачі 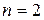 , то скористаємося графічним методом, алгоритм якого наступний:
, то скористаємося графічним методом, алгоритм якого наступний:
1) будуємо область допустимих розв’язків задачі і лінії рівня для цільової функції.
2) в точці або сукупності точок, де лінія рівня перший раз торкнеться області допустимих розв'язків, цільова функція буде набувати мінiмального значення. Підставивши координати точок дотику в цільову функцію, знайдемо величину мінімуму.
3) підставивши в цільову функцію координати тих точок, в яких лінія рівня останній раз торкнеться області допустимих розв'язків, отримаємо величину глобального максимуму.
Приклад 4.6. Знайти найменше значення функції  при обмеженнях
при обмеженнях

Розв'язок. Область допустимих розв'язків представляє собою многокутник АВСЕ (рис. 4.1). Побудуємо лінії рівня цільової функції, поклавши  . Отримаємо рівняння кола
. Отримаємо рівняння кола  . Збільшуючи чи зменшуючи значення с( квадрат радіуса), ми будемо збільшувати чи зменшувати значення цільової функції, тобто лінії рівня є колами з центром у точці М(4; 6) та радіусами
. Збільшуючи чи зменшуючи значення с( квадрат радіуса), ми будемо збільшувати чи зменшувати значення цільової функції, тобто лінії рівня є колами з центром у точці М(4; 6) та радіусами  . Провівши з точки M, концентричні кола різних радіусів, одержимо, що мінімальне значення функція f набуваєв точці D, в якій коло дотикається до області розв’язків. Точка D не є кутовою, її координати знайдемо, розв’язавши систему рівнянь
. Провівши з точки M, концентричні кола різних радіусів, одержимо, що мінімальне значення функція f набуваєв точці D, в якій коло дотикається до області розв’язків. Точка D не є кутовою, її координати знайдемо, розв’язавши систему рівнянь

Тут 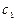 є тим значенням, при якому коло дотикається області розв’язків у точці D. З другого рівняння системи
є тим значенням, при якому коло дотикається області розв’язків у точці D. З другого рівняння системи
 .
.
Підставивши його в перше рівняння, отримаємо:
 .
.
Звідси, шляхом нескладних перетворень приходимо до квадратного рівняння відносно  :
:
 .
.
Оскільки D – це точка дотику кола і прямої, то отримане рівняння повинно мати єдиний розв’язок, а це можливо тоді, коли дискримінант дорівнює нулю.
Маємо рівняння
 .
.
Звідси знаходимо 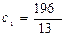 функція набуває в точці
функція набуває в точці  .
.
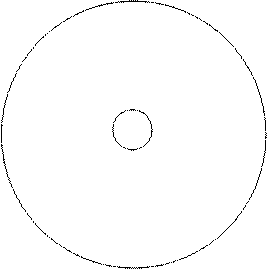 |

Рис. 4.1.
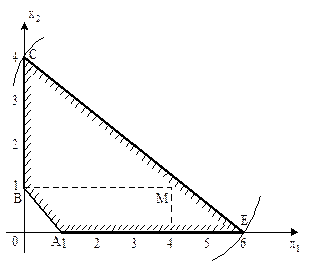
Рис. 4.2.
Розв'язок перевіримо методом множників Лагранжа. Врахувавши, що найменше значення досягається на прямій 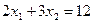 , отримаємо нову задачу: знайти найменше значення функцїї
, отримаємо нову задачу: знайти найменше значення функцїї  при умові
при умові 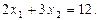 Будуємо функцію Лагранжа (4.7) .
Будуємо функцію Лагранжа (4.7) .
 .
.
Тоді система рівнянь (4.10) має вигляд
 або
або 
а її розв'язок 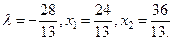 Точка D з координатами
Точка D з координатами  – стаціонарна точка. ЇЇ координати співпадають з одержаними раніше графічним методом. Знаходимо другі частинні похідні функції L і обчислимо їх значення у критичній точці.
– стаціонарна точка. ЇЇ координати співпадають з одержаними раніше графічним методом. Знаходимо другі частинні похідні функції L і обчислимо їх значення у критичній точці.
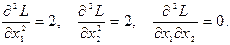
Запишемо  . З обмеження
. З обмеження  знаходимо зв’язки на диференціали
знаходимо зв’язки на диференціали 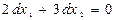 ,
,  . Тоді
. Тоді
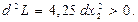
Оскільки 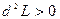 , то D – точка мінімуму.
, то D – точка мінімуму.
Приклад 4.7. За умовою прикладу 4.6 знайти найменше і найбільше значення функції  .
.
Розв’язок. Найменше значення функція приймає в точці М(4;1) (рис.4.2): f (M)=0.Функція z має два локальних максимуми: в вершині Е(6;0) функція f (E)=5, в вершині С(0;4) функція f (C)=25, причому глобальний максимум досягається в вершині С і 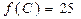 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Метод множників Лагранжа. Економічний зміст множників Лагранжа | | | Теорема Куна-Таккера |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |