• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Метод множників Лагранжа. Економічний зміст множників Лагранжа

Розглянемо наступну ЗНП: знайти найбільше значення цільової функції

(4.20)

при обмеженнях

, (4.21)

Оскільки обмеження задачі задані рівняннями, то для знаходження розв’язку задачі можна скористатися класичним методом знаходження умовного екстремуму для функцій багатьох змінних. При цьому будемо припускати, що функції 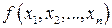, , неперервні разом зі своїми першими частинними похідними. Для знаходження розв'язку задачі складемо функцію Лагранжа (4.7).

Знайшовши частинні похідні і 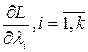, за виконання умов (4.8) і (4.9) систему (4.10) запишемо у вигляді

(4.22)

яка задає необхідні умови того, щоб функція (4.20) в точці досягала локального умовного екстремуму.

Якщо для функцій 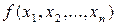і 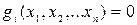існують частинні похідні другого порядку і є неперервними та виконуються достатні умови існування локального екстремуму функції в точці , координати якої є розв'язком системи (4.22), а саме, якщо другий диференціал функції в точці є додатно (від’ємно) визначена квадратична форма, то є точкою локального мінімуму (максимуму), якщо ж квадратична форма невизначена, то в точці 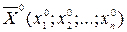екстремуму не існує.

Наведемо алгоритм розв'язування задачі (4.20) — (4.21) методом множників Лагранжа:

1) записати функцію Лагранжа (4.7);

2) знайти частинні похідні і , і розв'язавши отриману систему (4.22), знайти всі стаціонарні точки функції Лагранжа;

3) із стаціонарних точок, взятих без множників вибрати ті, в яких функція Лагранжа (4.7) досягає умовного локального екстремуму.

Дамо тепер економічну інтерпретацію множників Лагранжа. Для цього розглянемо задачу: знайти найбільше значення функції при обмеженнях .

Припустимо, що умовний екстремум досягається в точці 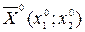і рівний 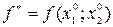, а величина в обмеженні може змінюватися. Тоді координати точки екстремуму і екстремальне значення 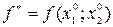стануть залежними від : тобто

. (4.23)

Оскільки , то

(4.24)

Крім того, в точці екстремуму 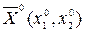, виконуються необхідні умови (4.22).Звідки для 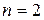і отримаємо

(4.25)

Підставляючи (4.25) в (4.23) і враховуючи (4.24), отримаємо:

Аналогічно для задачі (4.20)–(4.21) одержимо

Якщо 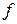інтерпретувати як дохід або вартість, а 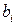– як об'єми деяких ресурсів, то множники Лагранжа , показують, як зміниться максимальний дохід (або мінімальна вартість), якщо кількість ресурсу –го виду збільшиться на одиницю.

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
5. I. Метод рiвних вiдрiзкiв.
6. VII. Нахождение общего решения методом характеристик
7. А. науковий факт, b. гіпотеза, с. метод
8. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
9. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
10. Агресивний тип дивідендної політики включає метод стабільного приросту дивідендів і метод постійного коефіцієнта виплат.
11. АгротехнІЧНИЙ метод
12. Адаптовані й специфічні методи дослідження у журналістикознавстві

Переглядів: 2274