• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Електроенергетика

На основі ШНМ ГП з додатковими латеральними зв’язками між нейронами прихованого шару за допомогою методу “часових вікон” було здійснене прогнозування споживання електричної енергії у Львівській області на основі даних знятих засобами телеметрії у ЕПК ВАТ “Львівобленерго”. Вхідні статистичні дані попередньо доповнювалися і апроксимувалися за допомогою методу найменших квадратів.

На етапі навчаня ШНМ входами навчальної вибірки приймають векторну множину , до якої входять: - місяць, - декада, 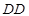- день в декаді, 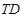- тип дня в декаді, 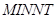- мінімальна нічна температура повітря, - максимальна нічна температура повітря, - мінімальна денна температура повітря, 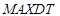- максимальна денна температура повітря, - мінімальна швидкість вітру, 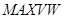- максимальна швидкість вітру, 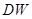- напрямок вітру, 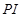- погодинні значення потужностей навантаження. Виходами ШНМ (векторна множина ) є - погодинні зпрогнозовані значення потужностей навантаження.

Тобто навчання здійснюється за схемою:

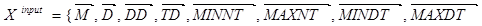
Реалізація моделі здійснюється шляхом заміни навчальних входів на реальні дані телеметрії 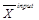, якими є значення телевимірів (ТВ), що надходять на концентратор інформації оперативного інформаційно-керуючого комплексу ВАТ “Львівобленерго”. Тоді виходами будуть погодинні зпрогнозовані значення потужностей навантаження.

Вхідні дані кодуються наступним чином: Місяць – 1, 2, ..., 11,12; Декада – 1,2,3; День в декаді – 1, 2,..., 10, 11; Тип дня – (+1 – будній день, -1 –вихідний або святковий день ); Температура повітря – (-30,...,+40); Швидкість вітру – (1,...,16); Напрямок вітру згідно схеми зображеної на Рис. 20.7.

Рис. 20.7. Кодування напрямків вітру.

ШНМ навчалася на основі даних ТМ за період 1999-2000 роки з середньоквадратичною зведеною похибкою відтворення 3,4%, максимальною зведеною похибкою11,2%.

При тестуванні ШНМ на реальних даних, що були отримані за період 2001-2002 років з середньоквадратичною зведеною похибкою 5,4%, та максимальною зведеною похибкою 15,9% (див. Рис. 20.8. навчання 240 год, далі прогноз), що цілком задовільняє вимогам практики.

Рис. 20.8. Результати прогнозування споживання електричної енергії Львівською областю за допомогою ФМТФ ШНМ на: а) добу; б) дві доби; в) п’ять діб; г) тиждень. (1-прогноз, 2-реальні дані).

Контрольні запитання

1. Приклади застосування ШНМ у сфері фінансів.

2. Інформативні параметри при прогнозуванні економічних показників.

3. Можлива точність прогнозів при прогнозуванні у фінансовій сфері.

4. Особливості прогнозування фізичних процесів.

5. Точність прогнозування показників енергоспоживання.

Лекція № 21.Застосування засобів ШІ для опрацювання зображень.

Розпізнавання цифр

Серед різних конфігурацій нейронних мереж для розпізнавання образів зустрічаються такі, для яких не підходять ні навчання з вчителем, ні навчання без вчителя. У таких мережах вагові коефіцієнти обчислюються тільки один раз перед початком функціонування мережі на основі інформації про оброблювані дані. Такі мережі одержали назву статичних. З подібних мереж найбільш відомі мережа Гопфілда і мережа Гемінга, що звичайно використовуються для організації асоціативної пам'яті. Нижче показано мережу Гемінга (Рис. 21.1). Вона характеризується, у порівнянні з мережею Гопфілда, меншими витратами на пам'ять і обсяг обчислень.

Ця мережа складається з двох шарів. Кожен шар має по m нейронів , де m - число образів. Нейрони першого шару мають по n синапсів, з'єднаних із входами мережі. Нейрони другого шару зв'язані між собою негативними зворотніми (інгібіторними) зв'язками. Єдиний синапс із позитивним зворотнім зв'язком, який утворює торсійне поле для кожного нейрона з'єднаний з його ж аксоном.

Ідея роботи мережі полягає в оцінці величини зворотньої відстані Гемінга від образу що тестується до всіх еталонних зразків (відстанню Гемінга називається число що відрізняється бітом у двох бінарних векторах). Мережа повинна вибрати зразок з мінімальною відстанню Гемінга до невідомого вхідного сигналу - і буде активізований тільки один вихід мережі, що відповідає цьому зразку.

Рис. 21.1.Структура мережі Гемінга.

Активаційна функція нейронів першого і другого шару має вигляд лінійного порога:

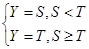
де:
Y - значення активационой функції;
S - аргумент активационой функції;
T - величина порога.
Величина T повинна бути досить великою, щоб будь-які можливі значення аргументу не приводили до насичення.

Ініціалізація і загальний алгоритм функціонування

На стадії ініціалізації ваговим коефіцієнтам першого шару присвоюються наступні значення:

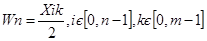
де:
X_ik - i-й елемент k-го зразка.

X_ik приймає значення -1 для одного типу вхідних крапок і 1 для іншого типу. Порогові активаційної функції першого шару T присвоюється значення n/2.

Вагові коефіцієнти гальмуючих синапсів у другому шарі беруть рівними деякій величині 0 < e < 1/m , взятих зі зворотнім знаком. Синапс нейрона,

зв'язаний з його ж аксоном має вагу +1 (див. Рис. 21.1).

Алгоритм функціонування мережі Гемінга наступний:

На входи мережі подається невідомий вектор X, виходячи з якого розраховуються стани нейронів першого шару, що передаються на вхід другого шару.

Обчислюються стани нейронів другого шару.

Перевіряється, чи змінилися виходи нейронів другого шару за останню ітерацію. Якщо так - перейди до кроку 2. Інакше - виходи стабілізувалися і робота мережі завершена.

Результат роботи даної мережі продемонстрований для розпізнавання рукописних і друкованих цифр від 0 до 9. На прикладі Рис.21.2 розпізнається п’ятірка .

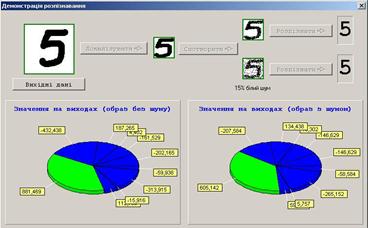
Рис.21.2. Приклад розпізнавання цифр.

Аналогічним чином здійснюється розпізнавання тексту, опрацьовуючи його ще додатковими словниками і більш складних образів з багатокольоровими гама­ми.

Розпізнавання друкованого тексту

Перцептрон навчають, подаючи множину образів по одному на його вхід і налаштовуючи ваги доти, поки для всіх образів не буде досягнуть необхідний вихід. Допустимо, що вхідні образи нанесені на демонстраційні карти. Кожна карта розбита на квадрати і від кожного квадрата на перцептрон подається вхід. Якщо в квадраті є лінія, то від нього подається одиниця, в іншому випадку - нуль. Множина квадратів на карті задає, таким чином, множину нулів і одиниць, яка і подається на входи перцептрону. Мета полягає в тому, щоб навчити перцептрон включати індикатор при подачі на нього множини входів, що задають непарне число, і не включати у разі парного.

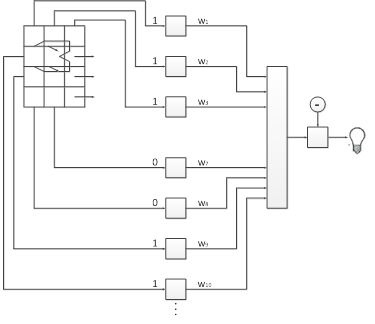
Рис. 21.3. Перцептронна система розпізнавання зображень

На рис. 21.3 показана перцептронная конфігурація. Припустимо, що вектор Х є образом розпізнаваної демонстраційної карти. Кожна компонента (квадрат) Х - (x1, x2, ..., xn) множиться на відповідну компоненту вектора ваг W - (w1, w2,..., wn). Ці добутки підсумовуються. Якщо сума перевищує поріг Θ, тоді вихід нейрона Y рівний одиниці (індикатор запалюється), в іншому випадку він - нуль. Як ми бачили в розділі 1, ця операція компактно записується у векторній формі як Y = XW, а після неї слідує порогова операція.

Для навчання мережі зразок Х подається на вхід і обчислюється вихід Y. Якщо Y правильний, то нічого не міняється. Однак якщо вихід неправильний, то ваги, приєднані до входів, що підсилюють помилковий результат, модифікуються, щоб зменшити похибку.

Щоб побачити, як це здійснюється, припустимо, що демонстраційна карта з цифрою 3 подана на вхід і вихід Y рівний 1 (показуючи непарність). Оскільки це правильна відповідь, то ваги не змінюються. Якщо, однак, на вхід подається карта з номером 4 і вихід Y рівний одиниці (непарний), то ваги, приєднані до одиничних входів, повинні бути зменшені, оскільки вони прагнуть дати невірний результат. Аналогічно, якщо карта з номером 3 дає нульовий вихід, то ваги, приєднані до одиничних входів, повинні бути збільшені, щоб скоректувати похибку.

Цей метод навчання може бути підсумований таким чином:

1. Подати вхідний зразок і обчислити Y.

2. Якщо вихід правильний, то перейти на крок 1;

· Якщо вихід неправильний і рівний нулю, то додати всі входи до відповідної ним ваги;або

· Якщо вихід неправильний і рівний одиниці, то відняти кожний вхід з відповідної йому ваги.

· Перейти на крок 1.

За кінцеве число кроків мережа навчиться розділяти карти на парні і непарні при умові, що множина цифр лінійно роздільна. Це означає, що для всіх непарних карт вихід буде більшим за поріг, а для всіх парних менше. Зазначимо, що це навчання глобальне, тобто мережа навчається на всій множині карт.

Переглядів: 1169