
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Повернення до кроку 2.
Рис. 14.1. Мережа Когонена
Топологічно мережа Когонена (рис. 14.1) має всього два прошарки: вхідний і вихідний, що називають самоорганізованою картою. Елементи карти розташовуються в деякому просторі - як правило двовимірному. Мережа Когонена навчається методом послідовних наближень. Починаючи з випадковим чином обраного вихідного розташування центрів, алгоритм поступово покращується для кластеризації навчальних даних. Проте, алгоритм може працювати і на іншому рівні. В результаті ітеративної процедури навчання мережа організовується таким чином, що елементи, які відповідають центрам, розташованим близько один від одного в просторі входів, будуть розташовані близько один від одного і на топологічній карті. Топологічний прошарок мережі можна уявити як двовимірну штахету, яку потрібно так відобразити в N-вимірний простір входів, щоб по можливості зберегти вихідну структуру даних. Звісно ж, при будь-якій спробі відтворити N-вимірний простір на площині буде загублено багато деталей, але такий прийом дозволяє користувачу візуалізувати дані, що неможливо зрозуміти іншим засобом. Основний ітераційний алгоритм Когонена послідовно проходить ряд епох, на кожній епосі опрацьовується один навчальний приклад. Вхідні сигнали - вектори дійсних чисел - послідовно пред'являються мережі. Бажані вихідні сигнали не визначаються. Після пред'явлення достатньої кількості вхідних векторів, синаптичні ваги мережі визначають кластери. Крім того, ваги організуються так, що топологічно близькі вузли чутливі до схожих вхідних сигналів.
Для реалізації алгоритму необхідно визначити міру сусідства нейронів (окіл нейрона-переможця). На рис. 14.2 показані зони топологічного сусідства нейронів на карті ознак у різні моменти часу. NEj(t) - множина нейронів, що вважаються сусідами нейрона j у момент часу t. Зони сусідства зменшуються з часом.
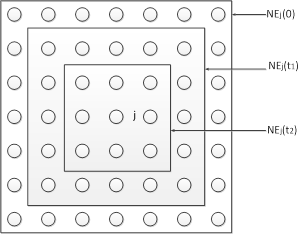
Рис. 14.2. Зони топологічного сусідства на карті ознак у різні моменти часу
Алгоритм функціонування мережі Когонена:
1. Ініціалізація мережі. Ваговим коефіцієнтам мережі надаються малі випадкові значення. Початкова зона сусідства показана на рис. 14.2.
2. Пред'явлення мережі нового вхідного сигналу.
3. Обчислення відстані до всіх нейронів мережі:
Відстані dj від вхідного сигналу до кожного нейрона j визначаються за формулою:

де xi - i-ий елемент вхідного сигналу в момент часу t, wij(t) - вага зв'язку від i-го елемента вхідного сигналу до нейрона j у момент часу t.
4. Вибір нейрона з найменшою відстанню:
Вибирається нейрон-переможець j*, для якого відстань dj найменша.
5. Налаштування ваг нейрона j* і його сусідів:
Робиться налаштування ваг для нейрона j* і всіх нейронів з його околу NE. Нові значення ваг:
wij(t+1)=wij(t)+r(t)(xi(t)-wij(t))
де r(t) - швидкість навчання, що зменшується з часом (додатнє число, менше одиниці).
В алгоритмі використовується коефіцієнт швидкості навчання, який поступово зменшується, для точнішої корекції на новій епосі. В результаті позиція центру встановлюється в певній позиції, що задовільним чином кластеризує приклади, для яких даний нейрон є переможцем.
Властивість топологічної впорядкованості досягається в алгоритмі за допомогою використання поняття околу. Окіл - це декілька нейронів, що оточують нейрон-переможець. Відповідно до швидкості навчання, розмір околу поступово зменшується, так, що спочатку до нього належить досить велика кількість нейронів (можливо вся карта), на самих останніх етапах окіл стає нульовим і складається лише з нейрона-переможця. В алгоритмі навчання корекція застосовується не тільки до нейрона-переможця, але і до всіх нейронів з його поточного околу. В результаті такої зміни околу, початкові доволі великі ділянки мережі мігрують в бік навчальних прикладів. Мережа формує грубу структуру топологічного порядку, при якій схожі приклади активують групи нейронів, що близько знаходяться на топологічній карті. З кожною новою епохою швидкість навчання і розмір околу зменшуються, тим самим всередині ділянок карти виявляються більш тонкі розходження, що зрештою призводить до точнішого налаштування кожного нейрона. Часто навчання зумисне розбивають на дві фази: більш коротку, з великою швидкістю навчання і великих околів, і більш тривалу з малою швидкістю навчання і нульовими або майже нульовими околами.
Після того, як мережа навчена розпізнаванню структури даних, її можна використовувати як засіб візуалізації при аналізі даних.
Області застосуванн:. Кластерний аналіз, розпізнавання образів, класифікація. Недоліки: мережа може бути використана для кластерного аналізу тільки в тому випадку, якщо заздалегідь відоме число кластерів. Переваги: мережа Когонена здатна функціонувати в умовах перешкод, тому що число кластерів фіксоване, ваги модифікуються повільно, налаштування ваг закінчується після навчання. Модифікації: одна з модифікацій полягає в тому, що до мережі Когонена додається мережа MAXNET, що визначає нейрон з найменшою відстанню до вхідного сигналу.
Нейромережі комбінованого типу. Використовують в своїй основі каскадний принцип побудови. Прикладом таких ШНМ є мережа зустрічного поширення.
Роберт Гехт-Нільсен (Robert Hecht-Nielsen) розробив мережу зустрічного поширення (СounterРropagation) як засіб для поєднання неконтрольованого прошарку Когонена із контрольованим вихідним прошарком. Мережа призначена для вирішення складних задач класифікації, за умови мінімізації числа нейронів та часу навчання. Навчання для мережі СounterРropagation подібне до мережі з квантуванням навчального вектора.
Приклад мережі зображений на рис. 14.6. Односкерована мережа CounterPropagation має три прошарки: вхідний прошарок, самоорганізовану карту Когонена та вихідний прошарок, що використовує правило "дельта" для зміни вхідних ваг з'єднань. Цей прошарок називають прошарком Гросберга.

Рис. 14.6. Мережа зустрічного поширення без зворотних зв'язків
Перша мережа СounterРropagation складалась із двоскерованого відображення між вхідним та вихідним прошарками. Дані надходять на вхідний прошарок для генерації класифікації на вихідному прошарку, вихідний прошарок по черзі приймає додатковий вхідний вектор та генерує вихідну класифікацію на вхідному прошарку мережі. Через такий зустрічно-поширений потік інформації випливає назва мережі. Багато розробників використовують односкерований варіант СounterРropagation, коли існує лише один шлях прямого поширення від вхідного до вихідного прошарку.
У мережі зустрічного поширення об'єднані два алгоритми: самоорганізована карта Когонена і зірка Гросберга (Grossberg Outstar). Кожен елемент вхідного сигналу подається на всі нейрони прошарку Когонена. Ваги зв'язків (wmn) утворюють матрицю W. Кожен нейрон прошарку Когонена з'єднаний зі всіма нейронами прошарку Гросберга. Ваги зв'язків (vnp) утворюють матрицю ваг V. Нейронні мережі, що поєднують різні нейропарадигми як будівельні блоки, більш близькі до мозку по архітектурі, ніж однорідні структури. Вважається, що в мозку саме каскадні з'єднання модулів різної спеціалізації дозволяють виконувати необхідні обчислення.
У процесі навчання мережі зустрічного поширення вхідні вектори асоціюються з відповідними вихідними векторами (двійковими або аналоговими). Після навчання мережа формує вихідні сигнали, що відповідають вхідним сигналам. Узагальнююча здатність мережі дає можливість одержувати правильний вихід, якщо вхідний вектор неповний чи спотворений.
Навчання мережі
Карта Когонена класифікує вхідні вектори в групи схожих. В результаті самонавчання прошарок здобуває здатність розділяти несхожі вхідні вектори. Який саме нейрон буде активуватися при пред'явленні конкретного вхідного сигналу, заздалегідь важко передбачити.
При навчанні прошарку Когонена на вхід подається вхідний вектор і обчислюються його скалярні добутки з векторами ваг всіх нейронів.
Скалярний добуток є мірою подібності між вхідним вектором і вектором ваг. Нейрон з максимальним значенням скалярного добутку з'являється "переможцем" і його ваги підсилюються (ваговий вектор наближається до вхідного).
wн=wc+r(x-wc)
де wн - нове значення ваги, що з'єднує вхідний компонент x з нейроном-переможцем, wс - попереднє значення цієї ваги, r - коефіцієнт швидкості навчання, що спочатку звичайно дорівнює 0.7 і може поступово зменшуватися в процесі навчання. Це дозволяє робити великі початкові кроки для швидкого грубого навчання і менші кроки при підході до остаточної величини.
Кожна вага, зв'язана з нейроном-переможцем Когонена, змінюється пропорційно різниці між його величиною і величиною входу, до якого він приєднаний. Напрямок зміни мінімізує різницю між вагою і відповідним елементом вхідного прошарку.
Навчальна множина може містити багато подібних між собою вхідних векторів, і мережа повинна бути навченою активувати один нейрон Когонена для кожного з них. Ваги цього нейрона уявляють собою усереднення вхідних векторів, що його активують.
Виходи прошарку Когонена подаються на входи нейронів прошарку Гросберга. Входи нейронів обчислюються як зважена сума виходів прошарку Когонена. Кожна вага коректується лише в тому випадку, якщо вона з'єднана з нейроном Когонена, який має ненульовий вихід. Величина корекції ваги пропорційна різниці між вагою і необхідним виходом нейрона Гросберга. Навчання прошарку Гросберга - це навчання "з вчителем", алгоритм використовує задані бажані виходи.
Функціонування мережі
У своїй найпростішій формі прошарок Когонена функціонує за правилом "переможець отримує все". Для даного вхідного вектора один і тільки один нейрон Когонена видає логічну одиницю, всі інші видають нуль.
Прошарок Гросберга функціонує в схожій манері. Його вихід є зваженою сумою виходів прошарку Когонена.
Якщо прошарок Когонена функціонує таким чином, що лише один вихід дорівнює одиниці, а інші дорівнюють нулю, то кожен нейрон прошарку Гросберга видає величину ваги, що зв'язує цей нейрон з єдиним нейроном Когонена, чий вихід відмінний від нуля.
У повній моделі мережі зустрічного поширення є можливість одержувати вихідні сигнали по вхідним і навпаки. Цим двом діям відповідають пряме і зворотне поширення сигналів.
Області застосування: розпізнавання образів, відновлення образів (асоціативна пам'ять), стиснення даних (із втратами). Недоліки. Мережа не дає можливості будувати точні апроксимації (точні відображення). У цьому мережа значно поступається мережам зі зворотним поширенням похибки. До недоліків моделі також варто віднести слабкий теоретичний базис модифікацій мережі зустрічного поширення. зустрічного поширення.
· Мережа зустрічного поширення достатньо проста. Вона надає можливість отримувати статистичні властивості з множини вхідних сигналів. Когонен довів, що для навченої мережі ймовірність того, що випадково обраний вхідний вектор буде найближчим до будь-якого заданого вагового вектора, дорівнює 1/k, k - число нейронів Когонена.
· Мережа швидко навчається. Час навчання в порівнянні зі зворотним поширенням може бути в 100 разів меншим.
· По своїх можливостях будувати відображення мережа зустрічного поширення значно перевершує одношарові перцептрони.
· Мережа корисна для застосувань, у яких потрібно швидка початкова апроксимація.
Контрольні запитання
1. Який режим навчання застосовується для само організаційних карт Когонена?
2. Області застосування карт Когонена.
3. Основи алгоритму навчання карт Когонена.
4. Топологія карт Когонена.
5. В чому полягають аналогії між картами Когонена і корою головного мозку?
6. Топологія ШНМ зустрічного поширення.
7. Основні властивості ШНМ зустрічного поширення.
Лекція № 15.Одношарові і багатошарові перцептрони в режимі прогнозування часових послідовностей.
Часовою послідовністю є дискретизована залежність, яка описує зміни параметрів процесу в часі. Розглядають одно параметричні і багато параметричні послідовності.
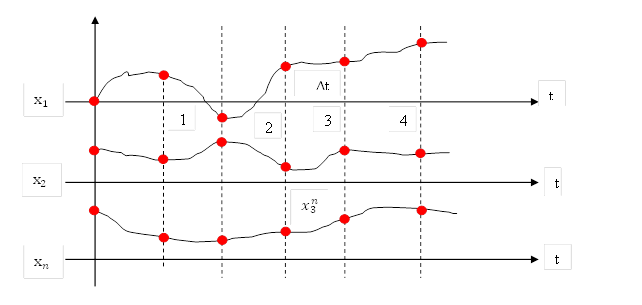
Рис. 15.1. Багатопараметричний процес
На рисунку 15.1 багатопараметричний процес представлений часовими залежностями параметрів х1, х2, …, хn; дискретизація параметрів виконана через однакові проміжки часу Δt; можливий варіант нерівномірної дискретизації, який використовується однак рідко. Параметри х1, х2, …, хn можуть мати різну природу, зокрема частина з них можуть бути незалежними, а частина – взаємозалежними. Деякі з параметрів можуть бути відомими на усьому часовому проміжку, отже вони не підлягають прогнозуванню. Однак основні параметри відомі лише до заданого, фіксованого моменту часу. Метою прогнозування є отримання невідомих раніше прогнозних значень.
Існуючі методи прогнозування оперують дискретизованими значеннями параметрів
 ,
, 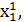
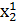 , …
, …
 ,
, 
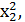 …
…


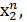 …
…
Верхній індекс – номер параметра, нижній – номер відліку.
Передісторія часової послідовності – це відомі значення відліків, до моменту здійснення прогнозів. Довжина передісторії – число відомих відліків.
Горизонт прогнозування – кількість відліків, для яких необхідно отримати прогнозні значення.
Використовують різноманітні засоби і методи для здійснення прогнозів, але у всіх випадках прогнозоване значення отримують на основі значень передісторії. Виключенням є процеси, які описуються так званими марківськими ланцюгами, для яких значення у наступний момент часу залежить лише від відповідного значення у попередній момент часу.
Як приклад засобів для прогнозування можна назвати передбачаючі фільтри, наприклад фільтр Калмана-Бюсі. Найбільш ефективними і точними методами на даний час вважають нейромережні, зокрема з використанням перцептронів.
Нейромережні методи прогнозування
Використовуються однокрокові і побудовані на їх основі багатокрокові нейромережні методи, в основі яких є принцип виділення в часових послідовностях так званих часових вікон – метод рухомих часових вікон.
Розглядаємо варіант однопараметричного процесу:
х0, х1, х2, х3, х4, х5, х6, х7, х8, х9, х10;
нехай розмір вхідного часового вікна:
tow=3;
х0, х1, х2 → х3.
При такому розмірі часових вікон приймається, що відлік процесу у момент часу 3 повністю визначається відліками у моменти часу 0, 1, 2; відповідно:
х1, х2, х3 → х4
х2, х3, х4 → х5
Гіпотеза про можливість отримання прогнозів підкріплена теоремою Такенса, яка стверджує, що кожен наступний відлік часової послідовності може бути передбачений з як завгодно високою точністю на підставі відомих попередніх відліків часової послідовності.
В основі теореми Такенса є той факт, що будь-які існуючі у всесвіті процеси є інерційними.
Проблеми: далеко не всі процеси можливо передбачити з задовільною точністю; іноді для точних передбачень необхідно мати нереально великі значення довжини передісторії, яка не завжди є наявною. Отже перша проблема – часто відсутність належної передісторії , або потреба у надто великих вхідних часових вікнах. Друга проблема – це труднощі у моделюванні реальної залежності типу між вхідним і вихідним вікнами.
Основи нейромережного методу рухомих часових вікон
Нехай ми маємо однопараметричний процес з наступних відліків:
х0, х1, х2, х3, х4, х5, х6│ х7, х8, х9, х10;
необхідно отримати прогнозні значення від х7 - х10.
Одно кроковий прогноз:
Використовується метод часових вікон, сформуємо вибірку даних
| Входи | Вихід | ||
| Вх. 1 | Вх. 2 | Вх. 3 | вихід |
| х0 | х1 | х2 | х3 |
| х1 | х2 | х3 | х4 |
| х2 | х3 | х4 | х5 |
| х3 | х4 | х5 | х6 |
| х4 | х5 | х6 | 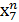
|
| х5 | х6 | 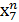
| 
|
Вибірка даних формується шляхом зсуву на одну позицію вправо до останнього відомого значення х6

Рис. 15.2. Перцептрон для одно крокового прогнозу
У даному випадку забезпечується прогноз на одну позицію вправо. Для здійснення багатокрокового прогнозу схема перцептрона була б наступною:

Рис. 15.3. Перцептрон для багатокрокового прогнозу
Реалізація варіанта 2потребує більшої передісторії, а точність навчання є гіршою ніж для варіанту 1.
Більш ефективним способом прогнозування є застосування нейромережі, яка працює зі зворотним зв’язком у циклічному режимі (Рис. 15.4).
| х6 | 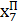
| 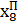
| 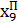
|
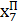
| 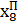
| 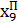
| 
|
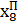
| 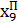
| 
| 
|
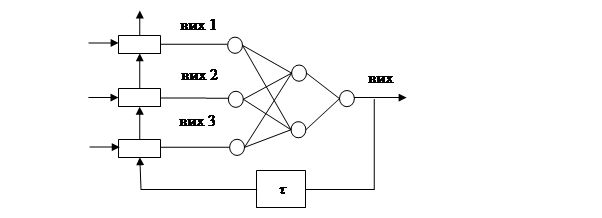
τ – елемент затримки на першому такті
Рис. 15.4. Перцептрон в циклічному режимі функціонування
Принцип функціонування
У першому такті циклічного режиму здійснюється одно крокове передбачення
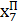 , у наступному такті передбачене значення
, у наступному такті передбачене значення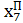 вважається точним відомим значенням і подається на вхід перциптрона. Отримуємо передбачене значення
вважається точним відомим значенням і подається на вхід перциптрона. Отримуємо передбачене значення
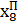 . У наступному такті
. У наступному такті 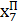 ,
, 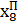 вважаємо точними значеннями, та передбачаємо значення
вважаємо точними значеннями, та передбачаємо значення 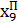 і так далі.
і так далі.
| х6 | 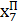
| 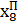
| 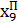
|
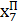
| 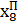
| 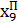
| 
|
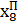
| 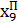
| 
| 
|
Переваги даного методу:
1. У багатьох випадках досягається великий горизонт прогнозу, який обмежується накопиченням похибок на вхід перцептрона;
2. Можна використовувати більш коротку передісторію;
3. Більш точне навчання перцептрона.
Задачі прогнозу погоди
Дані представлені у вигляді таблиці:
| день | температура | опади | тиск | сонце | |
| мм. | мм.,бр. | год. | |||
| -1 | 4,8 | 1011 | 3,8 | ||
| -1 | 2,8 | 1024 | 5,4 | ||
| … | … | … | … | … |
Реально прогнозування за довільною точністю можна забезпечити максимально на три дні вперед за умови достатньо великої навчальної вибірки. Чому не можна здійснити прогноз з більшим горизонтом?
1-а причина. Наявність прихованих параметрів, тобто прогноз здійснюється без всіх діючих факторів.
2-а причина. Неточність представлення самих параметрів (похибки вимірювань, використання усереднених величин).
Висновок: вірогідні прогнози погоди як правило здійснюються з невеликим горизонтом.
Приклад прогнозування: прогноз співвідношення валютних пар.
| Час | USD/EUR | USD/CHP | SPE/USD |
| … | … | … | |
| … | … | … |
Особливості прогнозування:
1. Підбір валютних пар здійснюється на підставі економічного аналізу, в даному випадку основна мета – прогноз співвідношення долара і євро.
2. Співвідношення долар і франк визначають певну динаміку ринку. Франк – це валюта прихисту, найбільш стабільна валюта.
3. Співвідношення долар і азіатська валюта в сучасних умовах, прогнози співвідношень валют отримати вкрай важко. Основна причина – високий рівень оснащеності засобами збору даних і прогнозу ключових гравців ринку.
Виникає фактор протидії прогнозу. Фактор протидії прогнозу існує у випадках прогнозів для соціально економічних систем.
Контрольні запитання
1. Чим пояснюється можливість робити прогнози для реально існуючих фізичних і соціальних систем?
2. Значення теореми Такенса для галузі прогнозування.
3. Існуючі методи і засоби прогнозування.
4. Поняття передісторії і горизонту прогнозування.
5. Особливість циклічного режиму перцептрона при прогнозуванні.
6. Труднощі при прогнозуванні погоди.
7. Труднощі прогнозування в соціально-економічних системах.
Лекція № 16.ШНМ зі зворотними зв’язками .
Мережа Гопфілда
Джон Гопфілд вперше представив свою асоціативну мережу у 1982 р. у Національній Академії Наук США. На честь Гопфілда та нового підходу до моделювання, ця мережна парадигма згадується як мережа Гопфілда. Мережа базується на аналогіях фізики термодинамічних систем. Початкові застосування для цього виду мережі включали асоціативну, або адресовану за змістом пам'ять та вирішували задачі оптимізації.
Мережа Гопфілда використовує три прошарки: вхідний, прошарок Гопфілда та вихідний прошарок. Кожен прошарок має однакову кількість нейронів. Входи прошарку Гопфілда під'єднані до виходів відповідних нейронів вхідного прошарку через змінні ваги з'єднань. Виходи прошарку Гопфілда під'єднуються до входів всіх нейронів прошарку Гопфілда, за винятком самого себе, а також до відповідних елементів у вихідному прошарку. В режимі функціонування, мережа скеровує дані з вхідного прошарку через фіксовані ваги з'єднань до прошарку Гопфілда. Прошарок Гопфілда коливається, поки не буде завершена певна кількість циклів, і біжучий стан прошарку передається на вихідний прошарок. Цей стан відповідає образу, вже запрограмованому у мережу.
Навчання мережі Гопфілда вимагає, щоб навчальний зразок був представлений на вхідному та вихідному прошарках одночасно. Рекурсивний характер прошарку Гопфілда забезпечує засоби корекції всіх ваг з'єднань. Недвійкова реалізація мережі повинна мати пороговий механізм у передатній функції. Для правильного навчання мережі відповідні пари "вхід-вихід" мають відрізнятися між собою.
Якщо мережа Гопфілда використовується як пам'ять, що адресується за змістом, вона має два головних обмеження. По-перше, кількість зразків, що можуть бути збережені та точно відтворені є строго обмеженою. Якщо зберігається занадто багато параметрів, мережа може збігатись до нового неіснуючого образу, відмінному від всіх запрограмованих образів, або не збігатись взагалі. Межа ємності пам'яті для мережі приблизно 15% від числа нейронів у прошарку Гопфілда. Другим обмеженням парадигми є те, що прошарок Гопфілда може стати нестабільним, якщо навчальні приклади є занадто подібними. Зразок образу вважається нестабільним, якщо він застосовується за нульовий час і мережа збігається до деякого іншого образу з навчальної множини. Ця проблема може бути вирішена вибором навчальних прикладів більш ортогональних (незалежних) між собою.
Структурна схема мережі Гопфілда приведена на рис. 16.1

Рис. 16.1. Структурна схема мережі Гопфілда.
Задача, що розв'язується даною мережею в якості асоціативної пам'яті, як правило, формулюється наступним чином. Відомий деякий набір двійкових сигналів (зображень, звукових оцифровок, інших даних, що описують певний об'єкти або характеристики процесів), вважають зразковим. Мережа повинна вміти з зашумленого сигналу, поданого на її вхід, виділити ("пригадати" по частковій інформації) відповідний зразок або "дати висновок" про те, що вхідні дані не відповідають жодному із зразків. У загальному випадку, будь-який сигнал може бути описаний вектором x1, хі, хn..., n - кількість нейронів у мережі і величина вхідних і вихідних векторів. Кожний елемент xi дорівнює або +1, або -1. Позначимо вектор, що описує k-ий зразок, через Xk, а його компоненти, відповідно, - xik, k=0, ..., m-1, m - кількість зразків. Якщо мережа розпізнає (або "пригадує") якийсь зразок на основі пред'явлених їй даних, її виходи будуть містити саме його, тобто Y = Xk, де Y - вектор вихідних значень мережі: y1, yi, yn. У протилежному випадку, вихідний вектор не співпаде з жодний зразковим.
Якщо, наприклад, сигнали являють собою якесь зображення, то, відобразивши у графічному виді дані з виходу мережі, можна буде побачити картинку, що цілком збігається з однієї зі зразкових (у випадку успіху) або ж "вільну імпровізацію" мережі (у випадку невдачі).
Алгоритм функціонування мережі
На стадії ініціалізації мережі вагові коефіцієнти синапсів встановлюються таким чином:

Тут i і j - індекси, відповідно, предсинаптичного і постсинаптичного нейронів; xik, xjk - i-ий і j-ий елементи вектора k-ого зразка.
На входи мережі подається невідомий сигнал (t - номер ітерації). Його поширення безпосередньо встановлює значення виходів: yi(0) = xi , i = 0...n-1, тому позначення на схемі мережі вхідних сигналів у явному виді носить чисто умовний характер. Нуль у дужках справа yi означає нульову ітерацію в циклі роботи мережі.
Розраховується новий стан нейронів
 , j=0...n-1
, j=0...n-1
і нові значення виходів

де f - передатна функція у виді порогової, приведена на рис. 16.2.

Рис. 16.2. Передатні функції
Перевіряємо чи змінилися вихідні значення виходів за останню ітерацію. Якщо так - перехід до пункту 2, інакше (якщо виходи стабілізувались) - кінець. При цьому вихідний вектор являє собою зразок, що найкраще відповідає вхідним даним.
Іноді мережа не може провести розпізнавання і видає на виході неіснуючий зразок. Це пов'язано з проблемою обмеженості можливостей мережі. Для мережі Гопфілда кількість образів , що запам’ятовуються, не повинно перевищувати величини, приблизно рівної 0.15•n. Крім того, якщо два зразки А и Б сильно схожі, вони, можливо, будуть викликати в мережі перехресні асоціації, тобто пред'явлення на входи мережі вектора А призведе до появи на її виходах вектори Б и навпаки.
Двоскерована асоціативна пам’ять
Ця мережна модель була розроблена Бартом Козко (Bart Kosko) і розширює модель Гопфілда. Множина парних образів навчається за образами, що представлені як біполярні вектори. Подібно до мережі Гопфілда, коли представляється зашумлена версія одного образу, визначається найближчий зразок, асоційований з ним.
На рис. 10.3 показаний приклад двоскерованої асоціативної пам'яті. Вона має стільки входів, скільки є вихідних нейронів. Два приховані прошарки містяться на двох окремих асоціативних елементах пам'яті і представляють подвоєний розмір вхідних векторів. Середні прошарки повністю з'єднуються один з одним. Вхідний та вихідний прошарки потрібні для реалізації засобів введення та відновлення інформації з мережі.
Середні прошарки розроблені для збереження асоційованих пар векторів. Коли зашумлений вектор образу вважається вхідним, середні прошарки коливаються до досягнення стабільного стану рівноваги, який відповідає найближчій навченій асоціації і буде генерувати початковий навчальний зразок на виході. Подібно до мережі Гопфілда, двоскерована асоціативна пам'ять є схильною до неправильного відшукування навченого образу, якщо надходить невідомий вхідний вектор, який не був у складі навчальної множини.
Двоскерована асоціативна пам'ять відноситься до гетероасоціативної пам'яті. Вхідний вектор надходить на один набір нейронів, а відповідний вихідний вектор продукується на іншому наборі нейронів. Вхідні образи асоціюються з вихідними. Для порівняння: мережа Гопфілда є автоасоціативною. Вхідний зразок може бути відновлений чи виправлений мережею, але не може бути асоційований з іншим зразком. У мережі Гопфілда використовується одношарова структура асоціативної пам'яті, у якій вихідний вектор з'являється на виході тих же нейронів, на які надходить вхідний вектор.
Двоскерована асоціативна пам'ять, як і мережа Гопфілда, здатна до узагальнення, виробляючи правильні вихідні сигнали, незважаючи на спотворені входи.
Розглянемо схему двоскерованої асоціативної пам'яті. Вхідний вектор A обробляється матрицею ваг W мережі, у результаті чого продукується вектор вихідних сигналів мережі B. Вектор B обробляється транспонованою матрицею WT ваг мережі, яка продукує сигнали, що представляють новий вхідний вектор A. Цей процес повторюється доти, поки мережа не досягне стабільного стану, у якому ні вектор A, ні вектор B не змінюються. Для порівняння: мережа Гопфілда є автоасоціативною. Вхідний зразок може бути відновлений чи виправлений мережею, але не може бути асоційований з іншим зразком. У мережі Гопфілда використовується одношарова структура асоціативної пам'яті, у якій вихідний вектор з'являється на виході тих же нейронів, на які надходить вхідний вектор.
Двоскерована асоціативна пам'ять, як і мережа Гопфілда, здатна до узагальнення, виробляючи правильні вихідні сигнали, незважаючи на спотворені входи.
Розглянемо схему двоскерованої асоціативної пам'яті. Вхідний вектор A обробляється матрицею ваг W мережі, у результаті чого продукується вектор вихідних сигналів мережі B. Вектор B обробляється транспонованою матрицею WT ваг мережі, яка продукує сигнали, що представляють новий вхідний вектор A. Цей процес повторюється доти, поки мережа не досягне стабільного стану, у якому ні вектор A, ні вектор B не змінюються.

Рис. 16.3. Двоскерована асоціативна пам'ять
Нейрони в прошарках 1 і 2 функціонують, як і в інших парадигмах, обчислюючи суму зважених входів і значення передатної функції F:
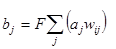
або у векторній формі:
B=F(AW)
де B - вектор вихідних сигналів нейронів прошарку 2, A - вектор вихідних сигналів нейронів прошарку 1, W - матриця ваг зв'язків між прошарками 1 і 2, F - передатна функція.
Аналогічно A=F(BWT), де WT є транспонованою матрицею W.
В якості передатної функції використовується експонент та сигмоїда.
Прошарок 0 не робить обчислень і не має пам'яті. Він є лише засобом розподілу вихідних сигналів прошарку 2 до елементів матриці WT.
Формула для обчислення значень синаптичних ваг:
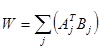
де Aj і Bj - вхідні і вихідні сигнали навчальної вибірки.
Вагова матриця обчислюється як сума добутків всіх векторних пар навчальної вибірки.
Системи зі зворотним зв'язком мають тенденцію до коливань. Вони можуть переходити від стану до стану, ніколи не досягаючи стабільності. Доведено, що двоскерована асоціативна пам'ять безумовно стабільна при будь-яких значеннях ваг мережі.
Області застосування. Асоціативна пам'ять, розпізнавання зразків.
Недоліки. Ємність двоскерованої асоціативної пам'яті жорстко обмежена. Якщо n - кількість нейронів у вхідному прошарку, то кількість векторів, що можуть бути запам'ятовані в мережі не перевищує L=n/2log2n. Так, якщо n=1024, то мережа здатна запам'ятати не більш 25 зразків.
Двоскерована асоціативна пам'ять має деяку непередбачуваність у процесі функціонування, можливі помилкові відповіді.
Переваги.
У порівнянні з автоасоціативною пам'яттю (наприклад, мережею Гопфілда), двоскерована асоціативна пам'ять дає можливість будувати асоціації між векторами A і B, що у загальному випадку мають різні розмірності. За рахунок таких можливостей гетероасоціативна пам'ять має більш широкий клас застосувань, ніж автоасоціативна пам'ять.
Двоскерована асоціативна пам'ять - проста мережа, що може бути реалізована у виді окремої НВІС чи оптоелектронним способом.
Процес формування синаптичних ваг простий і швидкий. Мережа швидко збігається в процесі функціонування.
Модифікації.
Сигнали в мережі можуть бути як дискретними, так і аналоговими. Для обох випадків доведена стабільність мережі. Були запропоновані моделі двоскерованої асоціативної пам'яті з навчанням без вчителя (адаптивна двоскерована асоціативна пам'ять). Введення латеральних зв'язків всередині прошарку дає можливість реалізувати конкуруючу двоскеровану асоціативну пам'ять.
Контрольні запитання
1. Основні відмінності топологій БШП та ШНМ Гопфілда.
2. Особливості навчання ШНМ Гопфілда в порівнянні з навчанням БШП.
3. Області застосування ШНМ Гопфілда.
4. Фізичні аналогії для ШНМ Гопфіода.
5. Обмеження ШНМ Гопфілда.
6. Відмінності двоскерованої асоціативної пам’яті від ШНМ Гопфілда.
7. Призначення двоскерованої асоціативної пам’яті.
Лекція № 17.ШНМ з нейронними елементами радіального типу.
Мережа з радіальними базовими функціями в найбільш простій формі – це мережа з трьома шарами: звичайним вхідним шаром, який виконує розподілення даних зразка для першого прошарку ваг, прихованим і вихідним прошарками. Відображення від вхідного прошарку до схованого прошарку є нелінійним, а відображення прихованого прошарку у вихідний - лінійне. Звичайно (але не завжди) кількість прихованих елементів більше кількості вхідних елементів. Ідея полягає у тому, що якщо нелінійну проблему розмістити в просторі збільшеної розмірності деяким нелінійним чином, то імовірність того, що вона буде лінійно розділимою, виявляється вищою.
Розглянемо відображення першого прошарку. З кожним прихованим елементом пов'язується деяка функція  . Кожна з цих функцій має комбінований вхід і породжує значення активності, що подається на вихід. Сукупність значень активності всіх прихованих елементів визначає вектор, на який відображається вхідний вектор:
. Кожна з цих функцій має комбінований вхід і породжує значення активності, що подається на вихід. Сукупність значень активності всіх прихованих елементів визначає вектор, на який відображається вхідний вектор:
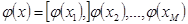 ,
,
де М позначена кількість прихованих елементів, а х — вхідний вектор.
Зв'язки елемента прихованого прошарку визначають центр радіальної функції для даного прихованого елемента. Вхід для кожного елемента вибирається рівним евклідовій нормі:
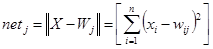
де n позначено кількість вхідних елементів.
Для прихованих елементів використовують самі найрізноманітніші функції активації, наприклад, функцію Гауса  або функцію
або функцію 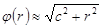 . Нейронний елемент Гаусівського типу показаний на рис. 17.1.
. Нейронний елемент Гаусівського типу показаний на рис. 17.1.

Рис. 17.1. Нейронний елемент гаусівського типу
Оператор R здійснює обчислення евклідової віддалі до центру RBF – опорної точки, яка відповідає даному нейронному елементу, f – обчислення Гаусівської функції
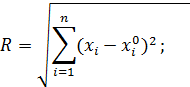
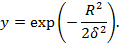
Форма гасівської функції активації показана на рис. 11.2. Чим більша величина δ, тим функція пологіша.
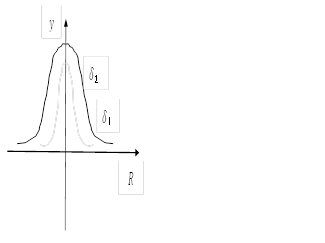
Рис. 11.2. Гаусівська функція активації
У випадку якщо вхідні вектори пронормовані до одиничного радіусу
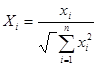 , то оператор R набуває вигляду
, то оператор R набуває вигляду 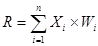
і буде відрізнятись від класичного формального нейрона лише гаусівською функцією активації.
Структура нейромереж радіальних базових функцій

Входами нейромережі RBF є x1, x2, x3. Наступним є шар нейронних елементів з гаусівськими функціями активації, кожен з нейронів відповідає центру радіальної функції. Кожен центр визначається своїми координатами (x1і, x2і, … x3і) у випадку, якщо вхідний вектор співпадає з координатам центру, то на виході нейронного елемента маємо сигнал 1.
Вихідним каскадом нейромережі може бути може бути також інша нейромережа, зокрема одношаровий перцептрон.
Питання, які необхідно вирішувати для налагодження і навчання нейромережі RBF.
1. Вибір центрів радіальних функцій, як правило число центрів більше n.
m>n
Найпростіше центри представляють собою випадкову вибірку з векторів тренувальних даних. В якості центрів обираються центри кластерів вхідних даних. Для кластеризації можна застосувати будь-який відомий алгоритм кластеризації, в тому числі само організаційну карту особливостей карт Коганена, як перший каскад .
2. Вибір  яка є параметром розмаху гаусівської функції
яка є параметром розмаху гаусівської функції
Найпростіший варіант – вибирати спільне  для всіх центрів RBF. При нерівномірному представленні даних такий вибір не забезпечує необхідну точність. Для підвищення точності застосовують метод k «наближчих сусідів» - KNN, Метод передбачає для кожної точки вибірки даних обчислення віддалей до k найближчих точок.
для всіх центрів RBF. При нерівномірному представленні даних такий вибір не забезпечує необхідну точність. Для підвищення точності застосовують метод k «наближчих сусідів» - KNN, Метод передбачає для кожної точки вибірки даних обчислення віддалей до k найближчих точок.  обирається пропорційною до середньої віддалі до цих точок.
обирається пропорційною до середньої віддалі до цих точок.
Порівняння нейромережних RBF і багатошарових перцептронів
1. RBF мережі забезпечують більшу швидкість навчання і простіше налагодження.
2. RBF мережі дозволяють моделювати поверхні відгуку довільної складності;
3. На відмінну від багатошарових перцептронів мережі RBF не володіють здатністю до екстраполяції даних (якщо точка виходить за межі навчальної вибірки, то результат буде мати низьку точність).
Як спрощений варіант ШНМ RBF розглядають імовірнісні ШНМ і ШНМ узагальненої регресії.
Імовірнісна нейромережа ( PNN – probabilistic neural network) належить до нейромереж з швидким навчанням, але достатньо великими часовими затримками при функціонуванні. Виходи такої мережі можна інтерпретувати, як оцінки ймовірності належності елементу певному класу. Ймовірнісна мережа вчиться оцінювати функцію густини ймовірності, її вихід розглядається як очікуване значення моделі в даній точці простору входів.
При рішенні задач класифікації оцінюється густину ймовірності для кожного класу, порівнюються між собою ймовірності приналежності до різних класів і обирається варіант, для якого густина ймовірності буде найбільшою. Оцінка густини ймовірності в мережі заснована на ядерних оцінках. Якщо приклад розташований в даній точці простору, тоді в цій точці є певна густина ймовірності. Кластери з близько розташованих точок, свідчать, що в цьому місці густина ймовірності велика. Поблизу спостереження є більша довіра до рівня густини, а по мірі віддалення від нього довіра зменшується і плине до нуля. В методі ядерних оцінок в точку, що відповідає кожному прикладу, поміщається деяка проста функція, потім вони всі додаються і в результаті утворюється оцінка для загальної густини ймовірності. Найчастіше в якості ядерних функцій беруть дзвоноподібні функції (гаусові). Якщо є достатня кількість навчальних прикладів, такий метод дає добрі наближення до істинної. Ймовірнісна мережа має три прошарки: вхідний, радіальний та вихідний. Радіальні елементи беруться по одному на кожний приклад. Кожний з них містить гаусову функцію з центром в цьому прикладі. Кожному класу відповідає один вихідний елемент. Вихідний елемент з'єднаний лише з радіальними елементами, що відносяться до його класу і підсумовує виходи всіх елементів, що належать до його класу. Значення вихідних сигналів утворюються пропорційно ядерних оцінок ймовірності приналежності відповідним класам.
Ймовірнісна мережа має три прошарки: вхідний, радіальний та вихідний. Радіальні елементи беруться по одному на кожний приклад. Кожний з них містить гаусову функцію з центром в цьому прикладі. Кожному класу відповідає один вихідний елемент. Вихідний елемент з'єднаний лише з радіальними елементами, що відносяться до його класу і підсумовує виходи всіх елементів, що належать до його класу. Значення вихідних сигналів утворюються пропорційно ядерних оцінок ймовірності приналежності відповідним класам.
1. Маємо тренувальну вибірку з к+m векторів. Нехай к векторів вибірки 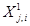 , де j=1,…,к – номер вектора, i=1,…,n – номер компоненти вектора представляють перший клас об’єктів, що підлягають класифікації;; всі інші m векторів, що не належать класу 1, відносимо до класу 2. На вхід нейромережі надходить вхідний вектор
, де j=1,…,к – номер вектора, i=1,…,n – номер компоненти вектора представляють перший клас об’єктів, що підлягають класифікації;; всі інші m векторів, що не належать класу 1, відносимо до класу 2. На вхід нейромережі надходить вхідний вектор  , який необхідно класифікувати, тобто встановити імовірність його належності до класу 1.
, який необхідно класифікувати, тобто встановити імовірність його належності до класу 1.
2. Знаходимо евклідові віддалі вхідного вектора до векторів тренувальної вибірки класів 1 і 2. 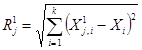 ,
,  .
.
3. Переходимо від них до гаусівських віддалей 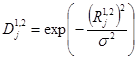 , де
, де  - коефіцієнт розмаху функції, що підбирається експериментально.
- коефіцієнт розмаху функції, що підбирається експериментально.
4. Імовірність належності вхідного вектора до класу 1 обчислюється за формулою  . P(1) завжди не перевищує 1, так як сума Р(1)+Р(2) =1.
. P(1) завжди не перевищує 1, так як сума Р(1)+Р(2) =1.
Нейронна мережа узагальненої регресії (GRNN - General Regression Neural Network) має багато аналогій з імовірнісною нейромережею PNN. Однак основне її призначення – розвязок завдань регресії, зокрема передбачення, прогнозування часових послідовностей.
Подібно до імовірнісної мережа GRNN має три прошарки: вхідний, радіальний та вихідний. Радіальні елементи беруться по одному на кожний приклад. Кожний з них містить гаусову функцію з центром в цьому прикладі. Кожному класу відповідає один вихідний елемент. Вихідний елемент з'єднаний лише з радіальними елементами, що відносяться до його класу і підсумовує виходи всіх елементів, що належать до його класу. Значення вихідних сигналів утворюються пропорційно ядерних оцінок ймовірності приналежності відповідним класам.
1. Маємо тренувальну вибірку з m векторів. Кожен вектор містить набір вхідних (завжди відомих компонентів)  , де j=1,…,m – номер вектора, i=1,…,n – номер компоненти вектора та вихідну компоненту
, де j=1,…,m – номер вектора, i=1,…,n – номер компоненти вектора та вихідну компоненту  , яка відома лише для векторів тренувальної вибірки.
, яка відома лише для векторів тренувальної вибірки.
2. Метою нейромережі є передбачення вихідної компоненти  для заданого вхідних компонентів вектора
для заданого вхідних компонентів вектора  .
.
3. Знаходимо евклідові віддалі вхідного вектора до всіх векторів тренувальної вибірки.  .
.
4. Переходимо від них до гаусівських віддалей  , де
, де  - коефіцієнт розмаху функції, що підбирається експериментально.
- коефіцієнт розмаху функції, що підбирається експериментально.
5. Оцінка шуканої вихідної компоненти знаходимо за формулою 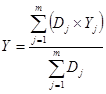 .
.
Контрольні запитання
1. Топологічні особливості ШНМ RBF.
2. Порівняння БШП і ШНМ RBF.
3. Особливості функцій активації ШНМ RBF.
4. Особливості навчання ШНМ RBF.
5. Недоліки і переваги ШНМ RBF.
6. Особливості і призначення імовірнісних ШНМ.
7. Особливості і призначення ШНМ узагальненої регресії.
Лекція №18.ШНМ геометричних перетворень.
В основі моделювання за допомогою нейроподібних структур геометричних перетворень (ГП) є базовий принцип представлення гіперповерхонь відгуків в ортогональних системах координат ( як прямолінійних, так і криволінійних) моделі, які максимально співпадають з основними вимірами гіперповерхонь. В якості близького аналога нейроподібних структур ГП можна розглянути двошаровий перцептрон автоасоціативного типу, побудований за методом „звуженого горла“ (рис.1). На входи перцептрона подаються одночасно всі компоненти наявних векторів вибірки, ці ж компоненти повторюються як вихідні сигнали тренувальних векторів перцептрона для здійснення навчання. В загальному випадку „звуженого горла“, коли число нейронних елементів прихованого шару менше за число входів (виходів) перетворення вхідних векторів у ідентичні їм вихідні відбувається з певною похибкою. Вихідні сигнали нейронних елементів відображають сигнали головних компонентів. Внаслідок застосування оптимізаційних процедур навчання похибка перетворень вхідних векторів у ідентичні їм вихідні мінімізується, а вихідні сигнали нейронних елементів прихованого шару задають оптимізоване представлення вхідних векторів у новій системі координат зменшеної розмірності. Якщо вхідний вектор автоасоціативної нейромережі включає в себе сигнали вхідних змінних і сигнали відгуків, а число нейронних елементів прихованого шару відповідає розмірності простору еліпсоїда розсіювання, то на виході мережі поверхні відгуків апроксимуються гіперплощинами (площинами), а величини додаткових вимірів представляють похибки такої апроксимації.

Рис.1. НС ГП автоасоціативного типу
Базовим режимом ГП є автоасоціативний режим функціонування. Однак існують суттєві відмінності нейроподібних автоасоціативних структур ГП від багатошарових перцептронів в автоасоціативному варіанті застосування. Основна відмінність полягає в тому, що режим „звуженого горла“ не є обов’язковим для реалізації подібних структур, отже, існує можливість точного (з нульовою методичною похибкою) відображення векторів вхідних сигналів у вектори вихідних, одночасно виділяючи на виходах нейронних елементів прихованого шару сигнали всіх компонентів інформаційного об’єкта. Причому, перша компонента задає напрямок, вздовж якого дисперсія максимальна, наступна компонента проводиться таким чином, що вздовж неї максимізується залишкова варіація і т.д. Достатньо близьким, через виділення головних компонентів, є також режим відображення відгуків на підставі заданих входів (проективна задача), так як існує взаємно однозначна відповідність між координатами точок еліпсоїду розсіювання входів та гіпертіла. На підставі єдиного підходу розв’язуються також задачі ущільнення даних, факторного аналізу, кластеризації в режимі самонавчання, фільтрації сигналів та ін.
Особливості навчання. В автоасоціативному режимі моделей ГП послідовні кроки перетворень гіпертіла реалізуються шляхом проектування його на ортогональні гіперплощини, що проходять через початок координат, починаючи з вимірності n і аж до нульової вимірності. Даний режим забезпечує розв’язок завдань ущільнення даних, факторного аналізу, кластеризації, фільтрації; функції відновлення пропущених табличних даних для даного режиму, включаючи невідомі відгуки, забезпечуються введенням циклічного зворотного зв’язку.
Режим відображення заданих входів у невідомі відгуки виконується шляхом покрокових геометричних перетворень в (n+1)-вимірному просторі реалізацій, де n – число незалежних входів моделі; на першому кроці перетворень визначається найдовша вісь еліпсоїда розсіювання, яка співпадатиме з першою координатою входів на еліпсоїді; апроксимуємо гіперповерхні відгуку (кожну з них окремо) елементарною гіперповерхнею від першої координати входів; отримуємо залишок такої апроксимації, як різницю вихідних координат гіперповерхні і елементарної апроксимуючої гіперповерхні; вимірність задачі скоротилася на одиницю; на другому кроці визначаємо наступну за розміром вісь еліпсоїда (друга координата входів); апроксимуємо залишок від попереднього кроку апроксимації елементарною гіперповерхнею від другої координати входів; число кроків перетворень не перевищує n; результатами навчання є параметри системи координат входів на еліпсоїді та параметри моделей елементарних гіперповерхонь для кожного кроку перетворень.
Функціонування. Як і в попередньому випадку реалізується покроково, де на першому кроці вектор входів перетворюється в першу координату входів на еліпсоїді розсіювання (згідно напрямку найдовшої осі, отриманої при навчанні), для даної координати знаходиться відгук на першій елементарній гіперповерхні далі знаходиться відгук для другої координати входів на еліпсоїді і т.д. Шуканий відгук обчислюється як зважена сума відгуків, отриманих на елементарних поверхнях.
Особливості розв’язку лінійних задач. Гіперповерхні відгуку є гіперплощинами, додатковий вимір моделі повністю визначається шумовими компонентами та похибками заокруглень. Результати застосування ГП – основні виміри гіперплощини співпадають з результатами отриманими за допомогою відомих методів РСА. Однак, застосування ГП надає ряд переваг, зокрема, даний метод швидкий, неітеративний, без накопичення похибок і помітних обмежень на вимірність; відпадає потреба в розв’язках систем нормальних рівнянь, або у здійсненні ітеративної адаптації.
Для гладких нелінійних залежностей ГП забезпечує побудову криволінійної ортогональної системи координат моделі, виділення нелінійних головних компонентів, близьких до незалежних.
В режимі застосування навченої моделі ГП існує принципова можливість аналізу координат (компонентів моделі) на передбачуваність та вилучення шумових компонент.
В найпростішому випадку, вважаючи дані координати незалежними, аналіз виконується шляхом покрокової оцінки змін похибок в режимі застосування і маскування компонентів, що сприяють збільшенню похибок.
В модусі прогнозування часових послідовностей забезпечується об’єктивне виділення та аналіз всіх незалежних трендів, що представляють послідовність, де кількість трендів рівна розміру обраного вхідного часового вікна.
В багатьох задачах еліпсоїд розсіювання виявляється суттєво “сплюснутим” по багатьох напрямках, отже даними координатами входів можна знехтувати. Це зменшує вимоги до необхідного об’єму тренувальною вибірки. Для надмалих тренувальних вибірок, в .т.ч. коли число векторів менше числа первинних входів, можна обмежитися лише декількома “найдовшими” координатами входів на еліпсоїді – основними факторами і отримати можливість здійснювати навчання і генералізацію на основі врахування лише цих факторів. Класичні методи передбачення в подібних випадках не забезпечать отримання жодної корисної інформації.
Особливості розв’язування суттєво нелінійних задач. Застосовується режим, що забезпечує перетворення первинних входів у радіальні базові функції. Відбувається лінеаризація задачі, однак відомі варіанти RBF та гібридних мереж мають суттєві недоліки: погана генералізація, відсутність екстраполяційних властивостей, потреба у великих тренувальних вибірках.
Застосування RBF методу на основі ГП, включаючи детерміновану повторюваність розташування центрів RBF на основі виділених головних компонентів, повністю знімає перелічені недоліки. Це стає можливим за рахунок відкидання малозначимих та шумових компонентів, селекції необхідних компонентів відповідно до тренувальної та тестової вибірок. В результаті забезпечується поєднання властивості відтворювати складні нелінійні залежності та здатність до генералізації в умовах існуючих вибірок даних; додатково створюються умови для візуалізації даних в координатах обраних компонентів.
Лекція № 19.Основи нечіткої логіки.
Нечітка логіка презентує специфічний розділ м’яких обчислень, до якого також відносять штучні нейромережі, генетичні алгоритми, імовірнісні (байесівські методи). Вважається, що м’які обчислення ефективні для задач моделювання складних систем, або керування складними системами в умовах невизначеності.
Етапи розвитку нечіткої логіки.
Поштовх до появи нечіткої логіки пов’язують зі створенням квантової теорії, в основі якої є принцип невизначеності. За відкриття принципу невизначеності у 1932 році Гейзенбергу присудили Нобелівську премію. Принцип невизначеності привів до появи багатозначної логіки. Межами невизначеності є:
- TRUE;
- FALSE.
Таким чином у граничному випадку нечітка логіка зводиться до булевої алгебри.
І етап. Англійський вчений М. Блек першим ввів поняття неперервної логіки, яку застосував до множин елементів і символів.
ІІ етап. Цей етап безпосередньо пов'язаний з Лотфі Заде, якого вважають творцем нечіткої логіки. У 1965 р. ним опублікувана фундаментальна праця «Нечіткі множини», де викладено низку важливих принципів. Принцип несумісності – чим складніша система, тим менша здатність давати точні і одночасно практичні судження про її поведінку, тобто після деякого порогу точність і практичний зміст взаємовиключаються.
Основні положення теорії Лотфі Заде
1. Вводиться поняття лінгвістичних змінних.
2. Відношення між змінними описується нечіткими висловлюваннями;
3. Складне відношення між змінними описується нечіткими алгоритмами.
ІІІ етап. Поява комерційних продуктів. У 1987 році японцями був продемонстрований швидкісний потяг у місті Сендай, де використовувалось автоматичне управління на базі нечіткої логіки. Крім цих пристроїв почали широко використовуватися контролери для автоматичного виробництва, а також системи військового призначення.

Рис. 18.1. Загальна структура функціонування систем нечіткої логіки
Системи м’яких обчислень функціонують за принципом: на вхід ми отримуємо дані у просторі вхідних ознак. Мета – отримання вихідних даних у просторі вихідних ознак. Відображення з одного простору в інший не може бути здійснено за допомогою математичної моделі, так як проблема відображення ускладнюється наявністю невизначеностей різноманітного походження. При використанні штучних нейромереж відображення здійснюються за допомогою засобів під назвою чорна скринька (є вхідні і вихідні дані, а принцип перетворення залишається закритим). Нечітка логіка функціонує за принципом – напівпрозора скринька, або прозора скринька, де відомо на основі яких міркувань вхідні дані перетворюються у вихідні.
Особливості систем нечіткої логіки.
1. Прозорість для користувача.
2. Нечутливість до неточності вхідних даних, але і одночасно невисока точність.
3. Здатність моделювати складні нелінійні зв’язки.
4. Дозволяє враховувати досвід кваліфікованих експертів, який часто базується на інтуїції. В основі побудови систем – природна мова спілкування людей.

Рис. 18.2. Два основні напрямки побудови систем нечіткої логіки
Реляційні нечіткі системи – вхідні нечіткі змінні відображаються на вихідні при допомозі нечітких відношень, наприклад, реляційними матрицями. Продукційні нечіткі системи – в основі множина окремих продукційних правил для визначення ступеня істинності передумов.
Поняття нечітких множин
Нехай Е - універсальна множина, х – елемент множини
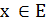 ;
;
R – деяка властивість; чітка підмножина А, А 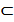 R, елементи якої задовольняють властивості R, визначається як множина впорядкованих пар
R, елементи якої задовольняють властивості R, визначається як множина впорядкованих пар
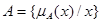 ,де
,де
 - функція належності х, вона приймає значення з множини М, наприклад М = [0,1].
- функція належності х, вона приймає значення з множини М, наприклад М = [0,1].
Випадок чіткої множини відображається наступним графіком. Функція належності приймає значення 0 або 1.

Функція R належності має значення (0, 1). Задача: розділити особи по біологічному віку. Для нечіткої множини функція належності приймає значення інтервалу від 0 до 1.
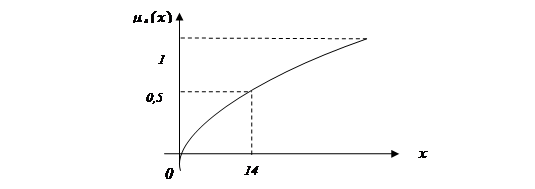
Операції над множинами
Основні операції над множинами:
1. Включення А⊂В. Неч
Читайте також:
- Відмова у прийнятті позовної заяви та повернення без розгляду
- Градієнтний метод із дробленням кроку
- З наступним поверненням до
- Земля як елемент електричної мережі. Напруга кроку
- Кредит — це система відносин з приводу акумуляції та використання тимчасово вільних грошових засобів на основі повернення та платності у формі позичкового відсотка.
- Методика вибору кроку по часу при детерміністичному моделюванні.
- Напруга кроку та дотику.
- Напруга кроку.
- Напруга кроку.
- Небезпека напруг дотику та кроку.
- Облік наданих знижок, повернення товарів та ПДВ
- Облік операцій з повернення раніше списаної безнадійної заборгованості за основним кредитним боргом та нарахованими процентними доходами
| <== попередня сторінка | | | наступна сторінка ==> |
| Варіаційні ряди та їх характеристики | | | Електроенергетика |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |