• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Закон повного струму. Використання закону повного струму для розрахунку магнетного поля

Закон повного струму. Використання закону повного струму для розрахунку магнетного поля.

13.2. Магнетний потік. Теорема Гаусса для магнетного поля.

13.3. Робота переміщення провідника із струмом і контуру із струмом у магнетному полі.

13.4. Енергія магнетного поля.

Скористаємось рівнянням Максвелла для циркуляції вектора напруженості магнетного поля

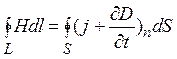, (13.1.1)

де j – густина струму провідності вільних електричних зарядів; 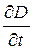- струм зміщення, не пов’язаний з наявністю вільних електричних зарядів; Н – напруженість магнетного поля.

У провідниках, в яких є вільні електричні заряди, струм зміщення відсутній (він може існувати лише у діелектричному середовищі), тобто

.

У цьому випадку рівняння (13.1.1) набуває вигляду:

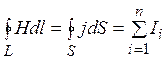. (13.1.2)

Рівняння (13.1.2) називається законом повного струму. Для написання закону повного струму через індукцію магнетного поля слід замінити Н у формулі (13.1.2) на

.

Закон повного струму у цьому випадку матиме вигляд

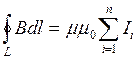. (13.1.3)

Рівняння (13.1.3) формулюється так:

Циркуляція вектора індукції магнетного поля уздовж довільного замкнутого контуру дорівнює алгебраїчній сумі всіх струмів, охоплених цим контуром і помноженій на mm₀.

Як видно з рівняння (13.1.3)

.

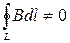Таке магнітне поле називається вихровим. Силові лінії магнетного поля є завжди замкнутими.

Скористаємось законом повного струму (13.1.3) для розрахунку магнетного поля соленоїда і тороїда.

а) знайдемо циркуляцію вектора В вздовж замкнутого контуру ABCD (рис.13.1). У нашому випадку витки в соленоїді щільно прилягають один до одного. Соленоїд має довжину, значно більшу за діаметр.

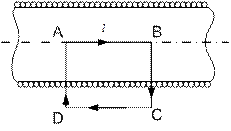
Рис.13.1

.

На ділянках DA і BC 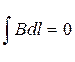; Тут а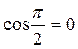

На ділянці CD ; Цю ділянку можна вибрати досить далеко від соленоїда, де магнетне поле відсутнє.

Тому з урахуванням цих зауважень маємо:

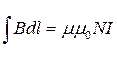. (13.1.4)

де N – число витків, які вкладаються в інтервалі довжини соленоїда АВ; І – струм, який протікає в цих витках.

Але 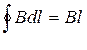, де l = AB. Закон повного струму в цьому випадку перепишеться:

. (13.1.5)

Звідки індукція магнетного поля на осі довгого соленоїда буде дорівнювати:

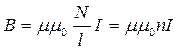. (13.1.6)

Вираз (13.1.6) показує, що на осі довгого соленоїда зі струмом І індукція магнетного поля дорівнює:

В = mm₀nI.

б) магнітне поле на осі тороїда.

Розглянемо тороїд, який має вигляд довгого соленоїда, кінець і початок якого збігаються (рис.13.2).

Рис.13.2

Витки в такій котушці щільно прилягають один до одного, а радіус осьової лінії R. Знайдемо циркуляцію вектора 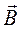вздовж осьової лінії тороїда

,

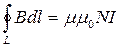де N - число витків у тороїді; І - струм у витках.

Але 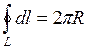- довжина кола вздовж осьової лінії, тому

,

де - число витків на одиницю довжини осьової лінії тороїда.

Таким чином, індукція магнетного поля на осі тороїда визначається такою ж формулою, що і для довгого соленоїда, тобто

В = mm₀nI . (13.1.7)

13.2. Магнетний потік. Теорема Гаусса для магнетного поля

Потоком магнетної індукції або магнетним потоком називають скалярну величину, яка дорівнює:

, (13.2.1)

де - вектор індукції магнетного поля у напрямку нормалі до площадки dS (рис.13.3)

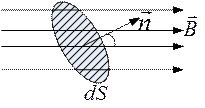
Рис.13.3

Повний магнетний потік через поверхню S знаходять шляхом інтегрування.

Розмірність магнетного потоку визначається так:

[Ф] = [В]×[S] = Тл×м² = Вб.

Магнетному потоку в 1 Вб відповідає 10⁸ силових ліній індукції магнітного поля крізь площадку в 1 м².

У випадку замкнутої поверхні слід відрізняти між собою такі особливості:

- силові лінії, які входять у поверхню, мають від’ємний потік, тому в цьому випадку

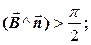
- силові лінії, які виходять з поверхні мають

- у загальному випадку

. (13.2.2)

Вираз (13.2.2) є теоремою Гаусса для магнетного поля. Суть цієї теореми полягає в тому, що силові лінії магнетного поля не пов’язані з магнетними зарядами. Магнетних зарядів у природі не існує. Описане явище показане на рис. 13.4.

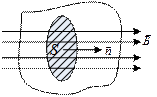
Рис.13.4

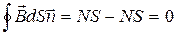. (13.2.3)

13.3. Робота переміщення провідника із струмом і контуру із струмом у магнетному полі

Знайдемо роботу, яку слід виконати для переміщення провідника із струмом І у магнетному полі, як це показано на рис. 13.5

Рис.13.5

Провідник, що має довжину l і струм І виготовлений у вигляді коточка і має можливість переміщуватись. На рухому частину провідника з сторони магнетного поля діє сила Ампера, напрям якої визначається правилом лівої руки.

Для переміщення такого коточка вздовж направляючих дротів слід прикладати силу F, яка має бути рівною силі Ампера. Робота в цьому випадку буде дорівнювати:

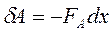. (13.3.1)

де F_A=IBl – величина сили Ампера, яка діє на рухомий коточок, тому:

dA = -Ibldx = -IbdS = -IdF (13.3.2)

Знак мінус показує, що робота виконується проти сили Ампера.

Якщо роботу виконує сила Ампера, то

dA= IdF (13.3.3)

де dА – позитивна робота, виконана силою Ампера.

Після інтегрування одержуємо роботу сили по переміщенню провідника із струмом у магнетному полі.

A = -IDF,

або

A =IDF. (13.3.4)

У випадку контуру із струмом, який рухається у магнетному полі, слід враховувати як позитивну роботу, так і негативну роботу переміщення двох частин цього контуру (рис.13.6)

Рис.13.6

При русі частини контуру АС (зліва) робота виконується позитивна. Тому в цьому випадку

dA₁ = I(dF₁ + dF₀), (13.3.5)

де dФ₁ – потік, який визначається площею лівої частини контуру АС (заштрихована площа),

dФ₀ - потік, який визначається площею самого контуру з струмом.

При переміщенні правої сторони цього контуру робота буде дорівнювати

dA₂ = -I(dF₂ + dF₀), (13.3.6)

де dФ₂ – потік, який утвориться переміщенням правої частини контуру; dФ₀ – потік за рахунок площі самого контуру.

Ця площа перекривається площею правої сторони контуру. Робота dА₂ – від’ємна.

У загальному випадку робота переміщення контуру з струмом у магнетному полі буде дорівнювати

dA = I(dF₁ - dF₂)= IdF. (13.3.7)

Після інтегрування одержимо

А=ІDФ. (13.3.8)

Висновок. Робота переміщення провідника із струмом і контуру із струмом визначається однаковою формулою.

13.4. Енергія магнетного поля

Розглянемо замкнуте коло, в якому є резистор R, котушка L і джерело струму e (рис.13.7)

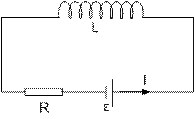
Рис.13.7

Скористаємось другим правилом Кірхгофа для замкнутого контуру, показаного на рис.13.7.

У цьому випадку

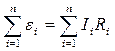, (13.4.1)

або

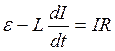, (13.4.2)

де 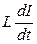- електрорушійна сила самоіндукції, діє лише в момент замикання або розмикання кола.

З рівняння (13.4.2) визначимо електрорушійну силу джерела

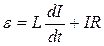. (13.4.3)

Зведемо цей вираз до спільного знаменника

edt = Irdt + LdI . (13.4.4)

Помножимо вираз (13.4.4) на струм І, одержимо

Iedt = I²rdt + LIdI , (13.4.5)

де I²rdt - джоулевe тепло; Iedt - робота сторонніх сил джерела струму; LIdI - енергія магнетного поля, локалізована в котушці зі струмом.

Тому

dW_м= LIdI . (13.4.6)

Інтегруємо цей вираз у межах зміни енергії магнетного поля від 0 до W_м, а струму від 0 до І, одержимо

,

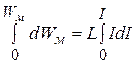або

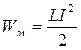. (13.4.7)

Вираз (13.4.7) визначає енергію магнетного поля котушки зі струмом.

Для довгого соленоїда L=mm₀n²V. Підставимо це значення L у (13.4.7), одержимо

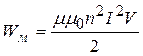. (13.4.8)

де m²m₀²n²І²=В² – квадрат індукції магнетного поля соленоїда.

З урахуванням цього зауваження одержуємо:

. (13.4.9)

При діленні енергії магнетного поля на об’єм одержимо об’ємну густину енергії магнетного поля, локалізованого в котушці

,

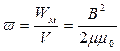або

. (13.4.10)

ЛЕКЦІЯ 14

МАГНЕТНЕ ПОЛЕ В РЕЧОВИНІ

14.1. Струми і механізм намагнечування. Намагнечуваність

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. IV. Закони ідеальних газів.
3. IV. Закономірності структурно-функціональної організації спинного мозку
4. А. Розрахунки з використанням дистанційного банкінгу.
5. Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
6. Автоматичне розвантаження по струму.
7. Аграрне право та законодавство США, Німеччини, Франції, Великої Британії, Ізраїлю, Польщі, Росії
8. Аграрні закони України
9. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
10. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
11. Адміністративна відповідальність за порушення аграрного законодавства
12. Адміністративна відповідальність за порушення земельного законодавства

Переглядів: 1502