• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Підстановки

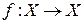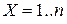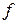Взаємно однозначна функція називається підстановкою на . Якщо множина|безліч| кінчена (), то можна вважати|лічити|, що . В цьому випадку підстановку зручно задавати таблицею з|із| двох рядків. У першому рядку – значення аргументів, в другій – відповідне значення функції. Нижче приведені приклади|зразки| довільних дискретних підстановок і :

, .

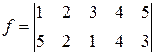Добичею|добутком| підстановок 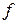і називається їх суперпозиція 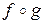. Суперпозиція – це результат послідовного застосування|вживання| двох підстановок. Твір|добуток| двох приведених вище підстановок рівний

.

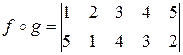Для обчислення|підрахунку| результату був використаний наступний|такий| алгоритм. Перший по номеру елемент підстановки 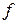рівний 5. Тому звертаємося|обертаємося| до п'ятого по номеру елементу підстановки і бачимо, що він також рівний 5. Означає|значить|, перший елемент твору|добутку| 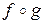буде рівний 5.

Другий елемент 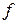рівний 2. Тому звертаємося|обертаємося| до другого елементу і бачимо, що він рівний 1. Останнє значення приймаємо як другого елементу добичі|добутку| 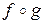. Діючи аналогічним чином, одержуємо|отримуємо| всі останні елементи добичі|добутку|.

Як можна бачити, добич|добуток| підстановок також є|з'являється,являється| підстановкою. Добич|добуток| підстановок визначена для підстановок однакового розміру. Добич|добуток| підстановок в загальному|спільному| випадку не володіє властивістю комутативності, тобто|цебто|

.

Одинична|поодинока| (або тотожна) підстановка – це підстановка 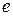така, що . Наприклад:

.

Зворотна підстановка по відношенню до підстановки 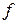– це підстановка, що задовольняє співвідношенню:

. (5.7)

Таблицю зворотної підстановки можна одержати|отримати|, якщо просто поміняти місцями рядки таблиці початкової|вихідної| підстановки. Наприклад:

, .

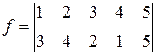Підстановки можна представляти|уявляти| в графічній формі, проводячи стрілки від кожного елементу 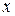до елементу .

Приклад|зразок| 5.6. Задана постановка

.

Графічне представлення цієї підстановки показане на мал. 5.2.

Мал. 5.2

У сучасній математиці операції, алгебри, застосовують не тільки|не лише| до скалярних чисел, але і до інших об'єктів. Наприклад, до матриць або підстановок. Безліч різних об'єктів, для яких визначені відповідні операції алгебри, називаються алгеброю в широкому сенсі|змісті,рації| цього слова. Якщо визначені чотири дії: складання, віднімання, множення і ділення|поділка,розподіл,поділ| – така алгебра називається полем.

Таким чином, звичайна|звична| алгебра (у вузькому сенсі|змісті,рації| цього слова) є|з'являється,являється| полем. Якщо операція ділення|поділки,розподілу,поділу| в алгебрі не визначена, така алгебра називається кільцем. Якщо визначена тільки|лише| одна операція, то алгебра називається групою. Причому, ця операція повинна володіти властивістю асоціативності:

,

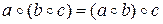сама алгебра повинна мати одиничний|поодинокий| елемент 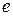з|із| властивістю:

,

і для кожного об'єкту мати зворотний елемент :

.

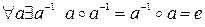Тепер ми можемо стверджувати, що безліч підстановок утворюють групу щодо|відносно| операції суперпозиції. Ця група називається симетричною ступеню|мірі| n.

Цикл – це послідовність елементів, така що

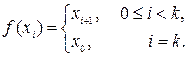
Цикл довжини 2 називається транспозицією.

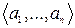Якщо прийняти угоду, що елементи верхнього рядка (аргументи) завжди розташовуються в певному порядку|ладі| (наприклад, за збільшенням), то верхній рядок можна не указувати|вказувати| – підстановка однозначно визначається нижнім рядком. Такі підстановки в один рядок називаються перестановками. Перестановку елементів позначатимемо |значитимемо|, де усі – різні числа з|із| діапазону .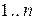

Якщо в перестановці для елементів і має місце нерівність при, то пара 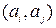називається інверсією. Позначимо 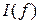– число інверсій в перестановці .

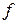Теорема 5.5. Довільну підстановку 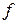можна представити|уявити| у вигляді суперпозиції 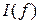транспозицій сусідніх елементів.

Доказ. Хай|нехай| 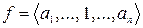. Переставимо 1 на перше місце, міняючи|змінюючи,замінюючи| її місцями з|із| сусідніми зліва|ліворуч| елементами. Позначимо послідовність цих транспозицій через . При цьому всі інверсії, в яких брала участь 1, пропадуть. Потім переставимо 2 на друге місце і т.д. Таким чином, 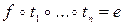і по властивості групи, причому .

Слідство|наслідок|. Всяке|усяке| сортування може бути виконане перестановкою сусідніх елементів.

Такий метод сортування відомий як бульбашковий метод. Цей метод простий, але|та| є|з'являється,являється| далеко не найефективнішим алгоритмом сортування.

Читайте також:

1. Метод підстановки

Переглядів: 3552