• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Лекція № 6. ЧИСЛА ФІБОНАЧЧІ І ПРОСТІ ЧИСЛА

6.1. Завдання|задача| Фібоначчі

Італійський математик Леонардо Фібоначчі жив в 13 сторіччі|столітті| і одним з перших в Європі став використовувати арабські (індійські) цифри. Він придумав|вигадав| дещо штучне завдання|задачу| про кроликів, яких вирощують на фермі, причому всі вони вважаються|лічаться| самками, самці ігноруються. Кролики починають|розпочинають,зачинають| розмножуватися після того, як їм виповнюється два місяці, а потім кожен місяць народжують по кролику. Кролики ніколи не вмирають|помирають,умирають|.

Потрібно визначити, скільки кроликів буде на фермі через n місяців, якщо в початковий момент часу був тільки|лише| один новонароджений кролик.

Очевидно, що фермер має одного кролика в перший місяць і одного кролика – в другий місяць. На третій місяць буде вже два кролики, на четвертий – три і т.д. Позначимо кількість кроликів в n місяці як 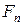. Таким чином: , , , , , …

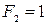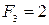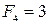Можна побудувати|спорудити| алгоритм, що дозволяє знайти при будь-якому n.

Згідно умові завдання|задачі| загальна|спільна| кількість кроликів 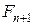в n+1 місяці розкладається на три складові:

· одномісячні кролики, не здібні до розмноження, в кількості

;

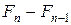· кролики, здібні до розмноження, в кількості ;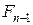

· новонароджені кролики, їх кількість також рівна .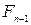

Таким чином, одержимо|отримаємо|

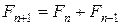. (6.1)

Формула (6.1) дозволяє обчислити|обчисляти,вичислити| ряд|лаву,низку| чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 , ...

Числа в даній послідовності називаються числами Фібоначчі.

Якщо прийняти і , то за допомогою формули (6.1) можна визначити всю решту чисел Фібоначчі. Формула (6.1) називається рекурентною формулою (recurrence – «повернення» на латині).

Перш ніж рухатися|сунутися| далі, розглянемо|розгледимо| наступне|таке| питання. Припустимо|передбачимо|, що є|наявний| сходи в n сходинок. Ми можемо підніматися|підійматися| по ній з|із| кроком в одну сходинку, або – з|із| кроком в дві сходинки. Скільки існує комбінацій різних способів підйому?

Якщо n = 1, є|наявний| тільки|лише| один варіант рішення задачі. Для n = 2 існує 2 варіанти: два одиничні|поодинокі| кроки або один подвійний. Для n = 3 існує 3 варіанти: три одиничні|поодинокі| кроки, або один одиничний|поодинокий| і один подвійний, або один подвійний і один одиничний|поодинокий|.

У наступному|такому| випадку n = 4, маємо 5 можливостей|спроможності| (1+1+1+1, 2+1+1, 1+2+1, 1+1+2, 2+2).

Для того, щоб відповісти на поставлене питання при довільному n, позначимо кількість варіантів як 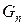, і спробуємо визначити 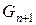по відомих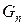і 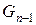. Якщо ми стартуємо з одиничного|поодинокого| кроку, то маємо 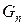комбінацій для n сходинок, що залишилися. Якщо стартуємо з подвійного кроку, то маємо 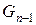комбінацій для тих, що залишилися n–1 сходинок. Загальна|спільна| кількість варіантів для n+1 сходинок рівно

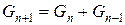. (6.2)

Одержана|отримана| формула як близнюк нагадує формулу (6.1). Проте|тим не менше|, це не дозволяє ототожнювати кількість комбінацій 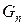з|із| числами Фібоначчі . Ми бачимо, наприклад, що 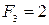, але|та| 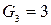. Проте|однак| має місце наступна|слідуюча| залежність:

.

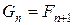Це справедливо для n = 1, 2, і також справедливо для кожного n. Числа Фібоначчі і кількість комбінацій 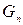обчислюються за однією і тією ж формулою, проте|однак| початкові значення, 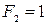і 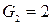у|в,біля| них розрізняються.

Читайте також:

1. Абсолютна величина числа позначається символом .
2. Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
3. Арифметичні операції над цілими числами
4. Бухгалтерські записи (проводки) – прості та складні.
5. Вид заняття: лекція
6. Вид заняття: лекція
7. Вид заняття: лекція
8. Вид заняття: лекція
9. Вид заняття: лекція
10. Визначення числа одиниць переносу
11. Визначення числа прокладок
12. Визначення. Числа й називаються комплексно спряженими.

Переглядів: 966