• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Арифметичні операції над цілими числами

У пам'яті комп'ютера операнди, як правило, зберігаються у прямому або додатковому кодах. Зберігати числа в оберненому коді недоцільно, тому що такий код

числа можна дуже легко отримати з прямого коду простою інверсією. Використання прямого коду числа дає переваги під час виконання деяких операцій (наприклад, множення) над операндами, що зображені у форматі з плаваючою комою. Ця обставина і є визначальним фактором при виборі способу збереження інформації у пам'яті комп'ютера.

При додаванні двох n-розрядних двійкових чисел (один біт знака та n-1 бітів значущих цифр) слід керуватися такими правилами.

1. Для того щоб додати два числа, необхідно додати їх n-бітове зображення, не враховуючи біт перенесення, який формується у старшому розряді. Сумою буде значення у додатковому коді, якщо результат належить діапазону від -2^n-1 до 2^n-1- 1.

2. Для віднімання числа Х від числа У необхідно спочатку обчислити додатковий код числа Y, а потім додати його до числа X, враховуючи перше правило. Результатом буде значення у додатковому коді, за умови, що воно належить діапазону від -2^n-1 до 2^n-1- 1.

При додаванні двох л-розрядних двійкових чисел (один біт знака та n-1 бітів значущих цифр) із використанням прямого та додаткового кодів можливий результат, кількість значущих цифр у якому дорівнюватиме n, тобто результат, що не належатиме діапазону допустимих значень. Таку ситуацію називають переповненням розрядної сітки. Ознакою переповнення є перенесення в знаковий розряд результату за відсутності перенесення зі знакового розряду (додатне переповнення) або наявність перенесення зі знакового розряду за відсутності перенесення в знаковий розряд (від'ємне переповнення). Якщо є перенесення як в знаковий розряд результату, так і зі знакового розряду або якщо ці перенесення відсутні, то переповнення не відбувається. При додатному переповненні результат операції від'ємний, при від'ємному - додатний.

Слід зазначити, що переповнення може виникнути лише при додаванні чисел з однаковими знаками. Додавання чисел із різними знаками не призводить до переповнення.

Приклад 1.9_______________________________________________________

Наведемо приклад додатного переповнення. В області пам'яті обсягом 1 байт зберігається число +65₁₀, прямим кодом якого є 0100 0001 (знаковий розряд містить 0). Якщо додати до цього числа таке саме, утвориться від'ємне число 1000 0010, оскільки відбудеться перенесення одиниці в знаковий розряд (знаковий біт результату міститиме 1). Десятковим еквівалентом числа, що утвориться, буде значення -2₁₀.

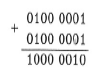
Далі наведемо приклад від'ємного переповнення. В області пам'яті обсягом 1 байт зберігається число -65₁₀, додатковий код якого - 1011 1111 (знаковий розряд містить 1). Якщо додати до цього числа таке саме, то утвориться додатне число 0111 1110, оскільки відбудеться перенесення одиниці зі знакового розряду (знаковий біт результату міститиме 0). Десятковим еквівалентом двійкового числа, що утвориться, буде число +126₁₀.

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

Виявити переповнення розрядної сітки буде простіше за умови використання модифікованого додаткового коду, коди для збереження знака числа відводиться не один, а два розряди. Щ розряди беруть участь в арифметичній операції нарівні з цифровими. За відсутності переповнення обидва знакові розряди містять однакові значення. Розбіжність у значеннях цих розрядів є ознакою того, що виникло переповнення.

Множення, порівняно з додаванням та відніманням, є більш складною операцією з точки зору як програмної, так і апаратної реалізації. У більшості комп'ютерів операція множення виконується як послідовність операцій додавання та зсуву. Для реалізації цієї операції у комп'ютерах застосовуються кілька різних алгоритмів, але кожен із них передбачає наявність в АЛП регістрів множника та множеного, а також спеціального регістру, який називається накопичувальним суматором. До початку операції множення цей регістр містить число 0. Під час операції у ньому зберігаються результати проміжних обчислень, a no завершенні - кінцевий результат.

Приклад 1.10_______________________________________________________

Приклад множення двох додатних чисел наведено нижче.

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

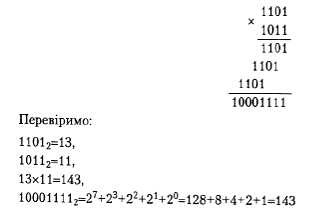
Ділення є дещо складнішою, ніж множення, операцією, але її реалізація в комп'ютері ґрунтується на тих самих принципах. Основою є загальновідомий спосіб ділення за допомогою операцій віднімання чи додавання та зсуву (ділення у стовпчик). Ділення виконується як послідовність віднімань дільника спочатку від діленого, а потім і від часткових залишків, які утворюються у процесі ділення. Ділене зазвичай займає 2и розрядів, тоді як дільник, частка та залишок є n-розрядними.

Читайте також:

1. Активні операції банків
2. Активні операції комерційних банків
3. Алгебраїчні операції
4. Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
5. Арифметичні оператори
6. Арифметичні операції
7. Арифметичні операції в різних системах числення
8. Арифметичні цикли. Оператор циклу For – Next
9. Банк і його операції. Правова природа банківської діяльності
10. Бартерні операції
11. Біржові операції.

Переглядів: 3763