• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рішення|розв'язання,вирішення,розв'язування|.

1. Дане відношення|ставлення| не є|з'являється,являється| симетричним, оскільки|тому що| матриця несиметрична. Наприклад, пара (2, 1) належить 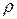, а пара (1, 2) йому не належить.

2. Відношення|ставлення| антисиметрично, оскільки|тому що| немає жодної пари , .

3. Відношення|ставлення| антисиметрично, але|та| не асиметрично, оскільки|тому що| на діагоналі матриці є|наявний| елементи, рівні 1.

4. Всі діагональні елементи матриці відношення|ставлення|, рефлексії, рівні 1. Дане відношення|ставлення| не є|з'являється,являється| рефлексією.

5. Відношення|ставлення| не володіє властивістю антирефлексивності, оскільки|тому що| діагональ матриці ненульова.

6. Дане відношення|ставлення| не є|з'являється,являється| транзитивним, оскільки|тому що|, наприклад, пари (1, 4) і (4, 3) належать 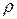, а пара (1, 3) йому не належить.

Знайдемо транзитивне замикання графа, заданого відношенням|ставленням| 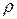. Процедура транзитивного замикання зводиться до додавання|добавки| в матрицю суміжності мінімального числа одиниць, так, щоб відповідне відношення|ставлення| володіло властивістю транзитивності. Для цього виконуємо наступні|такі| операції.

1. Обчислюємо|обчисляємо,вичисляємо| матрицю композиції . Для цього умножаємо|множимо| (з використанням операції логічного множення) матрицю A саму на себе: 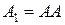. Така добич|добуток| називається добичею|добутком| булевих матриць. Результат добичі|добутку| одержують|отримують| таким чином. Елемент результуючої матриці, якщо хоч би в одному випадку k-й| елемент i-йрядки першого співмножника і k-й| елемент j-гостовпця другого співмножника одночасно рівні одиниці. Інакше .

.

2. Знаходимо|находимо| логічну суму (диз'юнкцію) матриць. Поелементна диз'юнкція матриць дає:

.

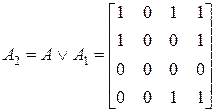3. Порівнюємо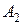з|із| A. Якщо 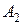= A, то 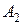– шукана матриця. Якщо , то вважаємо |гадаємо|, повертаємося до п. 1 і повторюємо всю процедуру для нової матриці. В даному випадку . Тому приймаємо:

.

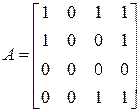Умножаємо|множимо| матрицю саму на себе:

.

Знаходимо|находимо| логічну суму:

.

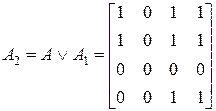Порівнюємо: . Вважаємо|гадаємо| і повторюємо процедуру ще раз.

.

.

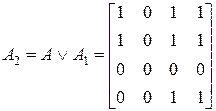Порівнюємо: 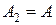. Отже, 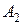– матриця транзитивного замикання заданого відношення|ставлення|.

На мал. 13.2 (а і б) представлені|уявлені| графи відношення|ставлення| 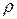і його транзитивного замикання. Діагональні елементи матриці відповідають петлям на графі. Матриця несиметрична, тому граф відношення|ставлення| – орієнтований.

Мал. 13.2

Переглядів: 927