
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
THE IDEA OF UNIFICATION
Having in essence the same initial idea of phrase structures and their context-free combining, the HPSG and several other new approaches within Chomskian mainstream select the general and very powerful mathematical conception of unification. The purpose of unification is to make easier the syntactic analysis of natural languages.
The unification algorithms are not linguistic proper. Rather they detect similarities between parts of mathematical structures (strings, trees, graphs, logical formulas) labeled with feature sets. A priori, it is known that some features are interrelated, i.e., they can be equal, or one of them covers the other. Thus, some feature combinations are considered compatible while met in analysis, whereas the rest are not. Two sets of features can be unified, if they are compatible. Then the information at an object admitting unification (i.e., at a constituent within a sentence to be parsed) combines the information brought by both sets of features.
Unification allows filtering out inappropriate feature options, while the unified feature combination characterizes the syntactic structure under analysis more precisely, leading to the true interpretation of the sentence.
As the first example of unification operations, let us compare feature sets of two Spanish words, el and muchacho, staying in a text side by side. Both words have the feature set [gender = masculine, number = singular], so that they are equivalent with respect to gender and number. Hence, the condition of unification is satisfied, and this pair of words can form a unifying constituent in syntactic analysis.
Another example is the adjacent Spanish words las estudiantes. The article las has the feature set [gender = feminine, number = plural]. As to the string estudiantes, this word can refer to both ‘he-student’ of masculine gender and ‘she-student’ of feminine gender, so that this word is not specified (is underspecified) with respect to gender. Thus, the word occurrence estudiantes taken separately has a broader feature set, namely, [number = plural], without any explicit indication of gender. Since these two feature sets are not contradictory, they are compatible and their unification [gender = feminine, number = plural] gives the unifying constraint set assigned to both words. Hence, this pair can form a unifying mother constituent las estudiantes, which inherits the feature set from the head daughter estudiantes. The gender of the particular word occurrence estudiantes is feminine, i.e., ‘she-students,’ and consequently the inherited gender of the noun phrase las estudiantes is also feminine.
As the third example, let us consider the words niño and quisiera in the Spanish sentence El niño quisiera pasar de año. The noun niño is labeled with the 3rd person value: [person = 3], whereas the verb quisiera exists in two variants labeled with the feature set [person = 1 or person = 3], correspondingly. Only the latter variant of the verb can be unified with the word niño. Therefore this particular word occurrence of quisiera is of the third person. The whole sentence inherits this value, since the verb is its head daughter.
THE MEANING Û TEXT THEORY:
MULTISTAGE TRANSFORMER AND GOVERNMENT PATTERNS
The European linguists went their own way, sometimes pointing out some oversimplifications and inadequacies of the early Chomskian linguistics.
In late 1960´s, a new theory, the Meaning Û Text model of natural languages, was suggested in Russia. For more than 30 years, this theory has been developed by the scientific teams headed by I. Mel’čuk, in Russia and then in Canada, and by the team headed by Yu. Apresian in Russia, as well as by other researchers in various countries. In the framework of the Meaning Û Text Theory (MTT), deep and consistent descriptions of several languages of different families, Russian, French, English and German among them, were constructed and introduced to computational practice.
One very important feature of the MTT is considering the language as multistage, or multilevel, transformer of meaning to text and vice versa. The transformations are comprehended in a different way from the theory by Chomsky. Some inner representation corresponds to each level, and each representation is equivalent to representations of other levels. Namely, surface morphologic, deep morphologic, surface syntactic, deep syntactic, and semantic levels, as well as the corresponding representations, were introduced into the model.
The description of valencies for words of any part of speech and of correspondence between the semantic and syntactic valencies have found their adequate solution in this theory, in terms of the so-called government patterns.
The government patterns were introduced not only for verbs, but also for other parts of speech. For a verb, GP has the shape of a table of all its possible valency representations. The table is preceded by the formula of the semantic interpretation of the situation reflected by the verb with all its valencies. The table is succeeded by information of word order of the verb and its actants.
If to ignore complexities implied by Spanish pronominal clitics like me, te, se, nos, etc., the government pattern of the Spanish verb dar can be represented as
Person X gives thing Y to person Z
| X = 1 | Y = 2 | Z = 3 |
| 1.1 N | 2.1 N | 3.1 aN |
The symbols X, Y, and Z designate semantic valencies, while 1, 2, and 3 designate the syntactic valencies of the verb. Meaning ‘give’ in the semantic formula is considered just corresponding to the Spanish verb dar, since dar supposedly cannot be represented by the more simple semantic elements.
The upper line of the table settles correspondences between semantic and syntactic valencies. For this verb, the correspondence is quite simple, but it is not so in general case.
The lower part of the table enumerates all possible options of representation for each syntactic valency at the syntactic level. The options operate with part-of-speech labels (N for a noun, Vinf for a verb in infinitive, etc.) and prepositions connecting the verb with given valency fillers. In our simplistic example, only nouns can fill all three valencies, only the preposition a is used, and each valency have the unique representation. However, such options can be multiple for other verbs in Spanish and various other languages. For example, the English verb give has two possible syntactic options for the third valency: without preposition (John gives him a book)vs. with the preposition to (John gives a book to him).
The word order is generally not related with the numeration of the syntactic valencies in a government pattern. If all permutations of valencies of a specific verb are permitted in the language, then no information about word order is needed in this GP. Elsewhere, information about forbidden or permitted combinations is given explicitly, to make easier the syntactic analysis. For example, the English verb give permits only two word orders mentioned above.
Thus, government patterns are all-sufficient for language description and significantly differ from subcategorization frames introduced in the generative grammar mainstream.
THE MEANING Û TEXT THEORY: DEPENDENCY TREES
Another important feature of the MTT is the use of its dependency trees, for description of syntactic links between words in a sentence. Just the set of these links forms the representation of a sentence at the syntactic level within this approach.
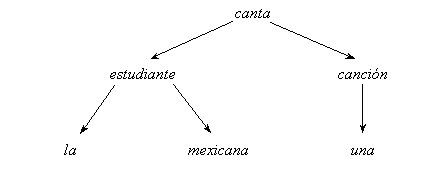 FIGURE II.2. Example of a dependency tree.
FIGURE II.2. Example of a dependency tree.
|
For example, the Spanish sentence La estudiante mexicana canta una canción can be represented by the dependency tree shown in Figure II.2. One can see that the dependency tree significantly differs from the constituency treefor the same sentence (cf. Figure II.1).
Up to the present, the proper description of the word order and word agreement in many languages including Spanish can be accomplished easier by means of the MTT. Moreover, it was shown that in many languages there exist disrupt and non-projective constructions, which cannot be represented through constituency trees or nested structures, but dependency trees can represent them easily.
In fact, dependency trees appeared as an object of linguistic research in the works of Lucien Tesnière, in 1950’s. Even earlier, dependencies between words were informally used in descriptions of various languages, including Spanish. However, just the MTT has given strict definition to dependency trees. The dependency links were classified for surface and deep syntactic levels separately. They were also theoretically isolated from links of morphologic inter-word agreement so important for Spanish.
With dependency trees, descriptions of the relationships between the words constituting a sentence and of the order of these words in the sentence were separated from each other. Thus, the links between words and the order in which they appear in a sentence were proposed to be investigated apart, and relevant problems of both analysis and synthesis are solved now separately.
Hence, the MTT in its syntactic aspect can be called dependency approach, as contrasted to the constituency approach overviewed above. In the dependency approach, there is no problem for representing the structure of English interrogative sentences (cf. page 39). Thus, there is no necessity in the transformations of Chomskian type.
To barely characterize the MTT as a kind of dependency approach is to extremely simplify the whole picture. Nevertheless, this book presents the information permitting to conceive other aspects of the MTT.
THE MEANING Û TEXT THEORY: SEMANTIC LINKS
The dependency approach is not exclusively syntactic. The links between wordforms at the surface syntactic level determine links between corresponding labeled nodes at the deep syntactic level, and after some deletions, insertions, and inversions imply links in the semantic representation of the same sentence or a set of sentences. Hence, this approach facilitates the transfer from syntactic representations to a semantic one and vice versa.
According to the MTT, the correlation between syntactic and semantic links is not always straightforward. For example, some auxiliary words in a sentence (e.g., auxiliary verbs and some prepositions) are treated as surface elements and disappear at the deep syntactic level. For example, the auxiliary Spanish verbHABER in the word combination han pedido disappears from the semantic representation after having been used to determine the verb tense and mode. At the same time, some elements absent in the surface representation are deduced, or restored, from the context and thus appear explicitly at the deep syntactic level. For example, given the surface syntactic dependency tree fragment:
su hijo ® Juan,
the semantically conditioned element NAME is inserted at the deep syntactic level, directly ruling the personal name:
su hijo ® NAME ® Juan
Special rules of inter-level correspondence facilitate the transition to the correct semantic representation of the same fragment.
The MTT provides also the rules of transformation of some words and word combinations to other words and combinations, with the full preservation of the meaning. For example, the Spanish sentence Juan me prestó ayudacan be formally transformed to Juan me ayudó and vice versa at the deep syntactic level. Such transformations are independent of those possible on the semantic level, where mathematical logic additionally gives quite other rules of meaning-preserving operations.
We should clarify that some terms, e.g., deep structure or transformation, are by accident used in both the generative and the MTT tradition, but in completely different meanings. Later we will return to this source of confusion.
All these features will be explained in detail later. Now it is important for us only to claim that the MTT has been able to describe any natural language and any linguistic level in it.
Читайте також:
- Economic and Political Unification. Conditions for Linguistic Unity
- The unification of the ways of building the plural forms of nouns in the history of English
| <== попередня сторінка | | | наступна сторінка ==> |
| HEAD-DRIVEN PHRASE STRUCTURE GRAMMAR | | | CONCLUSIONS |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |