Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Зв'язок між описом системи у просторі станів та передавальною фкунцією

Якщо динаміка системи задана рівняннями стану, то для визначення передаточних функцій систем необхідно на першому етапі знайти перетворення Лапласу від лівої та правої частин цих рівнянь

, (1.28)

де s – комплексна змінна;

x(s), u(s), y(s) – перетворення Лапласа відповідних векторів та змінних;

γ(s) – перетворення Лапласа вектору збурень;

x(0) – вектор початкових значень стану системи або об’єкта.

Розв’язок першого рівняння з системи (1.28) відносно x(s) дозволяє записати, що

, (1.29)

де E_n – одинична матриця розміру n×n. Підстановка результату (1.29) до другого рівняння системи (1.28) дозволяє визначити зображення за Лапласом вектору вихідних сигналів системи як

. (1.30)

З виразу (1.30) видно, що система однаково реагує на зміну початкових умов та збурень стану, тому динаміка системи може бути визначена з допомогою двох матриць передаточних функцій. Перша – передаточна функція системи за входом u

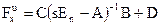. (1.31)

Друга – матриця передаточних функцій за збуренням γ

. (1.32)

Для побудови структурної схеми системи у просторі станів визначимо чому дорівнює передаточна функція багатовимірної системи із зворотним зв’язком, рис. 1.6. Як відомо[Блохін] передатна функція системи W(s) зв’язує зображення Лапласа вихідного сигналу ДС x(s) із зображенням вхідного u(s)

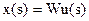. (1.32)

Рис. 1.6 Структурна схема системи із зворотнім зв’язком

Отже, виходячи із структури на рис. 1.6, можна записати, що

Виключення з наведених рівнянь допоміжних векторів z(s) та h(s) дозволяє знайти зв’язок між векторами x(s) та u(s) у вигляді

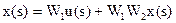. (1.33)

Оскільки вектор x(s) має η компонентів, то рівняння (1.33) в результаті розділення змінних переписується у вигляді

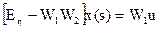; (1.34)

де E_η – одинична матриця розміру η×η. Розв’язок рівняння (1.34) відносно вектора x(s) дозволяє визначити, що

; (1.35)

або в разі квадратної матриці W₁

. (1.36)

Порівняння виразів (1.32), (1.35) та (1.36) дозволяє визначити передатну функцію системи із зворотнім зв’язком у вигляді

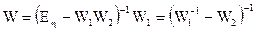. (1.37)

Розгляд рівнянь (1.31), (1.32) та (1.37) дозволяє записати наступне співвідношення

, (1.38)

звідки слідує, що різницю (sE_n-A)^-1 на структурній схемі можна замінити з’єднанням двох багатовимірних елементів з передатними функціями

;

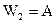
за схемою з рис. 1.6.

Таким чином, структурна схема ДС з оператором типу (1.7) легко приводиться до вигляду представленому на рис. 3.2.

Рис. 1.7 Структурна схема системи у просторі станів

Приклад.Припустимо динаміка системи задана рівняннями стану такими, що

; ; ; .

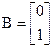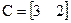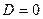Необхідно знайти передавальну функцію системи.

<== попередня сторінка	\|	наступна сторінка ==>
Оператори одновимірної динамічної системи	\|	Розв’язок

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.