• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Оператори одновимірної динамічної системи

Якщо ДС має скалярні вхідні r, u, ψ та вихідні x сигнали, то таку систему називають одновимірною. Для зображення її структури подвійні лінії замінюють на одинарні. На вході та виході оператора такої системи діють скалярні сигнали. В таких умовах в якості операторів даних ДС найбільш поширено використання передатної функції, звичайного диференціального рівняння або рівнянь стану. Для лінійних стаціонарних ДС при нульових початкових умовах в якості оператора А_і можна визначити передатну функцію. В загальному вигляді, як відомо з ТАУ [1] , передатна функція представляється як

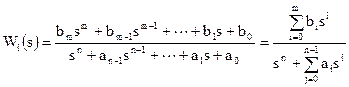, (1.4)

де а_і, b_i – параметри оператора (передатної функції); s – незалежна комплексна змінна; n, m – порядки поліномів знаменника та чисельника.

При визначенні оператора системи у вигляді звичайного диференціального рівняння її динаміка характеризується виразом [1]

(1.5)

або

(1.6)

де x – вихідний сигнал оператора, u – вхідний сигнал.

В залежності від співвідношення між порядками оператора ДС поділяють на строго правильні та правильні. Якщо n>m, то ДС називають строго правильною. В разі коли n≥m, систему називають правильною. Визначення оператора системи у просторі станів можливе лише, коли вона належить до правильної або строго правильної ДС.

Оператор визначений у просторі станів виглядає як наступна система диференціальних рівнянь першого порядку [Тунік]

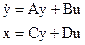, (1.7)

де y – n-вимірний вектор стану ДС

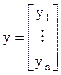; (1.8)

крапка над вектором позначає взяття першої похідної за часом; А – числова матриця стану ДС (матриця Фробеніуса), яка має розмірність n×n та дорівнює

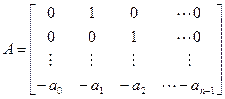; (1.9)

В – матриця управління, яка в разі скалярної системи має n рядків та один стовпчик і дорівнює

; (1.10)

С - матриця спостереження, яка має один рядок та n стовпчиків. Її вигляд залежить від співвідношення між порядками n та m

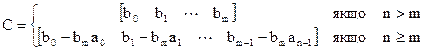; (1.11)

D – коефіцієнт (матриця) прямої передачі управління, вигляд якого також залежить від співвідношення між порядками поліномів чисельника та знаменника передатної функції

. (1.12)

Порівняння отриманих залежностей вказує на можливість переходу від однієї форми запису оператора до іншої.

Приклад 1.1.

Задано оператор скалярної системи у вигляді передаточної функції W такої, що

.

Необхідно знайти звичайне диференціальне рівняння та систему рівнянь стану.

Для розв’язання задачі спочатку необхідно знайти порядки поліномів чисельника та знаменника. Вони дорівнюють m=1, n=2. Після цього знайти параметри оператора b₀=3, b₁=2, a₀=5, a₁=3. За знайденими значеннями параметрів та на основі рівняння (1.5) визначимо звичайне диференціальне рівняння

.

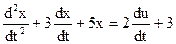Для складання рівнянь стану введемо вектор станів y. Оскільки порядок поліному знаменника n=2, то цей вектор має вигляд

.

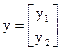Матриця станів А з урахуванням правила (1.9) представляється як

.

Оскільки m=1, то матриця керування B дорівнює

.

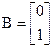Матриця спостереження C може бути визначена за відомими параметрами на основі правила (1.11). Отже, оскільки система строго правильна, то

,

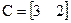а коефіцієнт прямої передачі керування дорівнює нулю.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. POS-системи
8. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
9. VI. Філогенез нервової системи
10. А) Заробітна плата її форми та системи.
11. А) Заробітна плата, її форми та системи.
12. А) Поліпшення системи зворотного зв'язку.

Переглядів: 630