• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

V.Коливання та хвилі

45. Гармонічні коливання.

Диференціальне рівняння гармонічних коливань

Коливанням називається будь-який рух або зміна стану тіла, що характеризуєть­ся тим чи іншим ступенем повторюванос­ті в часі значень фізичних величин, які визначають цей рух або стан тіла.

Коливання називаютьсявільними, якщо вони здійснюються за рахунок енергії, яка була надана спочатку, за відсутності в наступному зовнішніх впливів на коливну систему.

Коливання називаютьсяперіодични­ми, якщо значення фізичних величин, які змінюються під час коливань, повторю­ються через однакові проміжки часу. Найпростішим типом періодичних коливань є так звані гармонічні коливання – коливання, при яких значення фізичної величини зміню­ється з часом за законом косинуса (синуса).

Нехай матеріальна точка здійснює прямолінійні гармонічні коливання вздовж осі координат ОХ біля положення рівноваги, яке прийняте за початок координат. Тоді залежність координати x від часу t задається рівнянням

.

Тут х – зміщення коливної точки; А – ам­плітуда коливання ( 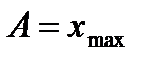); 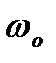– цик­лічна частота; 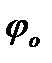– початкова фаза коли­вань в момент часу t=0 ; 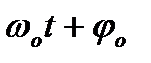– фаза коливань в момент часу t.

Найменший проміжок часу T, після проходження якого повторюються значення всіх фізичних величин, що характеризують коливання, називаєтьсяперіодом коливання. За час T здійснюється одне повне коливання і фаза коливань отримує приріст 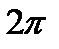, тобто

.

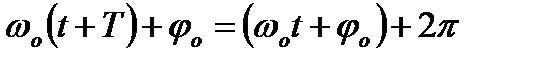Звідси

.

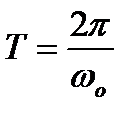Частотою коливань називається кількість повних коливань, що здійснюють­ся за одиницю часу:

.

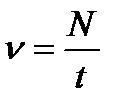де N – кількість коливань, виконаних за час t. Частота коливань - величина, яка обернена до періоду коливань:

.

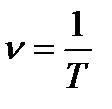Циклічна частота .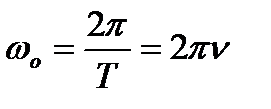

Отже, циклічна частота дорівнює кількості повних коливань, що здійснюється за 2 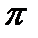с.

Коливний процес характеризується швидкістю і прискоренням коливної точки:

;

,

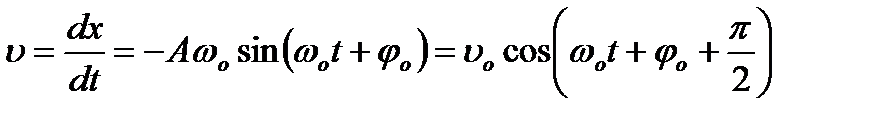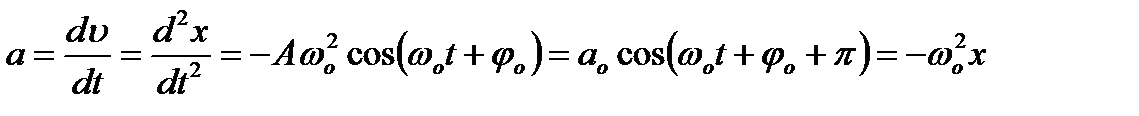де – амплітуда швидкості, а – амплітуда прискорення. Зміщен­ня, швидкість і прискорення точки, що гармонічно коливається, є періодичними функціями часу з однаковими циклічною частотою 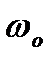періодом Т. Фаза швидкості відрізняється від фази зміщення на , а фаза прискорення відрізняється від фази зміщення на .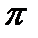

Прискорення завжди напрямлене до положення рівноваги: віддаляючись від по­ложення рівноваги, коливна точка рухаєть­ся сповільнено, наближаючись до нього прискорено. Прискорення прямо пропор­ційне до зміщення, а його напрямок проти­лежний до напрямку зміщення.

Другий закон закон Ньютона дає змогу в загальному вигляді записати зв’язок між силою і прискоренням для прямоліній­них гармонічних коливань матеріальної точки з масою m:

.

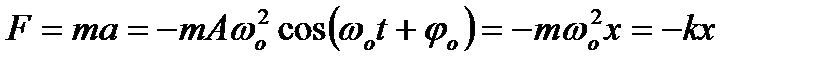Сила, що діє на коливну матеріальну точку прямо пропорційна до зміщення і зав­жди напрямлена до положення рівноваги. То­му її називають повертальною силою. Фаза сили F збігається з фазою прискорення.

Прикладом сил, що задовольняють співвідношення 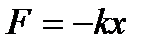є пружні сили. Сили F, що мають іншу природу, ніж пружні сили, але також задовольняють умо­ву 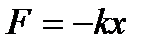, називаються квазіпружними, а 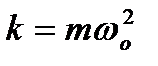– коефіцієнтом квазіпружної сили. Для прямолінійних коливань вздовж осі ОХ прискорення .

Тоді , , , .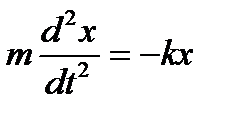

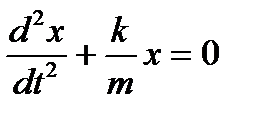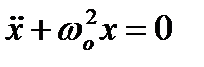Це диференціальне рівняння вільних прямолінійних гармонічних коливань, збуджених пружними або квазіпружними силами.

Частковими розв’язками цього дифе­ренціального рівняння є функції:

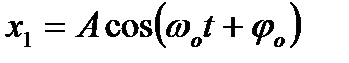i .

Кінетична енергія матеріальної точки, що здійснює гармонічні коливання, дорівнює:

.

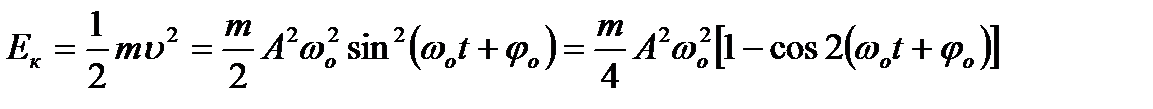Потенціальна енергія матеріальної точки, що здійснює гармонічні коливання під дією квазіпружної сили, дорівнює:

.

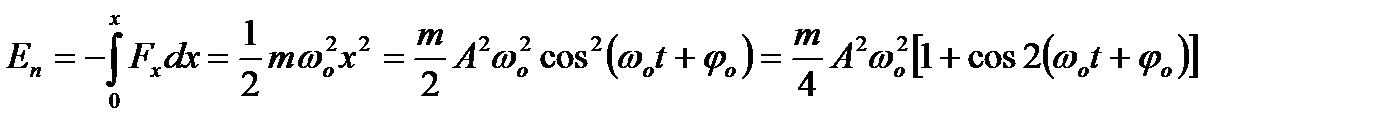Повна мехачічна енергія коливної точки:

.

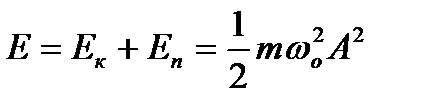Читайте також:

1. Визначення довжини хвилі
2. Визначення параметрів хвилі прориву
3. Гармонічний коливний рух і хвилі
4. Довжина світлової хвилі в середовищі
5. Довжиною хвилі є відстань, на яку поширюється хвильовий процес за час одного періоду коливань.
6. Експериментальна довжину хвилі де Бройля для кульки та електрона, що рухаються?
7. ЕЛЕКТРОМАГНІТНІ ХВИЛІ
8. Електромагнітні хвилі
9. Електромагнітні хвилі РНЧ-діапазону
10. Електромагнітні хвилі. Шкала електромагнітних хвиль
11. ЕНЕРГІЯ ЕЛЕКТРОМАГНІТНОЇ ХВИЛІ

Переглядів: 2844