Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ТЕМА 12.

КОМПЛЕКТУВАННЯ МАШИН ПО ОБ´ЄКТАМ УДІВНИЦТВА

Завантаження машин або задача лінійного

програмування про призначення

При вирішенні задач комплексні механізації будівництва інколи доводиться вводити такі змінні X_ij, які можуть "приймати тільки два значення: «1» або «0» "

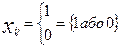
Причому ,якщо X_ij =1 , то вважається що даний комплект машин призначається на певний об´єкт.

Якщо X_ij =0 , то даний комплект не призначається на певний об'єкт. Звичайно в задачах на призначення i=j=n , тобто число комплектів машин дорівнює числу видів робіт , що виконується , тому число невідомих у таких задачах дорівнює n² . Але важливо те, що , тільки nіз них дорівнює «1», а інші n дорівнюють «0» так як кожний комплект машин призначається тільки на один вид робіт (об'єкт) , то повинна виконуватися умова :

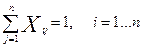. (1)

Умовою того ,що на об'єкті працює тільки один комплект є сума :

. (2)

Критерій оптимізації виражається у вигляді суми добутків:

. (3)

де C_ij – затрати часу на монтаж по об'єктах або продуктивність машин на об'єктах.

Умовою оптимізації є Y_min або Y_max в залежності від вибраного критерію оптимальності.

Умови (1) і (2) є математичною моделлю задачі про призначення.

Змістовна постановка задачі

Для монтажу трьох об'єктів є три крани (n=3). Із звітних даних відомо час на монтаж по об'єктах. Потрібно так розподілити крани по об'єктах , щоб сумарний час на їх монтаж був мінімальним

Вихідні дані зводимо в таблицю.

B_j A_i	B₁	B₂	B₃	d_i
	C₁₁= 3	C₁₂= 7	C₁₃= 5
	C₂₁= 2	C₂₂= 4	C₂₃= 4
	C₃₁= 4	C₃₂= 7	C₃₃= 2
b_j

A_j- кран під номером i;

B_j – об'єкт під номером j;

a_i – число об'єктів , яке приходиться на i-ту машину;

b_j – число машин , призначених на об'єкт з номером j;

C_ij – затрати часу на монтаж об'єктів.

Встановлення взаємо зв'язків та побудування математичні моделі

Введемо змінні ,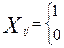

де 1- якщо кран призначається на об'єкт;

0 – якщо кран не призначається на цей об'єкт.

Сумуючи по об'єктах, отримаємо :

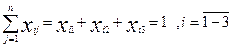
Аналогічно по стовпцях :

Сумарний час на монтаж трьох об'єктів трьома кранами :

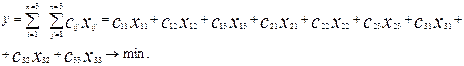
Таким чином поставлена задача звелася до знаходження 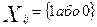, при яких задовольняються шість обмежень рівностей і досягається мінімум цільової функції (Y_min).

Дослідження математичної моделі

У випадку використання наскрізної нумерації змінних і затрат часу вихідну інформацію (табл.) можна записати у вигляді L₀_,

Перший рядок відповідає обмеженню з номером і=1.

Розв'язання зводиться до отримання трьох правильних стовпців у різних рядках. При цьому призначення будуть повними, тобто n=3, а рішення оптимальним.

Щоб скоротити перетворення і розрахунок тут доцільно скласти таблицю із вказівкою номерів рядків і номерів стовпців.

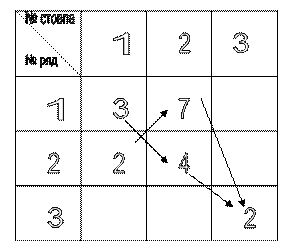
Задача вирішується на мінімум

У_min=С

У_{min=3∙1+4∙1+2∙1=9}

Х₁=Х₁₁=1

Х_з=Х₂₂=1

Х₄=Х₃₃=1

Х₁=Х₁₁=1

Х₃=Х₂₂=1

Х₉=Х₃₃=1

<== попередня сторінка	\|	наступна сторінка ==>
ВИЗНАЧЕННЯ ОБЛАСТІ ОПТИМАЛЬНОГО ВИКОРИСТАННЯ КОМПЛЕКТІВ МАШИНИ	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.