Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Тема 12

Планування імітаційних експериментів у процесі дослідження та оптимізації систем

План

1. Планування імітаційних експериментів у процесі дослідження систем.

2. Планування імітаційних експериментів у процесі оптимізації систем.

3. Оптимізація систем за методом Бокса – Уїлсона.

Література:[ 3, 5, 6].

Планування імітаційних експериментів у процесі дослідження систем

При експериментальному дослідженні систем ставиться задача вивчити вплив факторів системи на вихідну величину, яка описує функцію відгуку, адекватно описуючи поводження системи в заданій області факторного простору. Залежність дає змогу виявити вплив на функцію відгуку не лише кожного з факторів, а також і будь-якої їх комбінації.

Коефіцієнти при незалежних змінних відбивають рівень впливу факторів. Якщо коефіцієнт додатній, то зі збільшенням фактора зростає вихідний параметр системи. При від'ємному коефіцієнті зростання відповідного фактора спричинюється до зменшення величини . Коефіцієнти при лінійних членах відповідають вкладу даного фактора у величину параметра системи у при переході фактора з нульового рівня на верхній чи нижній. Головним ефектомфактора називають його внесок при переході від нижнього рівня до верхнього. Головний ефект у кодованій системі вимірювання факторів дорівнює подвоєному коефіцієнту при відповідній змінній .

Для оцінювання головних ефектів можна використовувати неповні (дробові) факторні плани. Проте для нелінійних моделей оцінювати ефекти факторів при дробових планах непросто, оскільки відбувається змішування ефектів.Наприклад, головний ефект може бути змішаний з однією чи кількома взаємодіями вищого порядку, що ускладнює вирізнення головного ефекту серед комбінації з іншими ефектами.

Як уже зазначалося, рівняння регресії наближено відповідає ряду Тейлора, побудованого для функції відгуку, а коефіцієнти 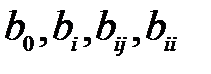є статистичними оцінками коефіцієнтів ряду Тейлора 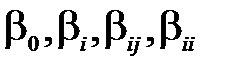. Проте ці оцінки бувають незалежними не для всіх планів, тобто не завжди оцінюють лише один відповідний коефіцієнт ряду Тейлора. Спостерігається явище змішування статистичних оцінок. Оцінки найменше змішуються в повних факторних планах. У квадратичних рівняннях регресії оцінки головних ефектів та ефектів взаємодії факторів не змішуються:

(10.1)

(10.2)

У задачах дослідження системи повні факторні плани дають змогу найточніше вивчити механізм впливу факторів на досліджувану систему і, як наслідок, сформулювати найбільш обгрунтовані висновки.

Проте в багатофакторних системах здійснення повних факторних експериментів пов'язане зі значними труднощами. Насамперед ідеться про необхідність проведення великого числа спроб у точках факторного простору, які до того ж мають багаторазово дублюватися. Тому за таких умов часто застосовуються дробові факторні плани, для яких значною мірою характерне змішування статистичних оцінок.

Планування імітаційних експериментів у процесі оптимізації систем

Проведення експериментів (натурних чи імітаційних) для пошуку оптимальних рішень полягає в реалізації деякої обчислювальної схеми знаходження екстремумів невідомої функції відгуку на заданій множині точок факторного простору. Нині розроблено численні наближені методи оптимізації, проте ефективність кожного з них істотно залежить від вигляду функції відгуку.

Головна складність постановки експериментів для оптимізації систем полягає в тому, що експериментатор не має відомостей про властивості функції відгуку. Отже, після закінчення експерименту, який реалізує деяку схему пошуку екстремуму, не може бути цілковитої впевненості в тому, що здобутий розв'язок є оптимальним. Під час виконання особливо відповідальних розрахунків для підвищення надійності результатів доцільно використовувати комбінації різних методів оптимізації.

Нагромаджений досвід розв'язування нелінійних оптимізаційних економіко — математичних задач у теорії керування запасами та календарному плануванні дає змогу зробити деякі узагальнені висновки щодо властивостей функцій відгуку, що відображують оптимізаційний процес в економіко-виробничих системах.

У загальному випадку функція відгуку (цільова функція) є багатоекстремальною, тобто має багато локальних екстремумів, серед яких може бути й кілька абсолютних. З огляду на це потрібно обережно використовувати методи напрямленого (детермінованого чи випадкового) пошуку екстремуму.

Друга важлива властивість оптимізаційних економіко — математичних моделей полягає в тому, що в області екстремумів функція відгуку є "'гладкою", тобто варіювання змінних у цій області не спричиняється до помітних змін значень цільової функції. Це полегшує пошуки оптимальних розв'язків, оскільки за умов неточної вхідної інформації (чим характерні економічні задачі) для практичних цілей досить дістати результат, близький до оптимального.

Принципово можливі два способи знаходження екстремуму фунукції відгуку:

(10.3)

Перший полягає в тому, що за допомогою експериментальних досліджень визначається математична модель функції відгуку, яка потім досліджується на екстремум класичними методами диференціального числення. З цією метою обчислюються частинні похідні функції відгуку і відшукуються стаціонарні точки розв’язування системи рівнянь
Розв'язок системиможе бути точкою оптимуму функції відгуку. У цьому переконуються або з допомогою формальних методів, або на підставі інтуїтивних міркувань.

Важливим моментом в описаному способі оптимізації є знаходження частинних похідних функції відгуку і обчислення точок, в яких похідні набувають нульових значень. Похідні функції відгуку можна визначити і без використання її математичної моделі. Для цього з допомогою повного чи дробового факторного плану досить знайти коефіцієнти лінійної регресії, що є статистичними оцінками коефіцієнтів ряду Тейлора:

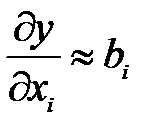( (10.4)

3. Оптимізація систем за методом Бокса–Уїлсона

Задача пошуку екстремуму функції відгуку (параметра оптимізації) зводиться до визначення точок в яких коефіцієнти лінійної регресії дорівнюють нулю. На цій умові базується другий спосіб оптимізації систем, запропонований Боксом та Уїлсоном (1951 р). Тому описаний далі метод має назву метод Бокса – Уїлсона.У спеціальній літературі він відомий і як метод крутого сходження (при визначенні точки максимуму).

Розглянемо загальну схему методу.

Спочатку вибирається точка (одна або кілька) факторного простору, яка за інтуїтивними міркуваннями може міститися поблизу точок екстремуму. Якщо немає жодних додаткових відомостей на користь пріоритету “екстремальності” деяких точок факторного простору, то початкова точка вибирається за методом Монте-Карло: значення рівнів факторів рівномірно і випадково генеруються в заданих межах їх змінювання.

В околі початкової точки за описаними правилами ставиться повний чи дробовий факторний експеримент. Потім проводиться статистичне дослідження здобутої лінійної регресії щодо перевірки однорідності дисперсій, значущості коефіцієнтів регресії, адекватності моделі. Фактично в околі початкової точки функція відгуку замінюється деякою гіперплощиною, коефіцієнти при лінійних членах якої є коефіцієнтами регресії:

(10.5)

Якщо початкова точка не є підозрілою на екстремум, тобто не всі коефіцієнти статистично незначущі, то коефіцієнти регресії використовуються для визначення напряму руху до стаціонарної точки (надалі для визначеності розглядатимемо лише випадок максимізації функції відгуку). Круте сходження до точки максимуму відбувається за напрямом градієнта, який визначає напрям найшвидшого зростання функції:

, (10.6)

де — одиничні вектори в напрямі координатних осей, що відповідають факторам .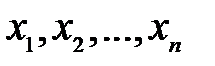

Вихідною точкою руху в напрямі крутого сходження є початкова точка в околі якої здобуто апроксимуючу гіперплощину. У вибраному напрямі в кількох точках факторного простору обчислюються значення функції відгуку, тобто в них провадяться експериментальні (імітаційні) спроби для визначення функції відгуку.

Експериментальне відшукання значень функції відгуку в напрямі крутого сходження триває доти, доки не трапиться точка, в якій значення функції відгуку буде більшим, ніж у решті точок (включаючи точки з вищими індексами). Знайдена точка використовується як нова початкова точка планування експерименту.

Після кількох ітерацій дістаємо точку, в якій усі коефіцієнти лінійної регресії будуть статистично незначущі, тобто bi 0 . Це означає, що локальна гіперплощина майже горизонтальна і не дає змоги вибрати наступний напрям руху до максимуму. Дана точка є підозрілою точкою щодо екстремуму, тобто вона може бути точкою локального максимуму.

Для прийняття остаточного рішення необхідно ретельно дослідити функцію відгуку в підозрілій точці.

Оскільки досліджувана поверхня відгуку в заданих межах змінювання факторів може мати кілька локальних екстремумів, за результатами однієї реалізації методу Бокса – Уїлсона не можна стверджувати, що знайдено глобальний екстремум. Серію експериментів за допомогою цього методу потрібно повторити кілька разів, починаючи рух із випадково вибраних і рівномірно розкиданих у факторному просторі точок.

Питання для самоконтролю

1. Що означає поняття «функція відгуку»?

2. В чому полягає проведення експериментів (натурних чи імітаційних) для пошуку оптимальних рішень?

3. Які Вам відомі способи знаходження екстремуму функції відгуку?

4. До чого зводиться задача пошуку екстремуму функції відгуку?

5. За яким методом можна виконувати оптимізацію систем? Поясніть сутність цього методу.

<== попередня сторінка	\|	наступна сторінка ==>
Перевірка адекватності моделі	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.