• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Об'єкти керування, їх математичні моделі. Характеристики об'єктів керування. Одноємнісні об'єкти. Багатоємнісні об'єкти. Об'єкти з розподіленими параметрами.

Об'єкти керування. Характеристики об'єктів

Будь-яка система автоматичного керування складається з керованого об'єкта і засобів керування. В об'єкті протікають керовані процеси і стан його визначається значеннями керованих параметрів, що залежать від керуючих впливів і впливу навколишнього середовища.

У загальному випадку об'єкт керування О можна представити схемою, наведеною на рис. 2.1, а. Тут сукупність керуючих впливів позначена вектором 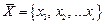, вплив зовнішнього середовища

Рис. 2.1. Функціональні схеми об'єктів керування: а — з багатьма керованими величинами; б — з одною керованою величиною.

– вектором , керовані величини – вектором . Якщо як об'єкт керування розглядати магістральний канал, розділений на б'єфи, то керованими величинами будуть рівні води в б'єфах, керуючими впливами – приплив води з джерела водозабору, зовнішніми впливами – витрати, опади, фільтрація й інші фактори.

Якщо об'єкт характеризується однією вихідною і однією керованою величиною, то він називається однозв'язним. В однозв'язних об'єктах зовнішні збурення прийнято поділяти на навантаження 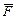і завади f, як це показано на рис. 2.1,б. Якщо вектори і 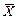мають кілька взаємозалежних координат, то об'єкт називається багатозв’язним.

Технологічний процес, що протікає в будь-якому об'єкті, характеризується визначеним зв'язком між векторами .

В усталеному режимі зовнішні впливи 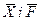не залежать від часу. Тому характеристиками об'єкта є залежності керованих величин від зовнішніх впливів:

. /2.1/

Залежність у=f(х) для однозв'язного об'єкта при сталому значенні і відсутності завад називається статичною характеристикою об'єкта. Залежність y=f(F) при х=const і відсутності завад називається навантажувальною характеристикою об'єкта.

Динамічний режим в об'єкті керування виникає при всякій зміні зовнішніх впливів і його вивчення зводиться до дослідження залежності Y(t) при заданих функціях X(t) і F(t). У цьому випадку рівняння /2.1/ приймає вид системи диференціальних рівнянь, що описують зміну кількості енергії або речовини в об'єкті. Здатність об'єкта накопичувати енергію або речовину характеризує ємність об'єкта. Якщо енергія або речовина накопичується в одному місці, то об'єкт називається одноємнісним і в динаміці він описується диференційним рівнянням першого порядку. Якщо в об'єкті накопичується енергія декількох видів, наприклад, механічна, теплова й електромагнітна, або речовина в декількох взаємозв’язаних місцях, то такий об'єкт називається багатоємнісним. Порядок диференційного рівняння, яким описується багатоємнісний об'єкт, дорівнює кількості взаємозалежних місць накопичення речовини або видів і місць накопичення енергії.

Статичні і динамічні характеристики об'єктів можна знайти аналітичними або експериментальними методами. Аналітичні методи вимагають глибоких знань динаміки процесів в різних режимах роботи об'єкта. Для експериментального зняття характеристик необхідні дослідні установки або їх фізичні моделі, а також спеціальна реєструюча апаратура. Тому аналітичним методам надають перевагу.

Розглянемо методику знаходження характеристик найбільше типових у гідромеліорації об'єктів керування.

Одноємнісні об'єкти

Найпростішим одноємнісним об'єктом є басейн (рис.2.2,а). Керуючим впливом х є приплив води Q₁; керованою величиною у - рівень Н, і навантаженням F — витрата води з басейну Q₂. Впливом завад (випаровуванням, фільтрацією, зміною атмосферного тиску й ін.) нехтуємо.

За цих умов для нескінченно малого проміжка часу dt рівняння матеріального балансу, що зв'язує величини Н, Q₁ і Q₂, запишеться у виді

, /2.2/

де Ω — площа поперечного перерізу басейну.

Рівняння /2.2/ являє собою математичний опис процесу, що відбувається в басейні при зміні припливу або витрати.

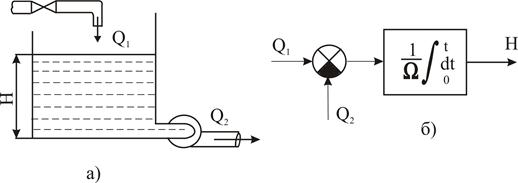
Рис. 2.2. Схема об'єкта керування без самовирівнювання (а) і його структурна схема (б).

Якщо Q₁ = const і Q₂ не залежить від Н, то рівняння /2.2/ лінійне. Об'єкт керування, який описується лінійним диференціальним рівнянням першого порядку, називається лінійним одноємнісним об'єктом.

Отже, басейн за умови Q₂ = const – лінійний одноємнісний об'єкт і його динамічна характеристика буде рішення рівняння /2.2/.

Інтегруючи /2.2/ для випадку 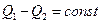, знаходимо

, /2.3/

де Н₀ – рівень води в басейні в початковий момент часу (t=0).

Вираз /2.3/ показує, що при зміні припливу або витрати рівень змінюється за лінійним законом.

Усталений режим у басейні характеризується Н=const і настає при Q₁ = Q₂. Усталене значення рівня можна знайти з рівняння /2.3/, якщо підставити в нього . При і Q₁ = Q₂ права частина рівняння /2.3/ перетворюється у невизначеність виду 0·∞. Таким чином, може приймати будь-яке значення в межах від нуля до максимального значення, рівного глибині басейну. Об'єкти керування, що мають таку властивість, називаються об'єктами без самовирівнювання.

Структурна схема об'єкта без самовирівнювання показана на рис. 2.2,б. Вона є розімкнутою і складається із сумматора й інтегруючої ланки.

При нульових початкових умовах (при 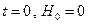) рівняння /2.3/ приймає вид

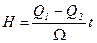/2.4/

і його називають кривою розгону. Відношення (Q₁-Q₂)/Q називається швидкістю розгону, тому що характеризує зміну рівня за одиницю часу.

Важливою характеристикою басейну є час спорожнення при Q₁=0. Його можна знайти, проінтегрувавши рівняння /2.2/ у межах від Н=Н₀ до Н=0:

, /2.5/

де W₀=ΩH₀ – об’єм води в басейні на початку спорожнення.

У басейні з вільним витіканням води через отвір (рис. 2.3, а)

, /2.6/

де ω - площа отвору; µ - коефіцієнт витікання; g - прискорення вільного падіння.

Рис. 2.3. Схема об'єкта керування з самовирівнюванням (а) і його структурна схема (б).

Підставивши в рівняння /2.2/ Q₂ згідно з рівнянням /2.6/, одержуємо

. /2.7/

Рівняння /2.7/ є нелінійним диференціальним рівнянням першого порядку. Тому басейн із вільним витіканням води через отвір називається нелінійним одноємнісним об'єктом.

Інтегруючи /2.7/ у межах від Н=Н₀ до Н=0 при Q₁ = 0, знаходимо час спорожнення:

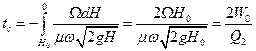, /2.8/

де Q₂ — витрата води при напорі Н₀.

З порівняння формул /2.5/ і /2.8/ випливає, що час спорожнення при вільному витіканні в два рази більший, ніж при сталій витраті.

Знайдемо рішення рівняння /2.7/. При заміні 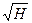на у рівняння /2.7/ зводиться до виду

, /2.9/

де .

Розділивши змінні в рівнянні /2.9/, одержуємо

. /2.10/

Інтегруючи /2.10/ при початкових умовах t₀ і, знаходимо динамічну характеристику нелінійного об'єкта

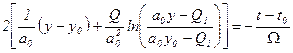
або

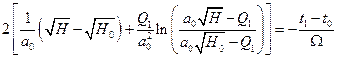. /2.11/

Рівняння /2.11/ є нелінійним трансцендентним рівнянням і показує, що рівень води в басейні є нелінійною функцією припливу Q₁. За цим рівнянням можна побудувати залежність H=f(t) для заданого значення Q₁.

Структурна схема об'єкта, який описується рівнянням /2.7/, наведена на рис. 2.3,б. Вона замкнена і складається із суматора, інтегруючої ланки і зворотного зв'язку.

Дія зворотного від’ємного зв'язку (гідростатичного тиску) призводить до того, що при зміні припливу рівень змінюється в меншій мірі, ніж при тій же умові в об'єкті без зворотного зв'язку. Крім того, після зняття зовнішнього впливу регульована величина з часом повертається до вихідного стану. Тому такі об'єкти називаються об'єктами із самовирівнюванням.

Аналіз динамічних процесів, що протікають в об'єктах, які описуються нелінійними рівняннями виду /2.11/, досить складний. Тому в теорії автоматичного керування вдаються до лінеаризації рівняння об'єкта, тобто до заміни нелінійного рівняння об'єкта наближеним лінійним рівнянням. Таке спрощення виправдане тим, що в системах автоматичного керування відхилення регульованого параметра об'єкта від заданого значення незначне.

Щоб лінеаризувати рівняння /2.7/, нелінійну залежність /2.6/ в околі точки (Q₂₀, Н₀) (рис. 2.4) замінимо лінійною, тобто приймемо

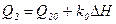, /2.12/

де – відхилення рівня від початкового значення Н₀; k₀ - коефіцієнт пропорційності між витратою і рівнем.

Для обчислення коефіцієнта k₀ залежність /2.6/ в околицях точки (Q₂₀, Н₀) розкладемо у ряд Тейлора й обмежимося двома його членами:

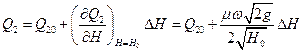. /2.13/

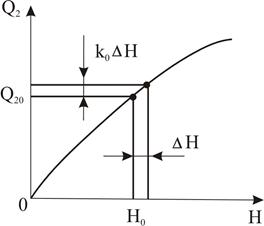
Рис. 2.4. Навантажувальна характеристика басейна.

Порівнюючи вирази /2.12/ і /2.13/, знаходимо

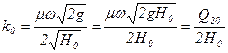. /2.14/

Заміняючи в /2.7/ нелінійний член лінійним згідно рівняння /2.12/ і враховуючи, що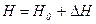, одержуємо

. /2.15/

Динамічну характеристику об'єкта при невеликому збільшенні припливу шукаємо в такий спосіб. Нехай при . У цьому випадку /2.15/ приймає вид

, /2.16/

тому що .

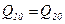Рівняння /2.16/ описує відхилення рівня води в басейні від усталеного значення і його прийнято записувати у виді

, /2.17/

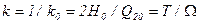де – стала часу об'єкта; – коефіцієнт підсилення об'єкта за керуючим впливом.

З порівняння виразу для сталої часу з рівнянням /2.8/ випливає, що стала часу басейну, з якого вода випливає під дією сили тяжіння, чисельно дорівнює часу спорожнення басейну.

Рішення рівняння /2.17/

/2.18/

називається перехідною функцією об'єкта.

Рівність /2.18/ показує, що при невеликому ступінчастому збільшенні припливу на рівень змінюється за експоненціальним законом і досягає усталеного значення 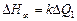. Оскільки стала часу Т і коефіцієнт підсилення k залежать від початкової витрати Q₂₀, то і перехідні функції для різних початкових значень Н₀ будуть різними.

На рис. 2.5, а наведена перехідна функція, яка побудована за рівнянням /2.18/, і показано, що піддотична у будь-якій точці цієї кривої чисельно дорівнює сталій часу Т. Якщо перехідна функція знята експериментально, то по ній легко визначити сталу часу і коефіцієнт підсилення .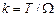

Рис. 2.5. Перехідні характеристики одноємнісного об'єкта: а – по керуючому впливі; б – по збуренню.

Статичну характеристику, зазвичай, знаходять з рівняння об'єкта, прирівнявши нулю всі похідні. Підставляючи у рівняння /2.17/ 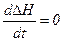, одержимо рівняння статичної характеристики:

/2.19/

або

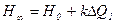. /2.20/

Рівняння /2.20/ показує, що статична характеристика при невеликих є лінійною і залежить від початкового значення рівня Н₀.

Розглянуті динамічні процеси викликані зміною керуючого впливу. При дії на об'єкт збурення, наприклад, зміни витрати, виникає перехідний процес, що також описується рівнянням /2.2/.

Витрату води з басейну можна змінювати шляхом зміни площі отвору. Якщо, наприклад, площа отвору збільшити на Δω, то витрата зросте на

, /2.21/

де Н₀ — рівень води в басейні до зміни площі отвору.

Підставивши /2.21/ в рівняння /2.2/ і провівши лінеаризацію, одержимо

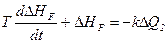. /2.22/

Рішення рівняння /2.22/

/2.23/

називається перехідною функцією об'єкта за збуренням. Це рівняння описує зміну рівня при ступінчастому збільшенні площі отвору (рис. 2.5,б). Щоб одержати перехідну функцію 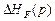при зменшенні площі отвору на , праву частину рівняння необхідно помножити на мінус одиницю.

Залежність

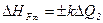/2.24/

являє собою навантажувальну характеристику об'єкта у відхиленнях від початкового значення рівня Н₀. У виразі /2.24/ знак плюс відноситься до зменшення , а мінус – до збільшення. З порівняння виразів /2.18/ і /2.23/ випливає, що при дії на об'єкт зовнішніх збурень (X або F) характер перехідного процесу не змінюється.

Багатоємнісні об'єкти

Крім одноємнісних, часто приходиться досліджувати багатоємнісні об'єкти. Прикладом багатоємнісного об'єкта може служити об'єкт, що складається з двох сполучених резервуарів (рис. 2.6). Динаміка такого об'єкта описується системою рівнянь

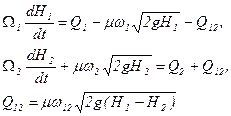/2.25/

за умови, що втратою напору в з’єднувальній трубі сталого поперечного перерізу можна знехтувати.

У розглянутому об'єкті кожний з векторів зовнішніх збурень і керованих величинах має по дві компоненти:

.

Τаκ як кожний із рівнів Н₁ і Н₂ залежить від Q₁, Q₂, Q_1р і Q_2p, то об'єкт багатозв’язаний. Речовина в ньому накопичується

Рис. 2.6. Схема двоємнісного об'єкта.

у двох місцях. Тому такий об'єкт називають двоємнісним.

Систему /2.25/ можна лінеаризувати описаним вище методом. Після лінеаризації перехідні функці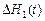ї і при дії одного із збурень будуть представляти рішення диференціального рівняння другого порядку. Динамічні і статичні характеристики елементів, які описуються диференціальним рівнянням другого порядку, докладно досліджуються в підрозділі 3.2 і тому тут не розглядаються.

Об'єкти з розподіленими параметрами

Розглянуті об'єкти керування відносяться до об'єктів із зосередженими параметрами, тому що керовані величини, наприклад рівні, приймаються однаковими у всіх точках об'єкта. Якщо відстань між розташуванням місць припливу і витрати у каналі велика, то рівні в кожен момент часу в різних точках будуть різними. Об'єкти, у яких керовані величини залежать від зовнішніх впливів і координат точок, називаються об'єктами з розподіленими параметрами. Такими об'єктами є довгий трубопровід, канал, меліороване поле тощо.

Динамічні процеси в об'єктах з розподіленими параметрами описуються диференціальними рівняннями з частковими похідними. Наприклад, довгий сталого перерізу трубопровід, по якому під тиском протікає ламінарний потік води й у якому можна знехтувати тертям, зміною швидкості звуку й іншими другорядними факторами, описується рівняннями Η. Ε. Жуковського:

, /2.26/

де а - швидкість звуку в трубопроводі; h=H/H_н і q=Q/Q_н - відносні зміни напору і витрати; Н_н і Q_н – номінальні значення; ; v – швидкість руху води.

Рішення системи /2.26/ залежить від граничних умов, що визначаються режимом роботи регулюючих пристроїв.

При зміні витрати в трубопроводі виникають хвилі тиску і швидкості, які поширюються уздовж трубопроводу зі швидкістю звуку і по черзі відбиваються від регулюючих пристроїв, що знаходяться на його кінцях. При швидкому закритті регулюючого пристрою під дією сил інерції водного потоку відбувається підвищення тиску, що потім у результаті відбивання багаторазово повторюється. Це явище називається гідравлічним ударом і часто стає причиною аварій.

Перехідні процеси в даному випадку складаються з послідовності процесів, що виникають у дискретні моменти часу t, 2t, 3t, ..., тобто в моменти відбивання хвиль від границь трубопроводу, де t - час проходження по трубопроводу звукової хвилі.

Якщо розглядати дію тільки першої хвилі, то перехідний процес у точці, яка знаходиться на віддалі х від місця прикладання зовнішнього впливу, можна записати у виді

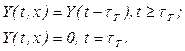/2.27

де Υ – перехідний процес у ланці з умовно зосередженими параметрами; – час транспортного запізнення, рівний часу поширення сигналу керування в конкретному середовищі — континуумі матеріальних точок, наприклад, у воді, ґрунті тощо, на відстань х. Це запізнення назване транспортним, очевидно, тому, що воно відображає рух матеріального середовища або носія інформації керування.

Ланка з умовно зосередженими параметрами являє собою об'єкт, у якому зовнішнє збурення розподілене по всьому континуумі точок.

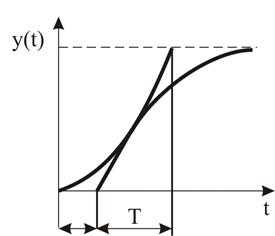
Рис. 2.7. Перехідна характеристика об'єкта з запізнюванням.

У ряді об'єктів керування після дії зовнішнього збурення сигнал на виході вимірювального пристрою спочатку змінюється дуже повільно, а потім – за законом, близьким до експоненціального (рис. 2.7). Це зумовлено як інерційністю вимірювального перетворювача, так і конструктивними особливостями об'єкта.

Графік на рис.2.7 можна наближено апроксимувати експонентою зі сталою часу Т і запізненням t, яке називають перехідним запізненням об'єкта.

Отже, процеси, що протікають в об'єктах керування, мають визначений математичний опис, який прийнято називати математичною моделлю об'єкта. Знання математичних моделей об'єктів необхідно як при проектуванні, так і при налагодженні систем автоматичного керування.

Переглядів: 4628