Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Комбінаторика

Вибірка елементів називається розміщенняміз n елементів по m елементів, якщо враховується порядок слідування, і комбінацієюіз n елементів по m елементів, якщо беруться до уваги тільки елементи без урахування порядку. Вибірки можуть допускати і не допускати повторення елементів. При

вибірках з повтореннями відрізняють два випадки. В першому випадку припускається, що запас елементів, які повторюються, обмежений і визначається специфікацією {n₁, n₂,…,n_k}, де n_i− кількість елементів i – го виду. Загальна кількість елементів початкової множини n = n₁ + n₂ +…+n_k, причому m ≤ n.

В другому випадку запас елементів не обмежується, і у вибірці із n елементів допускається будь-яке число повторень, яке не перевищує числа m. Початкову множину можна розглядати як таку, яка складається з різних елементів, але після вибірки деякого елемента він відновлюється в цій множині (вибірка з повторенням).

При m = n маємо 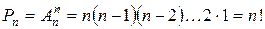Формулу для розміщень без повторень звичайно записують у вигляді .

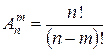Число різних переставлень з повтореннями із 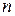елементів, специфікація яких {n₁, n₂,…,n_k}, причому n = n₁ + n₂ +…+n_k., виражається формулою

Приклад 1. Нехай є проекти трьох типів. Треба визначити, скільки існує різних планів забудови вулиці 10 будинками, якщо відомо, що мають бути три будинки І типу, п’ять будинків II типу і два будинки ІІІ типу.

Розв’язання. В даному випадку маємо переставлення з повтореннями, при цьому n₁ = 3, n₂ = 5, n₃=2, n = 3 + 5 + 2 = 10. Використовуючи останню формулу, знаходимо:

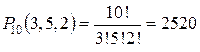Число розміщень з необмеженими повтореннями становить

Число комбінацій із n елементів по m елементів становить

Число комбінацій із n елементів по m елементів з необмеженими повтореннями

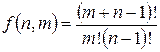Вираз

називається біномом Ньютона, а величини 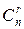називаються біноміальними коефіцієнтами.

Нехай дано N об’єктів і деяка сукупність властивостей цих об’єктів 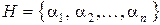. Позначимо через 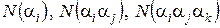і т.д. кількість об’єктів які мають відповідно властивості a_i ; a_i i a_j і т.д. елементів множини . Якщо враховуються об’єкти, які не мають властивостіa_i, то пишуть . Наприклад, означає число об’єктів, які мають властивості a₂ і a₅, але не мають властивості a₃.

Число об’єктів, які не мають жодної властивості із множини H, визначається формулою включення і виключення:

Формулу для числа об’єктів, які мають і не мають деякі властивості, можна подати у вигляді (при n = 4):

Приклад 2. Нехай загальне число об’єктів N = 38. Задані властивості:

a₁ − стальний, a₂ − чорний, a₃− сферичний, причому .

Число об’єктів, які не мають жодної властивості, .

Число стальних, але не чорних і не сферичних, становить

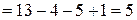Питання для самоперевірки

1.Сформулюйте правила вибору.

2.Дайте означення розміщень і комбінацій без повторень і з повтореннями.

3.Дайте означення переставлень без повторень і з повтореннями.

4.Що таке біном Ньютона?

5.В чому полягає правило включення і виключення?

Література: [1], c. 205-219; [2], c. 18-23.

Вправи

34.Скільки п’ятизначних чисел можна скласти з цифр 1, 2, 3, 4, 5 так, щоб жодна з них не повторювалась?

35. Скільки парних чотиризначних чисел, що складаються з цифр 2, 3, 5, 7 можна одержати, якщо повторення цифр у числах заборонені?

36. З цифр 1, 2, 3, 4, 5 складають різні тризначні та чотиризначні числа. Скільки таких чисел можна скласти, якщо повторення цифр у числах заборонені?

37. Студент забув останні три цифри потрібного телефону, але він пам’ятає, що всі три цифри різні, тому набирає їх навмання. Скількома способами він може набрати номер абонента?

38. Скільки різних слів можна одержати, переставляючи букви в словах: а) “коловорот”; б) “програма”?

39.У футбольній команді є 13 польових гравців і 2 воротарі. Скількома способами можна підібрати склад команди (11 гравців, в тому числі один воротар)?

40.Знайти число діагоналей n-кутника.

41. На площині дано n точок, з яких ніякі три не лежать на одній прямій за винятком m точок, які лежать на одній прямій. а) Скількома прямими можна з’єднати ці точки? б) Скільки існує різних трикутників з вершинами в даних точках?

42. Скільки різних натуральних чисел можна скласти з цифр 0, 1, 2, 3, 4, якщо в позначенні кожного числа кожна з даних цифр входить не більше одного разу?

43. Є 10 різних книг, кожна в 3 примірниках; скількома способами можна вибрати книги з числа даних?

44. Є 30 однакових предметів. Скількома способами можна розподілити ці предмети між 5 особами?

45. Із 30 співробітників відділу англійську мову знають 19, німецьку − 17, французьку − 11, англійську і німецьку − 12, англійську і французьку − 7, німецьку і французьку − 5, всі три мови − 2. Скільки співробітників відділу не володіють іноземними мовами? Скільки з них знають тільки англійську, тільки німецьку, тільки французьку мови ?

46. Довести тотожність .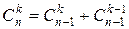

47. Довести, що сума біноміальних коефіцієнтів, взятих з почережними знаками, дорівнює нулю.

<== попередня сторінка	\|	наступна сторінка ==>
Загальні властивості відношень; функціональні відношення	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.