• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Загальні властивості відношень; функціональні відношення

Приклад 1. Нехай . Очевидно, що відношення функціональне. Але обернене відношення не є функцією.

Якщо функціональне відношення A = X ´ Y скрізь визначене на Х, то його називають відображенням множиниХ вY.

При відображенні Х в кожен елемент x із X має один і тільки один образ y = f(x) із Y. Однак, зовсім не обов’язково, щоб і будь-який елемент із Y був образом деякого елемента із Х. Якщо ж будь-який елемент із Y є образом хоч би одного елемента із Х, то кажуть, що має місце відображення Хна Y (сюр’єкція). Якщо для будь-яких двох різних елементів x₁ і x₂ із X їх образи

y₁ = f(x₁) і y₂ = f(x₂) також різні, то відображення f називається ін’єкцією. Відображення, яке є одночасно сюр’єктивним і ін’єктивним, називається бієкцією. В цьому випадку кажуть, що між елементами X і Y має місце взаємно-однозначна відповідність. При цьому обернене відношення f ^–1 також є взаємно-однозначним відображенням.

Питання для самоперевірки

1.Яке відношення називається функціональним?

2.Дайте означення сюр’єкції, ін’єкції, бієкції.

3.Що таке відношення еквівалентності?

4.Чи можна за графом або матрицею відношення дійти висновку про те, що це відношення еквівалентності?

5.Що таке відношення порядку?

6.Які множини називаються рівнопотужними, зліченними?

Література: [1], c. 86-106; [2], c. 15-18.

Вправи

26. Нехай A = {a, b, c} – множина бінарних відношень відповідно =, >,

< ; B ={1, 2, 3, 4, 5, 6} – множина шести загальних властивостей відношень (1− рефлексивність, 2 − антирефлексивність, 3 − симетричність, 4 − асиметричність, 5 − антисиметричність, 6 − транзитивність). Треба побудувати граф відношення від 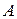до 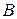, яке встановлює відповідність між бінарними відношеннями із 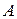і їх загальними властивостями із .

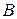27. На множині N = {1, 2, 3, 4, 5} задані відношення:

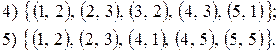
Які з цих відношень являються функціями і які − відображеннями?

28. До якого типу належать відображення із задачі 27?

29. Які з наведених нижче відношень на множині дійсних чисел R являються функціями

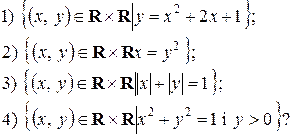
30. Показати, що кожна з наступних функцій має обернену (R –множина дійсних чисел):

а) 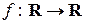, де ;

б) ;

в) .

31. Доведіть, що кожне з наступних відношень є відношенням еквівалентності:

а) подібність на множині всіх трикутників на площині;

б) належність до однієї групи на множині студентів факультету;

в) концентричність на множині кіл на площині.

32. Вкажіть властивості, які мають наведені далі відношення і поясніть, чому вони не є еквівалентностями:

а) “ x кратне y ” на множині цілих чисел;

б) “ x має спільні точки з y ” на множині прямих на площині;

в) “ x дотикається y ” на множині кіл на площині.

33. Доведіть, що наведені відношення є відношеннями порядку:

а) “ x важчий ніж y ” на множині деталей;

б) “ x знаходиться всередині y ” на множині кіл на площині.

Читайте також:

1. G. Дитячі функціональні гастроінтестінальні розлади: Новонароджені/діти раннього віку
2. I. Загальні збори АТ
3. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
4. I. Загальні положення
5. I. Загальні положення
6. I. ЗАГАЛЬНІ ПРАВИЛА.
7. II. Загальні вимоги до розробки екскурсії
8. II. ЗАГАЛЬНІ ПОЛОЖЕННЯ.
9. IV. Загальні висновки
10. IV. ЗАГАЛЬНІ ПОНЯТТЯ ПРО ПЕРШУ МЕДИЧНУ ДОПОМОГУ ПОТЕРПІЛИМ.
11. IV. Загальні рекомендації щодо безаварійної та безпечної експлуатації сільськогосподарської техніки вітчизняного та зарубіжного виробництва
12. Overall Reflection Properties - Загальні Властивості Віддзеркалення

Переглядів: 2710