• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні поняття теорії відношень

В загальному випадку відношення визначає який-небудь зв’язок між предметами або поняттями. Відношення між парами об’єктів називають бінарними.

Бінарне відношення між елементами двох множин встановлює відповідність елементів однієї множини X елементам іншої множини Y. Таке відношення може бути задане як множина упорядкованих пар (x, y), які є елементами множини X ´ Y.

Якщо A − відношення, то співвідношення xAy можна записати також у вигляді (x, y)ÎA, де A Ì X ´ Y. Наприклад, вирази 3 < 7 і (3, 7)Î< означають одне й те ж, однак, перший з них звичніший. В той же час вираз (7, 3)Î< означає 7<3, що неправильно. Таким чином, в загальному випадку переставляти елементи в парі (x, y) не можна, що і підкреслюється назвою пари − упорядкована. Елемент x називається першою координатою, а елемент y− другою координатою упорядкованої пари.

Областю визначення відношення A (позначення D_В) називається множина всіх перших координат, а областю значень (позначення D_З) − множина всіх других координат. Якщо xÎX i yÎY, то D_В (A)ÌX i D_З (A)ÌY В цьому випадку кажуть, що A є відношення від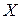до. Якщо Y = X, то будь-яке відношення xAy є підмножиною множини X´X і називається відношенням вX.

Окремі випадки відношень в X: 1) повнеабо універсальне відношенняP=X ´X,яке має місце для кожної пари (x₁, x₂) елементів із X (наприклад, відношення “вчитися в одній групі” на множині студентів даної групи); 2) тотожне(діагональне) відношення E, рівносильне x = x (наприклад, рівність на множині дійсних чисел); 3) порожнє відношення, яке не задовольняє жодна пара елементів з X(наприклад, відношення “бути братом” на множині жінок).

Очевидно, для будь-якого відношення A в X справедливо ÆÌ AÌ P.

Приклад 1. Нехай X={ 2, 3 } і Y={ 3, 4, 5, 6 }. Декартовий добуток цих множин X´Y ={(2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)}. Відношення "бути дільником" є множина A={(2, 4), (2, 6), (3, ), (3, 6)} відношення = є множина B={(3, 3)}, а відношення > є порожня множина Æ. Для відношення A то D_В (A)= {2, 3}= X, D_З (A)= {3, 4, 6}Ì Y.

Нехай X = {1, 2, 3}, Y = {1, 2, 3, 4, 5, 6, 7, 8, 9} і відношення А описується наступним чином: A={(x, y)ÎX´Y | y=x²}. Тоді A={(1, 1), (2, 4) (3, 9)}, D_В (A)= = {1, 2, 3}= X, D_З (A) = {1, 4, 9}=Y.

Нехай A Ì X´Y; якщо x_iÎ X, то переріз по x_i відношення A, який позначають A(x_i), є множина yÎY таких, що (x, y)Î A. Множина всіх перерізів відношення A називається фактор-множиною множини Y по відношенню A і позначається Y/A. Вона цілком визначає відношення A.

Приклад 2. Нехай X={x₁, x₂, x₃, x₄, x₅}; ={y₁, y₂, y₃, y₄} i задано відношення A= {(x₁, y₁), (x₁, y₃), (x₂, y₁), (x₂, y₃), (x₂, y₄), (x₃, y₁), (x₃, y₂), (x₃, y₄), (x₄, y₃), (x₅, y₂), (x₅, y₄)}. Тоді A(x₁)={y₁, y₃}; A(x₂)={y₁, y₃, y₄}; A(x₃)={y₁, y₂, y₄}; A(x₄)={y₃}; A(x₅)={y₂, y₄}.

Якщо записати під кожним елементом з X відповідний переріз відношення A, то елементи другого рядка утворюють фактор-множину Y/A:

.

Об'єднання перерізів по елементах деякої підмножини B Ì X є перерізом A (B) цієї підмножини, тобто Так, A(х₂,х₃) 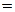A(х₂)Ս A (х₃)={y₁, y₂, y₃, y₄}. Таким чином, скінченне відношення можна подати за допомогою фактор-множини.

Інший спосіб − матричний− оснований на поданні відношення відповідною йому прямокутною таблицею (матрицею). Її стовпці відповідають першим координатам, а рядки− другим координатам. На перетині i-го стовпця і j-го рядка ставиться одиниця, якщо виконується співвідношення x_iAy_j, і нуль, якщо це співвідношення не виконується (нулеві клітинки можна залишати порожніми). Ця матриця містить всю інформацію про відношенняA.

Наприклад, для відношення, розглянутого в прикладі 2, матриця має вигляд:

.

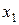
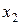
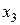
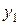
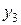
Відношення A^–1 називається симетричним (оберненим) до відношення AÌX´Y, якщо воно являє собою підмножину множини Y´X, утворену тими парами (y, x)ÎY´X, для яких (x, y)ÎA. Перехід від A до A^–1 здійснюється взаємною перестановкою координат кожної упорядкованої пари. Графи повного, тотожного і порожнього відношень зображені на рис. 1.4. Так, обернене відношення для “x є дільник y” буде “y ділиться на x”. При переході від A до A^–1 область визначення стає областю значень, і навпаки. Матрицю оберненого відношення одержують транспонуванням початкової матриці. Нехай дано три множини X, Y, Z і два відношення AÌX´Y і BÌY´Z. Композиція відношень A і B є відношення C = BA, що складається із всіх тих пар (x, z)Ì X´Z, для яких існує таке уÎY, що (x, у)Î A і (у, z)Î B. Переріз відношення C по х збігається з перерізом відношення B по підмножині A(х)Ì Y, тобто = B(A(х)).

Композиція відношень підпорядкована асоціативному закону, тобто D(BA)) = (DB) A = DBA, але не комутативна, тобто BA ≠ AB. Аналогічно можна одержати матрицю композиції C = BA як добуток матриць відношень матриць В і А, який знаходиться за правилом множення прямокутних матриць з наступною заміною відмінного від нуля елемента матриці одиницею.

Приклад 1.5. Нехай X={x₁, x₂, x₃, x₄, x₅}; Y={y₁, y₂, y₃, y₄}; A= {(x₁,y₁), (x₁, y₃), (x₂, y₁), (x₂, y₃), (x₂, y₄), (x₃, y₁), (x₃, y₂), (x₃, y₄), (x₄, y₃), (x₅, y₂), (x₅, y₄)}; B= {(y₁, z₂), (y₂, z₁), (y₂, z₂), (y₃, z₃), (y₄, z₃)}. Треба знайти матрицю композиції відношень C=BA.

Розв’язання. Одержимо матрицю композиції:

=

=

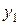
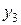
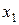
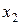
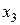
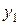
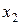
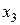
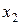
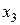
Питання для самоперевірки

1.Що таке бінарне відношення?

2.Що таке фактор множина?

3.Що таке повне, тотожне і порожнє відношення?

Література: [1], c. 81-86; [2], c. 11-15.

Вправи

22. Задані дві множини X = {x₁, x₂, x₃, x₄, x_5, x₆} і Y = {y₁, y₂, y₃, y₄ } і визначене бінарне відношення

.

Треба для відношення A:

а) написати область визначення і область значень;

б) визначити перерізи по кожному елементу із X;

в) написати матрицю і нарисувати граф;

г) визначити симетричне відношення.

23. Нехай X − множина студентів; Y – множина дисциплін і співвідношення xAy означає “студент x вивчає дисципліну y”. Треба дати словесний опис областей визначення і значень, перерізів і оберненого відношення, одержаних в задачі 22.

24.За результатами задачі 22 треба визначити множини і дати їм словесний опис у відповідності з умовою задачі 23.

25. Написати композицію C = BA відношень A = {(1, 2), (1, 3),(2, 1),

(2, 4), (3, 3)} і B = {(1, 1) (1, 3), (2, 2), (2, 3), (3, 1) (4, 2), (4, 3)}. Перевірити результат за допомогою операцій над матрицями.

Читайте також:

1. I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
2. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
3. II. Основні засоби
4. II. ОСНОВНІ ПОВНОВАЖЕННЯ ТРУДОВИХ КОЛЕКТИВІВ
5. II. Поняття соціального процесу.
6. II.3. Основні способи і прийоми досягнення адекватності
7. III. Основні обов'язки робітників та службовців
8. IV. ЗАГАЛЬНІ ПОНЯТТЯ ПРО ПЕРШУ МЕДИЧНУ ДОПОМОГУ ПОТЕРПІЛИМ.
9. IV. Основні обов'язки адміністрації
10. V. ОСНОВНІ ВИМОГИ ДО ОФОРМЛЕННЯ КУРСОВОЇ РОБОТИ
11. V. Поняття та ознаки (характеристики) злочинності
12. VII. ОСНОВНІ ЕТАПИ РОЗВИТКУ УКРАЇНСЬКОЇ КУЛЬТУРИ У ХХ ст.

Переглядів: 1791