Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Алгебра множин

Об’єднанняммножин 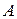і 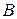(AՍB) називається множина всіх елементів, які належать множині A або множині B (або обом одночасно). Наприклад, {1, 2, 3} Ս {1, 3, 8} = {1, 2, 3, 8}.

Перерізом множин A і B (AՈB) називається множина всіх елементів, які належать одночасно і множині A, і множині B. Наприклад, {1, 2, 3}Ո{1, 3, 8}= ={1, 3}.

Різницею множин I A і B (A – B) називається множина всіх елементів, які належать множині A, але не належать множині B. Наприклад, {1, 2, 3} – {1, 3, 8} = {2}.

Звичайно, всі множини, якими оперують в тому або іншому випадку, є підмножинами деякої фіксованої множини U, яка називається універсальною (або універсумом). Так, для арифметики універсумом є числа, для зоології− світ тварин і т. п. Різниця 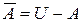називається доповненням множиниA. Воно містить всі елементи універсуму, крім елементів множиниA.

Диз’юнктивною сумою множин A і B (A + B) називається множина всіх елементів, які належать множині A або множині B, але не обом разом. Наприклад, {1, 2, 3}Ս{1, 3, 8} = {2, 8}.

Властивості операцій над множинами:

1.Комутативний закон для об’єднання AՍB =B ՍA і для перерізу AՈB= =BՈA.

2.Асоціативнийзакон для об’єднання AՍ(BՍC ) = (AՍB)ՍC і для перерізу AՈ(BՈC)=(AՈB)ՈC.

3. Дистрибутивнийзакон для об’єднання AՍ(BՈC) = (AՍB)Ո(AՍC) і для перерізу AՈ(BՍC) = (AՈB)Ս(AՈC).

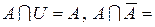4. Співвідношення, які характеризують властивості порожньої множини і універсуму відносно об’єднання AՍÆ і відносно перерізу Æ, AՈÆ 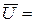= Æ, Æ.

5. Закони ідемпотентностідозволяють записувати формули з множинами без коефіцієнтів і показників степеня: AՍA=A, AՈA=A.

6. Закони поглинання: AՍ(AՈB )=A, AՈ(AՍB)=A.

7. Теореми де Моргана: .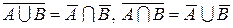

8. Співвідношення, які характеризують властивості доповнення, різниці, диз’юнктивної суми, включення і рівності: якщо AՍB = U і AՈB = Æ, то ; 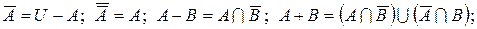A+B = B+A; (A+B)+C = A+(B+C) A+Æ = Æ+A = A; A Ì B тоді і тільки тоді, коли AՈB =A або AՍB = B або 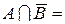Æ; A = B тоді і тільки тоді, коли 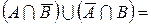Æ.

Доведення цих тотожностей основане на відношенні належності. Щоб переконатися, наприклад, в справедливості тотожності AՍ(BՈC) = (AՍB)Ո(BՈC), припустимо, що xÎAՍ(BՈC), тоді xÎA або xÎBՈC. Якщо xÎA, то x належить об’єднанню A з будь-якою множиною, отже, xÎAՍB і xÎAՍC. Але тоді x належить перерізу множин AՍB і AՍC, тобто xÎ(AՍB)Ո(AՍC). Якщо xÎBՈC, то xÎB і xÎC, отже, xÎAՍB і xÎAՍC, тобто і в цьому випадку x є елементом перерізу тих самих множин. Таким чином, доведено, що AՍ(BՈC) Ì (AՍB)Ո(BՈC.

Аналогічно доводиться і співвідношення AՍ(BՈC) É (AՍB)Ո(BՈC. Одержані результати означають, що AՍ(BՈC) = (AՍB)Ո(BՈC.

Властивості 1 − 7 представлені парами двоїстих (дуальних) співвідношень, одне з яких можна одержати з другого заміною в ньому символів: Ս на Ո і Ո на Ս, а також Æ на U і U на Æ.

Відповідні пари символів Ս, Ո і Æ , U називаються двоїстими (дуальними) символами.

При заміні в будь-якій теоремі символів, які входять в неї, дуальними одержимо нове твердження, яке теж є теоремою (принцип двоїстості або дуальності). Тотожність якщо AՍB=U і AՈB = Æ, то не змінюється при заміні символів дуальними, тому її називають самодвоїстою.

Алгебра множин знаходить широке застосування для тотожних перетворень, за допомогою яких можна спрощувати або перетворювати до зручнішого вигляду різні вирази, що складаються з множин. Такі перетворення здійснюються послідовним застосуванням відповідних властивостей операцій над множинами.

Приклад 1. Спростити вираз .

Розв’язання. Використовуючи закон дистрибутивності і властивість порожньої множини, одержимо 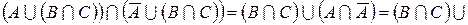Æ .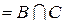

Питання для самоперевірки

1.Дайте означення операцій об’єднання, перерізу, різниці, доповнення, диз’юнктивної суми.

2.Сформулюйте комутативний, асоціативний та дистрибутивний закони ( відносно об’єднання і перерізу).

3.Назвіть основні методи доведення тотожностей алгебри множин.

4.Доведіть методом належності теореми де Моргана.

Література: [1], c. 20-22; [2], c. 8-11.

Вправи

13.Чи правильно, що А - В = В - А? Якщо Ви вважаєте, що в загальному випадку це неправильно, то чи можете Ви вказати окремий випадок, коли це твердження все-таки правильне? Чи це твердження завжди хибне?

14. Для будь-якої множини А що являє собою ?

15. Якщо АÌ В, то яке А - В?

16. Дано універсальну множину U = {a, b, c, d, e, f} та її підмножини:

P = { a, b, c, d }; Q = { a, c }; R = { b, d, e, f }. Напишіть елементи, що утворюють наступні множини: а) U Ո(Q Ս R); б) (PՈQ) Ս (P Ո R); в) ;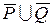

г) (P – R) – (Q – R); д) (Q ՍR )ՍÆ.

17. Довести за допомогою кругів Ейлера, що

а) ;

б) .

18. Дано універсальну множину U = {1, 2, 3, 4, 5, 6} та її підмножини

P = {1, 2, 3}; Q = {x ê4 ≤ x ≤ 6}; R = {2, 4,6}. Напишіть елементи, що утворюють множину

а) ;

б) ;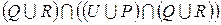

в) ;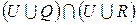

19. Виходячи із відношення належності, доведіть справедливість співвідношень:

а)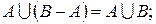

б) ;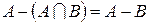

в) .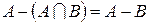

20.Доведіть тотожності:

а)

б)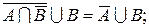

в) ;

г)

д) ;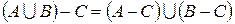

є) ;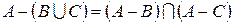

ж) ;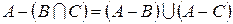

з) ;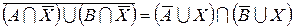

і) ;

й)

21. Спростіть вирази:

а)

б)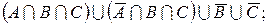

в)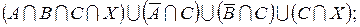

г)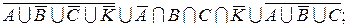

д)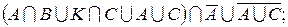

е) ;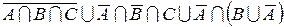

є) ;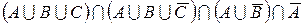

ж) ;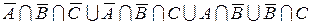

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Основні поняття теорії множин	\|	Основні поняття теорії відношень

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.