Тиск під зігнутою поверхнею рідини

Розглянемо поверхню рідини, що спирається на деякий плоский контур (рис.3а). Якщо поверхня рідини не плоска, то прагнення її до скорочення приведе до виникнення тиску, додаткового до того, який має рідина з плоскою поверхнею. У разі опуклої поверхні цей додатковий тиск позитивний (рис.3б), у разі ввігнутої поверхні – негативний (рис.3в). В останньому випадку поверхневий шар, намагаючись скоротитися, розтягує рідину.

Величина додаткового тиску, очевидно, повинна зростати із збільшенням коефіцієнта поверхневого натягу і кривизни поверхні. Обчислимо додатковий тиск для сферичної поверхні рідини. Для цього поділимо сферичну краплю рідини радіуса R діаметральною площиною на дві півкулі. Через поверхневий натяг обидві півкулі притягуються один до одного з силою, рівною . Ця сила притискує одну до одної обидві півкулі по поверхні площею 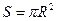і, отже, обумовлює додатковий тиск , тобто :

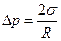
(4)

Аналогічна формула справедлива і для ввігнутої поверхні будь-якої форми, якщо тільки під 1/R розуміти середню кривизну поверхні. Середня кривизна визначається через кривизну нормальних перерізів. Нормальним перерізом поверхні в деякій точці називається лінія перетину цієї поверхні з площиною, що проходить через нормаль до поверхні в розглядуваній точці. У загальному випадку різні нормальні перерізи, проведені через одну і ту ж точку, мають різну кривизну. У геометрії доводиться, що півсума зворотних радіусів кривизни для будь-якої пари взаємно перпендикулярних нормальних перерізів має одне і те ж значення. Ця величина і є середня кривизна поверхні в даній крапці. Підставивши в (1) значення середньої кривизни, одержимо формулу для додаткового тиску під довільною поверхнею:

Ця формула називається формулою Лапласа.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Короткі теоретичні відомості	\|	Явища на межі рідини і твердого тіла

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.018 сек.