• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Випадок лінійного тертя

Лінійна залежність сил тертя від швидкості руху часто використовується в механічних системах (рис. 2.1) і описує в'язке тертя при невеликих швидкостях.

Рисунок 2.1 - Пружинний маятник з демпфером

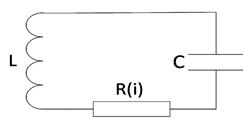
Рисунок 2.2 – Електричний контур з опором

Для електричних систем випадок лінійного тертя відповідає наявності омічного опору (рис.2.2) при лінійності консервативних параметрів.

Диференціальне рівняння руху системи в узагальнених координатах набуде вигляду

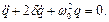(2.1)

Кількісне дослідження рішення рівняння (2.1) проводиться легко. Характеристичне рівняння, відповідне рівняння (2.1), має коріння

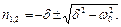(2.2)

Розглянемо два випадки.

а) Випадок слабкого опору характеризується умовою 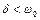. Корені рівняння (2.2) є комплексними:

де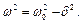

Тоді загальний розв'язок рівняння (2.1) можна записати у вигляді

(2.3)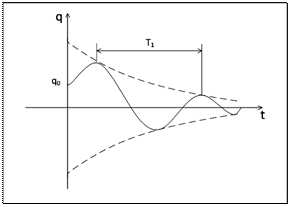

Рисунок 2.3 – Коливання лінійного слабодиссипативного осцилятора

Коливання, що відбуваються за законом (2.3), називають затухаючими коливаннями. Графік цих коливань зображений на

рис. 2.3. Огинаючі кривої процесу визначаються функціями Проміжок часу

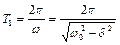(2.4)

прийнято називати періодом затухаючих коливань. З (2.4) випливає, що при наявності лінійної дисипації період коливань збільшується і не залежить від амплітуди.

Послідовність максимальних відхилень відповідає закону геометричної прогресії, тому що згідно (2.3)

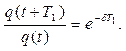
Модуль натурального логарифма цього відношення 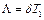називають логарифмічним декрементом, який служить зручною кількісною характеристикою темпу загасання вільних коливань.

б) Випадок сильного опору:

Загальне рішення рівняння (2.1) запишеться вигляді:

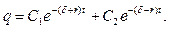(2.5)

Так як коріння де 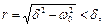завжди негативні, то рух, що описується (2.5) - неколивальний (рис.2.4). Система монотонно наближається до рівноважного стану при будь-яких початкових умовах.

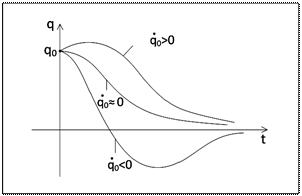
Рисунок 2.4 – Графік аперіодичних рухів при сильному лінійному терті

Переглядів: 469