Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Вимушені коливання нелінійного дисипативної осцилятора

Отримання замкнутих рішень задач про вимушені коливання при нелінійно-в'язкому терті або нелінійній відновлювальній силі навіть у разі моногармонічній обурюючий силі дуже важко. Навіть при застосуванні потужного методу пошука рішення у вигляді рядів Фур'є багато суттєві особливості поведінки нелінійних систем не виявляються досить виразно. Тому обмежимося деякими приватними випадками і окремими прийомами, що дозволяють з'ясувати найбільш характерні особливості даного явища.

3.2.1 Консервативна система з нелінійної відновлювальної силою

Розглянемо найпростішу нелінійну консервативну систему, описувану рівнянням

(3.5)

Приймемо, що система мало відрізняється від лінійної і тому вимушені коливання відбуватимуться з основною частотою

Будемо цікавитися тільки поведінкою амплітуди В. Якщо шукати вимушене рішення у вигляді то рівняння (3.5) прийме вигляд

. (3.6)

Рішення цього рівняння можна отримати графічним способом: визначення точок перетину прямої і графіка заданої функції 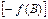(рис.3.5).

Рисунок 3.5 – Графічне визначення амплітуди вимушених коливань

Рисунок 3.6 – Характерна резонансна крива систем з нелінійною відновлювальною силою

Для різних та можна побудувати певний аналог резонансних кривих для лінійних систем. Зобразимо резонансну криву (рис.3.6) для деякої заданої амплітуди впливу і відзначимо особливості її поведінки. При отримаємо криву (скелетна крива - штрихова лінія), відповідну зв'язку власної частоти і амплітуди вільних коливань.

Аналіз характерною резонансної кривої дозволяє зробити наступні висновки:

1. При частоті 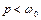в системі завжди відбувається однозначно визначений коливальний рух з амплітудою, яка залежить від частоти.

2. При можливі три режими руху:

, , .

Детальні дослідження показують, що два перших режиму стійкі, а третій режим нестійкий.

3. Відзначається неоднозначність протікання явища в залежності від напрямку зміни частоти збуджуючої. Поступове збільшення частоти від нуля призводить до збільшення амплітуди слідуючи гілки I. При деякому значенні система відчуває «зрив» амплітуди на гілку II (точки і 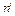) і далі амплітуда зменшується слідуючи кривій II. Якщо ж після зриву амплітуди частоту зменшувати, то буде зростання амплітуди до точки , а її подальше зменшення призводить до зриву на гілку I (точка );

4. При наявності тертя обидві гілки кривої сходяться і при збільшенні частоти зрив амплітуд стає неминучим.

3.2.2 Дисипативний осцилятор з нелінійним загасанням

А) Випадок механічної системи з нелінійно-в'язким тертям. Метод енергетичного балансу.

Диференціальне рівняння руху має вигляд

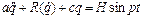. (3.7)

Наближене рішення рівняння вимушених коливань можна знайти методом енергетичного балансу, суть якого полягає в заміні нелінійної сили еквівалентною в енергетичному відношенні лінійною силою . Коефіцієнт визначається з умови рівності робіт, що здійснюються обома силами за один період, тобто

. (3.8)

Більше того, наближено приймаємо, що встановлено рішення (3.7) як і у випадку лінійного тертя, має вигляд

. (3.9)

Записуючи рівняння (3.8) для напівперіоду (оскільки швидкість 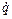не змінює знак), і підставляючи (3.9) в (3.8), знаходимо

, (3.10)

де .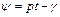

Якщо взяти для сили тертя нелінійний закон виду

то (3.10) дає значення

, (3.11)

де – ейлеров інтеграл другого роду.

Звертаючись до відомого рішенням лінійної задачі (див. 3.1) знаходимо рівняння для амплітуди

; (3.12)

тут . Задаючись тепер конкретним значенням нелінійності “ ”, “ ”, 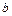можна побудувати при різних сімейство резонансних кривих.

Б) Контур з нелінійним загасанням. Метод гармонійного наближення.

Схема контуру представлена на рис. 3.7.

Рисунок 3.7– Схема контуру з нелінійним загасанням

Нехай

Тоді рівняння, що описує поведінку контура, в безрозмірному вигляді прийме вигляд:

, (3.13)

де , , , , , , .

У гармонійному наближенні рішення шукаємо у вигляді

. (3.14)

З (3.13) отримуємо систему для визначення , ,

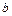
, (3.15)

(3.16)

(3.17)

де .

Перше рівняння (3.15) дає величину постійної напруги зміщення на ємності за рахунок несиметрії нелінійного опору. Рівняння (3.16) і (3.17) дозволяють знайти амплітуду вимушених коливань

або

. (3.18)

Задаючись параметрами впливу і , сімейство резонансних кривих отримуємо з (3.18).

Залишаючи питання побудови резонансних кривих на самостійне дослідження, зазначимо лише на вимогу обережності в передбачуваних висновках про вимушені коливання у нелінійних системах внаслідок прийнятих припущень, покладених в основу знайдених рішень.

Наприкінці даного розділу вкажемо ще на один метод (метод повільно мінливих амплітуд) аналізу поведінки слабонелінейних систем при гармонійному зовнішньому впливі. З основами методу читач може ознайомитися у відомих навчальних посібниках [1-4].

КОНТРОЛЬНІ ЗАПИТАННЯ І ЗАВДАННЯ ДО РОЗДІЛУ 3

1. Яким чином можна знайти час встановлення коливань?

2. Час розгойдування системи більше за наявності або відсутності опору? Відповідь обгрунтуйте.

3. Чи залежить частота вимушених коливаннь від характерис-тик коливальної системи?

4. Отримайте рішення вимушених коливань системи без дисипації у разі резонансу.

5. Якою особливістю володіє залежність амплітуди вимушених коливань від частоти впливу, що обурює в нелінійних системах?

<== попередня сторінка	\|	наступна сторінка ==>
Вимушені коливання в лінійних системах при гармонійній обурюючий силі	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.008 сек.