- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
КІЛЬКІСНІ КРИТЕРІЇ ОЦІНЮВАННЯ ТОЧНОСТІ ВИМІРІВ
3.1. Моделі розподілу випадкових похибок вимірів|вимірів|
Вище було показано, що випадкова похибка є|з'являється| наслідком впливу на результат вимірів різних випадкових взаємопов'язаних чинників|факторів|. Її можна інтерпретувати як алгебраїчну суму безлічі елементарних випадкових похибок.
Проаналізуємо процес формування випадкових похибок на прикладі|зразку| вимірювання|виміру| перевищення при геометричному нівелюванні. Для цього розглянемо|розглядуватимемо| випадкові похибки округлення відліку, узятого по рейці із точністю до 1 мм. Задамо інтервал вимірів|вимірів|, і вважатимемо|гадатимемо|, що вимірювання|виміри| виконують в інтервалі від -0,5 до +0,5 (рис.3.1).
Усі можливі значення похибок округлення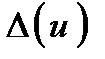 
укладаються|вкладаються| в десять|десятеро| фіксованих рівно імовірних інтервалів:
1) [- 0,5 – - 0,4]; 2) [- 0,4 – - 0,3]; 3) [- 0,3 – - 0,2]; 4) [- 0,2 – - 0,1];
5) [- 0,1 –| 0]; 6) [0 – 0,1]; 7) [0,1 –| 0,2]; 8) [0,2 – 0,3]; 9) [0,3 – 0,4];
10) [0,4 – 0,5].
Тут квадратними дужками позначені інтервали округлення на осі Δ(u). Ймовірність потрапляння похибок округлення у будь-який з інтервалів, представлених|уявляти| на рис. 3.1, дорівнює 0,1.
| Р |
| -0,5 |
|
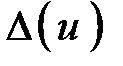
| Можливі похибки округлення |
| Інтервал вимірів|вимірів| |
| 0,4 |
| 0,3 |
| 0,2 |
| 0,1 |
| -0,1 |
| -0,2 |
| -0,3 |
| -0,4 |
| 0,5 |
Рис. 3.1 – Рівномірний розподіл помилок вимірів
Процес округлення вимірів має дискретний характер|вдача| і тому при оцінюванні точності вимірів у певному випадку можна скористатися відомими з|із| теорії ймовірності властивостями закону рівномірного розподілу випадкових величин (вимірів): функцією ймовірності, функцією розподілу, математичним очікуванням|чеканням|, медіаною та ін.
Відзначимо|помітимо|, що так само будуть розподілені елементарні похибки округлення відліків по горизонтальному і вертикальному кругу теодоліта, відліків по рейці при визначенні відстаней нитковим далекоміром, відліків рахункового механізму планіметра і в інших випадках геодезичної практики.
Відомо, що перевищення дорівнює різниці відліків h = uз – uп. Усі можливі значення похибок округлення Δ(h) обчисленого|обчисляти| перевищення наведені
в табл. 3.1.
Таблиця 3.1 – Значення можливих похибок округлення
| Δ(h) | -0,5 | -0,4 | -0,3 | -0,2 | -0,1 | +0,1 | +0,2 | +0,3 | +0,4 | +0,5 | |
| -0,5 | -0,1 | -0,2 | -0,3 | -0,4 | -0,5 | -0,6 | -0,7 | -0,8 | -0,9 | -1,0 | |
| -0,4 | +0,1 | -0,1 | -0,2 | -0,3 | -0,4 | -0,5 | -0,6 | -0,7 | -0,8 | -0,9 | |
| -0,3 | +0,2 | +0,1 | -0,1 | -0,2 | -0,3 | -0,4 | -0,5 | -0,6 | -0,7 | -0,8 | |
| -0,2 | +0,3 | +0,2 | +0,1 | -0,1 | -0,2 | -0,3 | -0,4 | -0,5 | -0,6 | -0,7 | |
| -0,1 | +0,4 | +0,3 | +0,2 | +0,1 | -0,1 | -0,2 | -0,3 | -0,4 | -0,5 | -0,6 | |
| +0,5 | +0,4 | +0,3 | +0,2 | +0,1 | -0,1 | -0,2 | -0,3 | -0,4 | -0,5 | ||
| +0,1 | +0,6 | +0,5 | +0,4 | +0,3 | +0,2 | +0,1 | -0,1 | -0,2 | -0,3 | -0,4 | |
| +0,2 | +0,7 | +0,6 | +0,5 | +0,4 | +0,3 | +0,2 | +0,1 | -0,1 | -0,2 | -0,3 | |
| +0,3 | +0,8 | +0,7 | +0,6 | +0,5 | +0,4 | +0,3 | +0,2 | +0,1 | -0,1 | -0,2 | |
| +0,4 | +0,9 | +0,8 | +0,7 | +0,6 | +0,5 | +0,4 | +0,3 | +0,2 | +0,1 | -0,1 | |
| +0,5 | +1,0 | +0,9 | +0,8 | +0,7 | +0,6 | +0,5 | +0,4 | +0,3 | +0,2 | +0,1 |
Усього можливе 121 значення похибок округлення в межах усього інтервалу вимірів|вимірів| [-0,5 – +0,5], які можна об'єднати в 21 групу рівних значень, враховуючи, що ймовірність округлення вимірів|вимірів| в межах одного інтервалу, наприклад [-0,5 – -0,4] або [+0,5 – +0,4] або [+0,1 – +0,2] вища, ніж ймовірність округлення в інтервалах [-0,5 – -0,3] або [-0,5 – -0,2] або [+0,1 – +0,5] і таке інше. Ймовірність таких округлень розподілена за законом Сімпсона, «трикутник розподілу». Аналітичний вираз|вираження| трикутного розподілу Сімпсона, характеристична функція і його властивості наведені в додатку Б|застосуванні|.
Для наведеного вище прикладу|зразка| випадкових похибок округлення розподіл Сімпсона показаний на рис. 3.2.
| -1 |
| Δ(h) |
| Р=0,1 |
| +1 |
| «Трикутник розподілу» Сімпсона |
| Р |
| Похибки округлень |
Рис. 3.2 – Ілюстрація розподілу похибки округлень
на інтервалі вимірів [-0,5 – +0,5]
Як приклад|зразок| наведемо табл. 3.2, де в чисельному вигляді|виді| представлені|уявляти| співвідношення похибок округлення і ймовірність їх появи.
У геометричному нівелюванні перевищення на станції вимірюють|виміряють| двічі, за основною (чорною) і додатковою (червоною) сторонами рейки. За остаточний результат виміряного|виміряти| перевищення вважають середнє значення. Для середнього перевищення h можливо N=1212=14641 варіантів випадкової елементарної похибки округлення. Усю множину значень можна об'єднати в 21 інтервал групування, як це показано в правій частині|частці| табл. 3.2. За даними цієї таблиці побудуємо|спорудимо| криву розподілу випадкових похибок вимірів|вимірів| (рис. 3.3.), що виражає|виказує| деяку функцію f (Δ).
Таблиця 3.2 – Приклад|зразок| числових співвідношень ймовірності і величин
похибки округлення
| Значення середини інтервалу | Діапазон значень в інтервалі | Обчислене|обчисляти| перевищення на станції | Середнє перевищення на станції | ||
| Кількість випадків h | Вірогідність | Кількість випадків h | Вірогідність | ||
| - 1,0 | -1,05 – -0,95 | 0,0083 | 0,002 | ||
| - 0,9 | -0,95 – -0,85 | 0,0165 | 0,0015 | ||
| - 0,8 | -0,85 – -0,75 | 0,0248 | 0,0050 | ||
| - 0,7 | -0,75 – -0,65 | 0,0331 | 0,0117 | ||
| - 0,6 | -0,65 – -0,55 | 0,0413 | 0,0229 | ||
| - 0,5 | -0,55 – -0,45 | 0,0496 | 0,0393 | ||
| - 0,4 | -0,45 – -0,35 | 0,0579 | 0,0600 | ||
| - 0,3 | -0,35 – -0,25 | 0,0661 | 0,0818 | ||
| - 0,2 | -0,25 – -0,15 | 0,0744 | 0,1014 | ||
| - 0,1 | -0,15 – -0,05 | 0,0826 | 0,1156 | ||
| -0,05 – +0,05 | 0,0909 | 0,1210 | |||
| + 0,1 | +0,05 – +0,15 | 0,0826 | 0,1156 | ||
| + 0,2 | +0,15 – +0,25 | 0,0744 | 0,1014 | ||
| + 0,3 | +0,25 – +0,35 | 0,0661 | 0,0818 | ||
| + 0,4 | +0,35 – +0,45 | 0,0579 | 0,0600 | ||
| + 0,5 | +0,45 – +0,55 | 0,0496 | 0,0393 | ||
| + 0,6 | +0,45 – +0,55 | 0,0413 | 0,0229 | ||
| + 0,7 | +0,55 – +0,65 | 0,0331 | 0,0117 | ||
| + 0,8 | +0,75 – +0,85 | 0,0248 | 0,0050 | ||
| + 0,9 | +0,85 – +0,95 | 0,0165 | 0,0015 | ||
| + 1,0 | +0,95 – +1,05 | 0,0083 | 0,0002 | ||
| 1,0001 | 0,9998 |
Відзначимо очевидні властивості цієї функції:
1. Функція завжди позитивна і симетрична щодо|відносно| осі ординат.
2. Функція має максимум у точці Δ = 0, де похідна функції f '(Δ) = 0.
3. Зі збільшенням абсолютної величини Δ функція f (Δ) асимптотично наближається до осі Δ.
4. Позитивним значенням Δ відповідають негативні|заперечні| значення f '(Δ), а негативним|заперечним| – позитивні значення f '(Δ), тобто має місце нерівність f '(Δ)·Δ < 0.
5. Представлені|уявляти| в правій частині|частці| табл. 3.2 ймовірності вичерпують усі можливі значення f (Δ). Отже, площа|майдан| фігури, обмежена віссю Δ і кривою має дорівнювати одиниці.
Перерахованим вище умовам відповідає функція, рівняння якої має вигляд:
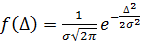(3.1)
| f (Δ) |
Рис. 3.3 – Нормальний закон розподілу
Параметр σ в (3.1) визначає|уявляє| стандарт, який був викладений у попередньому підрозділі. Чим менше σ, тим тісніше групуються значення Δ щодо|відносно| осі f (Δ).
Розподіл випадкових похибок, представлений|уявляти| функцією (3.1), називають нормальним розподілом.
У розглянутому|розглядувати| вище прикладі|зразку| досліджувалося лише одне джерело формування випадкових похибок – похибок округлення відліку. Однак відомо, що на точність вимірювання|виміру| перевищення методом геометричного нівелювання окрім похибок округлення впливають також похибки, зумовлені випадковими коливаннями візирної осі приладу, коливаннями зображення рейки внаслідок|внаслідок| рефракції та інші чинники|факторами|.
Аналогічне явище має місце і в інших видах геодезичних вимірів|вимірах| – горизонтальних і вертикальних кутів|рогів| і напрямів|направлень|, довжин ліній і так далі. Усе це дає підставу|основу| розглядати|розглядувати| нормальний розподіл (3.1) як універсальний закон імовірнісного розподілу випадкових похибок.
3.2. Моделі розподілу систематичних похибок вимірів|вимірів|
Систематичні похибки, геодезичних вимірів|вимірів|, дуже різноманітні|всілякі|. Розподіл ряду|лави| систематичних похибок, викликаних|спричиняють| тим або іншим джерелом, відбувається|походить| за своїм, властивим цьому джерелу похибок, закону. Розглянемо|розглядуватимемо| деякі з них:
1. Характеристика постійних систематичних похибок
У всіх результатах вимірів такі похибки мають однакову величину і знак. Класичний приклад|зразок| такої похибки – відхилення стрілки від нульової відмітки перед зважуванням у|біля| вагів із|із| стрілочною індикацією. У практиці геодезичних вимірів|вимірів| це похибки координат і висот опорних точок, похибка визначення місця|місце-милі| нуля|нуль-індикатора| вертикального круга|кола| при тахометричній| зйомці. Підвищуючи точність вимірів|вимірів|, при визначенні опорних точок і ретельніше визначаючи місце|місце-милі| нуля|нуль-індикатора|, можна звести постійні систематичні похибки до величин якими нехтуємо порівняно з випадковими похибками. При точних кутових вимірюваннях|вимірах| визначають елементи відхилення приладу і візирних цілей від центрів знаків і впроваджують відповідні поправки (за центрування|центрування| і редукцію) до результатів вимірів|вимірів|.
2. Характеристика змінних систематичних похибок, залежних
від величини вимірюваного об'єкту і зовнішніх умов вимірів|вимірів|
Розглянемо|розглядуватимемо| приклади|зразки| такого роду похибок (рис. 3.4). Якщо довжина стрічки або рулетки відхиляється від номінального значення на величину δ, то результат вимірювання|виміру| лінії буде викривлений систематичною похибкою
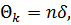(3.2)
де n – кількість відкладень мірного приладу вздовж|вздовж| вимірюваної лінії.
Довжина рулетки
Довжина рулетки
Довжина рулетки
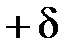
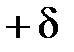
Об'єкт, що вимірюється
Систематична похибка
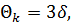
Справжнє
значения
Рис. 3.4 – Ілюстрація систематичних похибок
Для усунення цієї похибки необхідно стрічку або рулетку перед початком роботи прокомпарувати|, визначити величину δ і вводити|запроваджувати| до всіх результатів вимірів|вимірів| поправки, що обчислюються за формулою (3.2). Ця поправка має знак «+»|, якщо δ>0, і знак «-»|, якщо δ<0.
Інший приклад|зразок|. Компарування стрічки або рулетки здійснюється за певної температури t0. Реальні вимірювання|виміри| здійснюють|виробляють| за температури t. Внаслідок цього виникає систематична похибка, зумовлена зміною довжини приладу
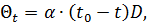(3.3)
де α – коефіцієнт лінійного розширення матеріалу, з|із| якого виготовлений мірний прилад; D – довжина вимірюваної|виміряти| лінії.
Вимірявши|виміряти| температуру t, можна обчислити|обчисляти| величину Θt і ввести|запроваджувати| до результату вимірювання|виміру| відповідну поправку.
3. Характеристика періодичних систематичних похибок
Це інструментальні похибки, зумовлені ексцентриситетом алідади| горизонтального або вертикального круга теодоліта. Вони мають періодичний характер|вдачу| з|із| періодом, що дорівнює 
. Рівняння компенсації цієї похибки має вигляд|вид|
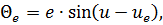(3.4)
де е – лінійний елемент ексцентриситету; ue – результат відліку за лімбом, який відповідає діаметру, що співпадає з|із| елементом е; u – результат довільного відліку за лімбом.
Ексцентриситет алідади| може бути визначений експериментально. За експериментальними|дослідними| даними обчислюється Θe за формулою (3.4) і у разі потреби у виміряні напрями|направлення| вводяться|запроваджують| відповідні поправки.
4. Характеристика однобічно діючих систематичних поправок
Такого роду похибки мають місце:
- внаслідок випадкових відхилень мірного приладу від створу лінії при вимірюванні|вимірі| довжин ліній мірною стрічкою або рулеткою;
- внаслідок випадкових відхилень рейки від вертикального положення|становища| при геометричному нівелюванні.
Якими би не були величини і знак цих відхилень, в тому й іншому випадках вони неминуче збільшують довжину вимірюваної лінії або результат відліку за рейкою. Визначити величину такого роду похибки неможливо. Для послаблення|ослабіння| їх впливу застосовують більш точні методи укладання мірного приладу в створі лінії, в першому випадку, або використовують рейки, забезпечені круглим рівнем, – в другому.
| <== попередня сторінка | | | наступна сторінка ==> |
| Властивості випадкових похибок | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |