
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Основна теорема теорії похибок
У геодезичній практиці переважно використовуються не окремі безпосередньо зміряні величини, а їх функції, тобто непрямі вимірювання. Так, наприклад, нахил лінії визначають як відношення безпосередньо виміряного перевищення і довжини лінії. Довжина лінії, недоступної для безпосереднього вимірювання, обчислюється із розв’язання трикутника, у якого безпосередньо виміряні базисна сторона і горизонтальні кути. Площу земельної ділянки прямокутної форми обчислюють як добуток безпосередньо виміряної довжини і ширини ділянки. Перелік подібних прикладів можна продовжувати. Звідси виникає завдання оцінювання точності функції виміряних величин за відомими стандартами σ або средньоквадратичними похибками m безпосередньо виміряних аргументів. Для розв’язання цього завдання доведена теорема.
Теорема 4.1.Якщо певна безперервна функція, що диференціюється за всіма аргументами
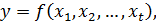 (4.1)
(4.1)
аргументи якої x1, x2,…, xt – незалежні результати безпосередніх вимірів певних величин X1, X2,…, Xt, виконаних в умовах, що характеризуються стандартами σ1, σ2,…, σt, то стандарт цієї функції буде дорівнювати
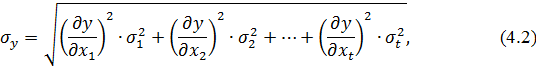
де 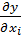 – частинні похідні функції (4.1) за змінними x1, x2,…, xt ,
– частинні похідні функції (4.1) за змінними x1, x2,…, xt , 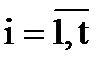
Доказ. З курсу математичного аналізу відомо, що повний диференціал функції (4.1) дорівнює
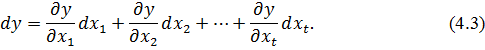
n-я серія
вимірювань
|
2-я серія
вимірювань
|
1-я серія
вимірювань
|
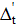
|
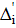
|
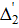
|
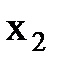
|
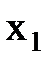
|
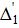
|
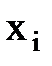
|
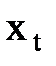
|
| … |
| … |
| … |
| … |
| … |
| … |
| … |

|
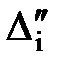
|
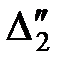
|
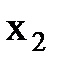
|
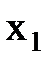
|
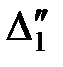
|
| … |
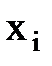
|
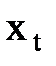
|
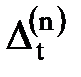
|
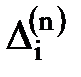
|

|
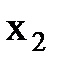
|
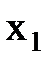
|

|
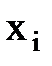
|
|
Рис. 4.1 – Графічна інтерпретація величин вимірів і їх похибок
Припустимо, що величини x1, x2,…, xt виміряні n разів. При цьому результати вимірів містять випадкові похибки, які позначимо:
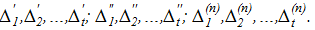
Наочно|наглядний| в графічній формі величини вимірів|вимірів| і їх похибки, ілюструються рис. 4.1.
Вважаючи, що похибки Δі є приростами величин хі (малими величинами), то на підставі запису повного диференціала (4.3) можна записати систему рівнянь у частинних похідних, де кожне з рівнянь характеризує зміну похибок у серії вимірів величин x1, x2,…, xt

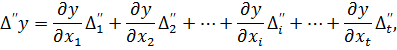
… (4.4)
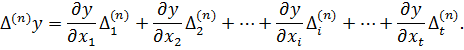
Відзначимо, що кожен елемент 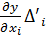 ,
, 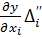 ,…,
,…, 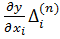 ,
, 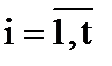 системи рівнянь має константу
системи рівнянь має константу 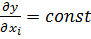 . Для того, щоб точно оцінити функції виміряних величин y = f (x1, x2,…, xt) з використанням стандарту σ або середньоквадратичної похибки m (див. формулу 2.14 і 3.6) необхідно здійснити наступні перетворення з системою рівнянь (4.4). Звести у квадрат праві та ліві частини кожного з рівнянь. Отримаємо
. Для того, щоб точно оцінити функції виміряних величин y = f (x1, x2,…, xt) з використанням стандарту σ або середньоквадратичної похибки m (див. формулу 2.14 і 3.6) необхідно здійснити наступні перетворення з системою рівнянь (4.4). Звести у квадрат праві та ліві частини кожного з рівнянь. Отримаємо
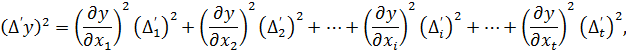

… (4.5)
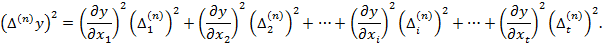
Тепер кожне з рівнянь є сумою квадратів. Для того, щоб привести праві частини рівнянь до вигляду відомих формул скороченого множення многочленів  додамо до кожного рівняння суми добутків, що складаються з двох пар у кожному многочлені. Отримаємо
додамо до кожного рівняння суми добутків, що складаються з двох пар у кожному многочлені. Отримаємо
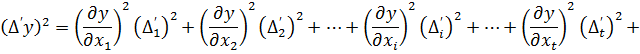

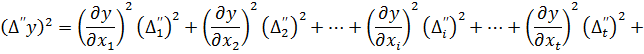
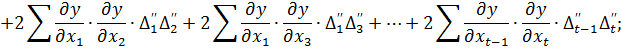
… (4.6)
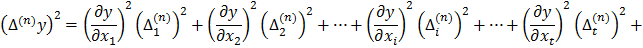

Підсумуємо змінні лівої і правої частини|частки| отриманих|одержувати| многочленів і запишемо їх в символах Гаусса К.Ф.
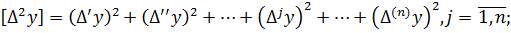
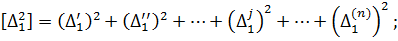
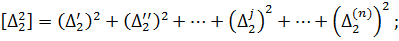
… (4.7)
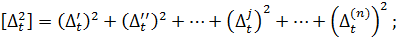
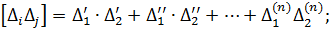
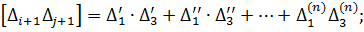
…
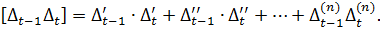
Розділимо отримані суми на n і запишемо остаточний вираз, що враховує всі змінні (похибки Δi) системи рівнянь (4.4)
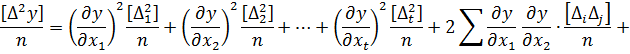
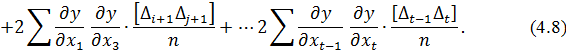
Припускаючи, що n → ∞, знайдемо межі лівої і правої частини отриманого виразу. На основі властивості незалежності (2.13) маємо наступне:

Враховуючи властивість розсіювання (2.14) для правої і лівої частини|частки| рівняння (4.8) справедливо записати


Спростимо вираз (4.8), відкинувши подвійні суми  , оскільки вираз (4.9) їх перетворює на нуль, і, застосовуючи до його лівої частини граничне значення формули (4.10), а до правої частини – граничні значення формули (4.11) і добувши з них квадратний корінь, отримаємо вираз (4.2), що і потрібно було довести.
, оскільки вираз (4.9) їх перетворює на нуль, і, застосовуючи до його лівої частини граничне значення формули (4.10), а до правої частини – граничні значення формули (4.11) і добувши з них квадратний корінь, отримаємо вираз (4.2), що і потрібно було довести.
4.2. Застосування|вживання| основної теореми для розрахунку гранично
допустимої нев'язки|нев'язки|
Розрахунок гранично допустимої кутової нев'язки|нев'язки| теодолитного| ходу
Вважатимемо, що всі кути виміряні теодолітом технічного класу точності в умовах, що характеризуються стандартом σβ = 30'' і є равноточними. Відомо, що кутова нев'язка обчислюється за формулою

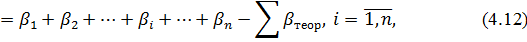
Де β1, β2,…, βn – незалежні змінні величини; ∑βтеор – для цього ходу є величиною постійною.
Знайдемо частинні похідні функції (4.12) за змінними βi:
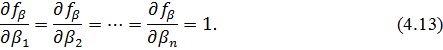
Скористаємося формулою (4.2), що характеризує стандарт цієї функції, і, враховуючи отриману|одержувати| формулу (4.13), а також враховуючи обмеження, що усі виміри|виміри| рівноточні,| можна записати
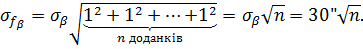
Для розрахунку граничної нев'язки скористаємося виразом (3.10). Тоді для нашого випадку, де σβ = 30'' гранично допустима кутова нев'язка теодолітного ходу розраховується за формулою:

Розрахунок гранично допустимої кутової нев'язки|нев'язки| нівелірного|нівелір| ходу
Припустимо, що нівелірний хід довжиною L км. прокладений на рівнинній місцевості, де на кожний кілометр ходу припадає приблизно однакова кількість станцій за середньої відстані 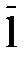 між рейками на одній станції. Риска над буквою l позначає середнє значення відстані. Отже, кількість усіх станцій, які припадають на довжину ходу буде близьким до величини
між рейками на одній станції. Риска над буквою l позначає середнє значення відстані. Отже, кількість усіх станцій, які припадають на довжину ходу буде близьким до величини

Крім того, вимірювання на станції вважатимемо за равноточні, виконані в умовах, що характеризуються стандартом σст.
Нев'язку|нев'язку| нівелірного|нівелір| ходу розраховують за формулою
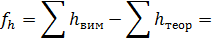
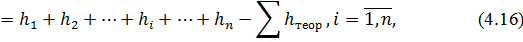
де h1, h2,…, hn як і у виразі (4.12) незалежні змінні ∑hтеор – постійна величина.
Знаходимо частинні похідні функції (4.16) за змінними hi
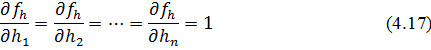
За аналогією з розрахунком припустимої кутової нев'язки|нев'язки| теодолітного| ходу для розрахунку припустимої нев'язки|нев'язки| нівелірного|нівелір| ходу запишемо
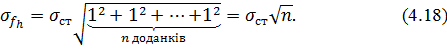
Для розрахунку граничної нев'язки|нев'язки| нівелірного|нівелір| ходу скористаємося формулою (3.11). Тоді, враховуючи вираз|вираження| (4.15), отримаємо

Величини стандарту σст для кожного класу нівелювання встановлені нормативними документами, тобто є постійними. Спростимо формулу (4.19), ввівши наступне позначення
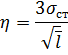
і підставимо його у вираз|вираження| (4.19), отримаємо|одержуватимемо| відому з|із| геодезії формулу

де η – коефіцієнт, залежний від класу нівелювання. Для IV класу η = 20 мм, для технічного нівелювання η = 50 мм.
4.3. Апостеріорна оцінка точності функцій виміряних|виміряти| величин
На практиці при апостеріорній оцінці точності функції y = f (x1, x2,…, xt) виміряних величин X1, X2,…, Xt невідомі стандарти σ1, σ2,…, σt у формулі (4.2) замінюють середніми квадратичними похибками m1, m2,…, mt. Тоді
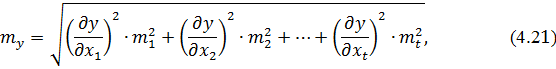
Розрахунки виконуються в наступній|слідуючій| послідовності:
1. Функцію (4.1) записують|занотовують| в явному вигляді|виді|;
2. Знаходять|находять| частинні похідні цієї функції за всіма незалежними змінними (похідні найпоширеніших функцій приведені в додатку В);
3. Підставляють частинні похідні і середні квадратичні похибки до формули (4.21);
4. Виконують необхідні математичні перетворення і отримують|одержують| остаточний результат.
Приклад 4.1. За відомими результатами вимірів: перевищенням hAB=12,6м, довжиною проекції лінії АВ dAB= 468 м і оцінками їх точності (середніми квадратичними похибками) mh = 0,1 м і md = 0,5 м відповідно, необхідно знайти середню квадратичну похибку ухилу лінії АВ, схематично зображеної на рис. 4.2.
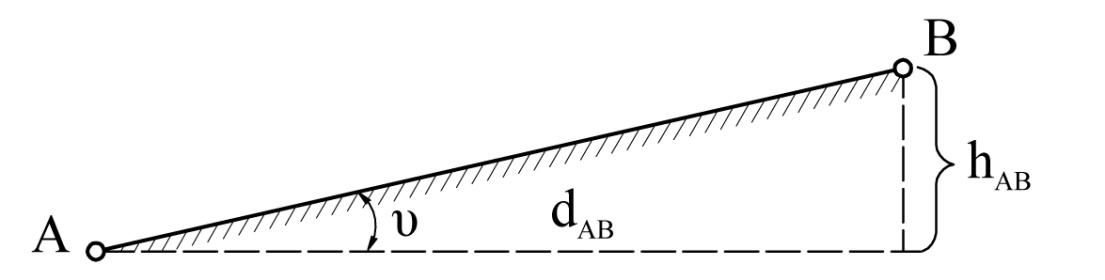
Рис. 4.2 – Графічна інтерпретація ухилу
Рішення. Використовуючи рекомендовану послідовність оцінювання точності виміряних величин, задамо в явному вигляді функцію виміру ухилу відому з геодезії i = tgυ, де 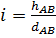 . Підставляючи до формули чисельні значення, отримаємо
. Підставляючи до формули чисельні значення, отримаємо 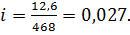
Другим кроком у розв’язанні поставленої задачі є знаходження частинних похідних функції 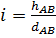 за змінними hAB і dAB. Продиференціюємо цю функцію спочатку за змінною hAB, зафіксувавши змінну dAB, отримаємо
за змінними hAB і dAB. Продиференціюємо цю функцію спочатку за змінною hAB, зафіксувавши змінну dAB, отримаємо 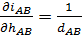 , а після того за змінною dAB зафіксувавши hAB,
, а після того за змінною dAB зафіксувавши hAB, 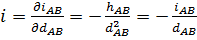 .
.
На третьому кроці розв’язання поставленої задачі скористаємося формулою (4.21), перетворюючи її на формулу для обчислення середньоквадратичної |підрахунку|| похибки ухилу|уклону|. Формула (4.21) прийме вигляд:
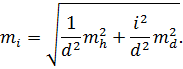
На четвертому кроці розв’язання задачі до отриманої формули підставимо чисельні значення і зробимо відповідні обчислення, отримаємо mi ≈ 0,0002.
Таким чином, завдання знаходження середньої квадратичної похибки ухилу за заданими апостеріорними оцінками розв’язане. Мала величина mi свідчить про точне визначення ухилу заданої лінії.
Приклад 4.2. На топографічній карті виміряні прямокутні координати X і Y точок 1 і 2 (рис.4.3). Середні квадратичні похибки визначення координат точок дорівнюють 
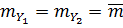 . За координатами обчислені довжина d і дирекційний кут α лінії 1-2.
. За координатами обчислені довжина d і дирекційний кут α лінії 1-2.
Необхідно визначити середні квадратичні похибки md і mα.

|
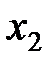
|
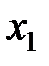
|

|
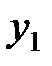
|
| x |
| y |
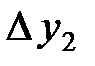
|
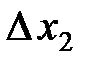
|
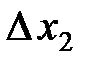 , , 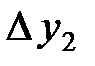 - похибка одного вимірювання|виміру| координат точки 2 - похибка одного вимірювання|виміру| координат точки 2
|
Рис. 4.3 – Графічна інтерпретація багатократного вимірювання
координат двох точок
Розв’язання.З умов завдання видно, що обчислення довжини лінії d залежить від результатів вимірювання координат точок 1 і 2. Отже, змінними в цьому випадку є координати точок 1 (X1; Y1) та 2 (X2; Y2),
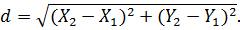
Візьмемо частинні похідні від d за змінними X1 і X2
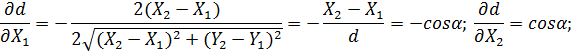
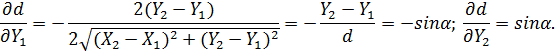
Перетворимо вираз|вираження| (4.21) з урахуванням|з врахуванням| результатів диференціювання і рівності середніх квадратичних| похибок, заданих в умові завдання.|задачі| Запишемо
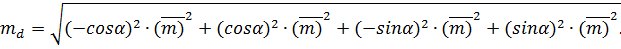
Перетворимо отриманий вираз і винесемо 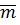 за знак радикала
за знак радикала
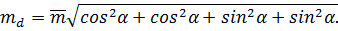
Спростимо підкорінний вираз, використовуючи відому тригонометричну формулу cos2α + sin2α = 1. Тоді 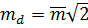 . Отримана формула для обчислення середньої квадратичної похибки вимірювання md довжини лінії d.
. Отримана формула для обчислення середньої квадратичної похибки вимірювання md довжини лінії d.
Для обчислення середньої квадратичної похибки mα скористаємося тригонометричною функцією, яка пов'язує дирекційний кут із результатами вимірів координат точок 1 і 2. Така функція очевидна (рис.4.3) і має наступний вигляд:
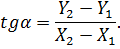
Для зручності подальших|дальших| перетворень прологарифмуємо отриману|одержувати| функцію:
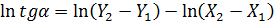 .
.
Обчислимо|обчислятимемо| похідну лівої частини|частки|, отриманого|одержувати| рівняння:
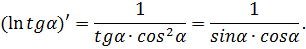
Знайдемо частинні похідні від α за змінними X1, X2
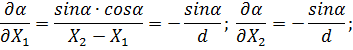
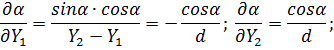
Проводячи|виробляти| перетворення з використанням формули (4.21) і спрощення аналогічні попередньому прикладу,|зразку| отримаємо|одержуватимемо|
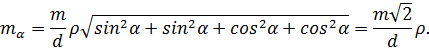
Тут ρ – коефіцієнт переходу від міри радіану до градусного вимірювання ρ=3438 (кількість минут в одному радіані).
Таким чином, отримано дві прості формули за допомогою, яких можна обчислити значення середньої квадратичної похибки md вимірювання довжини лінії d, а також значення середньої квадратичної похибки mα дирекційного кута α. Причому похибка дирекційного кута, обчисленого за координатами, обернено пропорційна довжині лінії.
Приклад 4.3. Виміряні довжина а = 59,85 м і b = 20,10 м земельної ділянки прямокутної форми з середньою квадратичною відносною похибкою 1:2000. (рис. 4.4).
| Δa, Δb – похибки вимірювання сторін аі b, які зумовлюють обчислення |
| Δb |
| Δa |
| b |
| a |
| 1:2000 |
Рис. 4.4 – Геометрична інтерпретація умов розв’язання задачі
Необхідно знайти площу|майдан| ділянки і середньоквадратичну| відносну похибку визначення площі|майдану|.
Розв’язання.Запишемо формулу обчислення площі земельної ділянки і обчислимо її за відомими даними.
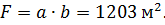
З рис. 4.4 видно, що зміряні величини аі bє змінними і від точності їх вимірювання залежить точність обчислення площі земельної ділянки.
З метою спрощення обчислень прологарифмуємо отриманий вираз 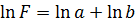 і знайдемо повний диференціал функції
і знайдемо повний диференціал функції
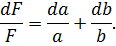
Замінивши в отриманому|одержувати| виразі|вираженні| диференціали середніми квадратичними | похибками, враховуючи формулу (4.21) отримаємо
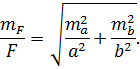
 |одержуватимемо|За умовами завдання|задачі|
|одержуватимемо|За умовами завдання|задачі|
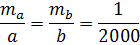
Підставимо отримане значення до формулу обчислення|підрахунку| середньої квадратичної | похибки, і знайдемо

За необхідності у процесі аналізу точності вимірів|вимірів| можна перейти до абсолютних похибок
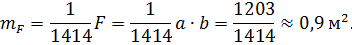
Таким чином, знайдена площа|майдан| земельної ділянки і показники точності проведених вимірів|вимірів| (середні квадратичні| похибки вимірів|вимірів|). Отримані|одержувати| показники можуть бути покращені за рахунок вимірювання земельної|виміру| ділянки точнішими приладами, а також збільшенням кількості вимірів|вимірів|.
Розглянуті вище приклади приведуть до поняття «Надійність апостеріорної оцінки точності вимірів». Оцінка такої надійності пов'язана з певними труднощами, які зумовлені застосуванням спеціальної технології вимірів і використанням основної теореми теорії похибок. Технологія передбачає вимірювання кожної незалежної змінної декількома серіями і для кожної серії обчислення середньої квадратичної похибки m1, m2,…, mi,…, mt а потім обчислення середньої квадратичної похибки всіх серій вимірів. Продиференціюємо функцію (4.21) за змінними 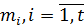 . У результаті отримаємо
. У результаті отримаємо
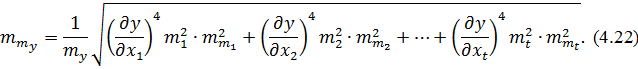
Використовуючи раніше отриманий вираз (3.14) 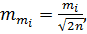 підставимо його до виразу (4.22). Отримаємо залежність величини
підставимо його до виразу (4.22). Отримаємо залежність величини 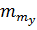 від кількості вимірів
від кількості вимірів
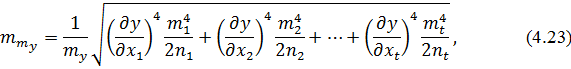
де 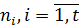 – кількість вимірів в i-й серії.
– кількість вимірів в i-й серії.
Таким чином, очевидно, що підвищення надійності апостеріорної оцінки точності вимірів|вимірів|, пов'язано з додатковими трудовими витратами з серійного вимірювання|виміру| кожного параметра (незалежною змінною).
| <== попередня сторінка | | | наступна сторінка ==> |
| ОЦІНКА ТОЧНОСТІ ФУНКЦІЙ | | | Проста арифметична середина і її властивості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |