
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Проста арифметична середина і її властивості
Якщо 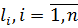 – ряд|лава| незалежних результатів рівноточних| вимірів|вимірів| однієї і тієї ж величини Х, то за якнайкраще|щонайкраще| наближення до її дійсного значення зазвичай|звично| приймають просту арифметичну середину, яка обчислюється за елементарною формулою
– ряд|лава| незалежних результатів рівноточних| вимірів|вимірів| однієї і тієї ж величини Х, то за якнайкраще|щонайкраще| наближення до її дійсного значення зазвичай|звично| приймають просту арифметичну середину, яка обчислюється за елементарною формулою

де n – кількість рівноточних| вимірів|вимірів|, а квадратні дужки означають суму результатів вимірів|вимірів| у символах К.Ф. Гаусса.
Такі обчислення|підрахунки| є|з'являються| правомірними, тому що вони враховують властивості арифметичної середини, які розглянемо|розглядуватимемо| нижче.
Властивості простої арифметичної середини
Властивість 1. Якщо результати вимірів вільні від систематичних похибок, то проста арифметична середина цих результатів при збільшенні кількості вимірів в межі наближається до дійсного значення вимірюваної величини, тобто

Враховуючи властивості систематичних похибок можна записати
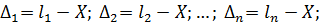
Використовуючи результати доведення основної теореми теорії похибок, підсумуємо праві і ліві частини|частки| отриманих|одержувати| виразів і розділимо їх на n (див. доведення теореми в п.п. 4.1). Отримаємо
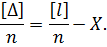
 |одержуватимемо|Використовуючи вираз|вираження| (5.1), очевидно, що отриману|одержувати| рівність можна записати у вигляді|виді|
|одержуватимемо|Використовуючи вираз|вираження| (5.1), очевидно, що отриману|одержувати| рівність можна записати у вигляді|виді|
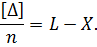
За n→∞ ліва частина цього виразу на підставі властивості компенсації випадкових похибок (2.11) наближається до нуля. Права його частина так само наближається до нуля, що доводить справедливість виразу (5.2).
Отже, проста арифметична середина L є|з'являється| спроможним оцінити величину Х.
Властивість 2. Арифметична середина незалежних рівноточних результатів вимірів має стандарт в 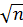 раз менший стандарту σ цих вимірів.
раз менший стандарту σ цих вимірів.
Представимо|уявлятимемо| вираз|вираження| (5.1) у вигляді
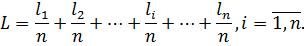
 |виді|Скориставшись процедурами доведення основної теореми теорії похибок в отриманому виразі, візьмемо частинні похідні за кожною змінною li
|виді|Скориставшись процедурами доведення основної теореми теорії похибок в отриманому виразі, візьмемо частинні похідні за кожною змінною li

тоді формула (4.2) набуває вигляду:
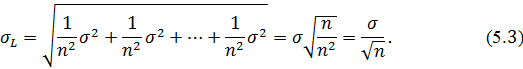
Наочно арифметичну середину рівноточних результатів вимірів можна представити, зобразивши графічно (рис. 5.1) ділянки розсіювання похибок Δ і ΔL.
| Δ |
| -3σ |
| 3σ |
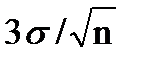
|
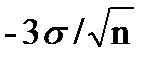
|
| L |
| ΔL |
Рис. 5.1 – Ілюстрація розподілу похибок відносно арифметичної
середини рівноточних| вимірів|вимірів|
Ділянка можливого розсіювання похибок ΔL буде тим вужча, чим більша кількість вимірів n. У зв'язку з цим виникає питання, чи є збільшення кількості вимірів ефективною процедурою підвищення їх точності? При n ≤ 10 на це питання можна відповісти позитивно. Але за збільшення кількості вимірів n точність вимірів змінюватиметься повільніше, ніж збільшення n. Так, для підвищення точності в 4 рази буде потрібно 16 вимірів, в 5 разів – 25, в 6 разів – 36, у 10 разів – 100 вимірів.
Крім того, завжди залишаються малі похибки порівняно з випадковими систематичними похибками, які не вдалося цілком виключити. Досягши деякого n вони стають переважаючими|пануючими| у величині L і перешкоджатимуть подальшому|дальшому| підвищенню точності. Таким чином, збільшення кількості вимірів,|вимірів| з одного боку, збільшує їх точність|вимірів|, з іншого боку, велика кількість вимірів|вимірів| вимагає великих витрат часу|затрат|, що може призвести до зміни умов і неминучого порушення рівноточних| вимірів|вимірів|.
Властивість 3. Якщо арифметична середина, отримана з результатів вимірів вільних від систематичних похибок, то і сама вона не містить систематичної похибки.
Припустимо зворотне, тобто результати вимірів містять систематичні похибки θ1, θ2,…, θi,…, θn. Тоді на підставі (2.9) можна записати:

Склавши праві і ліві частини|частки| отриманих|одержувати| рівнянь між собою і розділивши їх на n, отримаємо
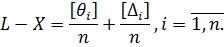
 |одержуватимемо|Права частина отриманого рівняння складається з двох доданків, що є систематичною і випадковою похибками арифметичної середини. Звідси випливає, що якщо θ1= θ2=…= θn=0, то і
|одержуватимемо|Права частина отриманого рівняння складається з двох доданків, що є систематичною і випадковою похибками арифметичної середини. Звідси випливає, що якщо θ1= θ2=…= θn=0, то і 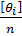 дорівнюватиме 0, що і доводить сформульовану вище властивість.
дорівнюватиме 0, що і доводить сформульовану вище властивість.
Таким чином, за відсутності систематичних похибок арифметична середина L є не тільки спроможним, але і незміщеним оцінюванням величини Х. Таку оцінку в геодезії називають найймовірнішим значеннямвимірюваної величини.
За наявності систематичних похибок арифметична середина також міститиме|утримуватиме| систематичну похибку
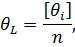
а тому не має властивостей 1 і 3. У цьому випадку арифметична середина L хоча і дасть якнайкраще|щонайкраще| з|із| можливих наближень до Х, але|та| не буде її найймовірнішим| значенням.
Раніше було відзначено, що вплив випадкових похибок можна ослабити належною математичною обробкою. Такого роду обробку називають зрівнюванням результатів вимірів.
Результати вимірів зрівнюють шляхом введення в обчислення поправок. Під точною поправкою 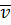 розумітимемо величину, додавши яку до результатів вимірювання l отримаємо значення Х, тобто
розумітимемо величину, додавши яку до результатів вимірювання l отримаємо значення Х, тобто

Перетворимо отриманий|одержувати| вираз|вираження| і представимо його у вигляді|виді|:
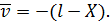
З отриманого співвідношення випливає, що точна поправка 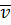 за абсолютною величиною дорівнює похибці, але протилежна їй за знаком. Відзначимо, що знайти точні поправки у більшості випадків геодезичної практики не є можливим, тому доводиться використовувати наближені поправки. Під наближеною поправкою
за абсолютною величиною дорівнює похибці, але протилежна їй за знаком. Відзначимо, що знайти точні поправки у більшості випадків геодезичної практики не є можливим, тому доводиться використовувати наближені поправки. Під наближеною поправкою 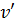 розумітимемо величину, додавши яку до результату вимірювання l отримаємо деяке наближене до Х значення y, тобто
розумітимемо величину, додавши яку до результату вимірювання l отримаємо деяке наближене до Х значення y, тобто

Додавши наближену поправку до результату li отримаємо найймовірніше значення L, яке називається найймовірнішою поправкою, тобто

Графічна інтерпретація розглянутих|розглядувати| вище поправок ілюструється рис. 5.2 і рис. 5.3.
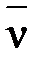
|
| Х |
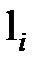
|
| Точна поправка, отримана|обчисляти| математичною обробкою результатів вимірювань|вимірів| |
Рис. 5.2 – Ілюстрація зрівнювання результатів вимірів точною поправкою
Наступні|такі| властивості (властивість 4 і 5) арифметичної середини пов'язані з найймовірнішими| поправками.
Властивість 4.Якщо за ймовірніше значення вимірюваної величини прийнята арифметична середина, то сума найймовірніших поправок дорівнює нулю, тобто

На підставі|основі| (5.6) запишемо наступну|таку| систему лінійних рівнянь

Отримані|одержувати| лінійні рівняння підсумуємо і запишемо їх, використовуючи символіку К.Ф. Гаусса

Порівнюючи рівняння (5.9) з перетвореним рівнянням простої арифметичної середини (5.1), а саме  очевидно, що
очевидно, що 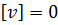 .
.
Властивість 5.Сума квадратів найймовірніших поправок, отриманих з арифметичної середини, завжди менша суми квадратів наближених поправок, отриманих для будь-якої іншої функції тих же результатів вимірів.
На підставі виразу|вираження| (5.5) і рис.5.3 запишемо систему лінійних рівнянь.
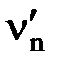
|
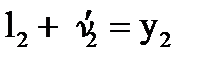
|
| … |
| … |
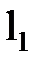
|
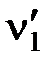
|
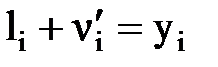
|
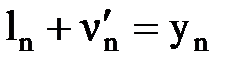
|
| Величина, що вимірюється |
| Арифметичне середнє поправок |
| L |
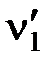
|
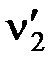
|
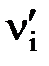
|
| Найймовірніша поправка |
Рис. 5.3 – Ілюстрація зрівнювання результатів вимірів
| найймовірнішою поправкою
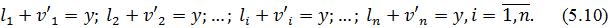
Віднімемо від|із| кожного рівняння отриманої|одержувати| системи лінійних рівнянь (5.10) рівняння системи (5.8) і, зробивши відповідні перетворення, отримаємо|одержуватимемо|:
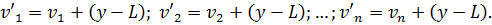
Піднесемо до квадрата праві і ліві частини|частки| отриманих|одержувати| рівнянь
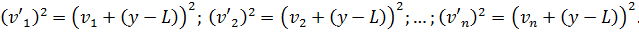
Скориставшись формулами скороченого множення многочленів для квадратів, отримаємо

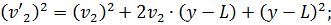 |одержуватимемо|
|одержуватимемо|
...
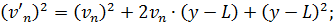
Підсумуємо отримані|одержувати| вирази і запишемо їх в символах К.Ф. Гаусса
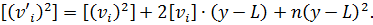
У правій частині отриманої рівності середній доданок дорівнює нулю внаслідок того, що 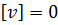 (див. формулу 5.7). Тому
(див. формулу 5.7). Тому
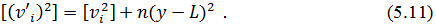
Звідси випливає нерівність 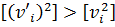 або
або  яка і доводить сформульовану вище властивість.
яка і доводить сформульовану вище властивість.
Таким чином, розглянуті|розглядувати| властивості простої арифметичної середини є однією з основних характеристик оцінювання точності рівноточних| геодезичних вимірів|вимірів|. Знання властивостей простої арифметичної середини дозволяє правильно організувати математичну обробку рівноточних| геодезичних вимірів|вимірів|.
5.2. Формула розрахунку емпіричної середньої квадратичної| похибки
У п.3 розглянуті|розглядувати| кількісні критерії і чисельні приклади|зразки| апостеріорної оцінки точності ряду|лави| незалежних рівноточних| вимірів|вимірів| однієї величини за дійсними похибками. Цей спосіб є|з'являється|, безумовно, ефективним тільки|лише| тоді, коли у процесі вимірів|вимірів| поруч з|поряд з| результатами вимірів|вимірів| отримують|одержувати| їх дійсні похибки. Проте|однак| у багатьох випадках геодезичної практики дійсні похибки залишаються невідомими. Тому виникає необхідність апостеріорної оцінки точності вимірів|вимірів| за їх результатами.
Наведемо доказ теореми.
Теорема 5.1. Якщо l1, l2,…, ln – результати незалежних рівноточних вимірів, вільних від змінних систематичних похибок, то величина

де v – найймовірніші поправки, є спроможне і незміщене наближення до квадрата стандарту, тобто дисперсії σ2 випадкових оцінок вимірюваної величини.
Результати вимірів|вимірів| представимо|уявлятимемо| у вигляді|виді|:
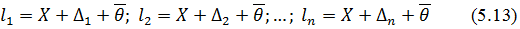
де 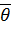 – постійна систематична похибка; Δi – випадкова похибка, Х – дійсне значення вимірюваної величини.
– постійна систематична похибка; Δi – випадкова похибка, Х – дійсне значення вимірюваної величини.
Оскільки|тому що| постійна систематична похибка враховується при обчисленні|підрахунку| арифметичної середини, то справедлива рівність

де ΔL – дійсна випадкова похибка арифметичної середини.
Віднімемо з отриманого виразу по черзі кожне із системи рівнянь (5.13) і, зважаючи на систему лінійних рівнянь (5.8) 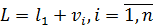 отримаємо наступне|одержуватимемо|:
отримаємо наступне|одержуватимемо|: 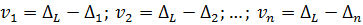 . Представимо|уявлятимемо| ці вирази у наступному вигляді|виді|:
. Представимо|уявлятимемо| ці вирази у наступному вигляді|виді|: 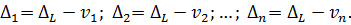
Піднесемо, ліві і праві частини|частки| до квадрата, а результати підсумуємо наступним чином:
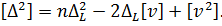
Підставивши в отриманий вираз формулу (5.7), тобто 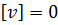 отримаємо:
отримаємо:

Перетворюючи цей вираз отримаємо: 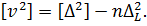 У правій частині винесемо за дужку n і поділимо обидві частини рівняння на n-1. У результаті отримаємо
У правій частині винесемо за дужку n і поділимо обидві частини рівняння на n-1. У результаті отримаємо
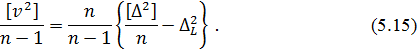
Спочатку доведемо, що права частина отриманого виразу є спроможною оцінкою дисперсії. Для цього перейдемо до межі при n→∞. Скористаємося методами математичного аналізу, зокрема правилом Лопіталя, при розкритті невизначеності  яке є складовою
яке є складовою 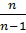 правої частини рівняння (5.15), перетворює на одиницю
правої частини рівняння (5.15), перетворює на одиницю
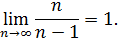
Друга складова правої частини рівняння (5.15) через першу властивість простої арифметичної середини при n→∞ наближається до нуля
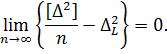
Тоді через властивість розсіювання (2.14) випадкових похибок ліву частину рівняння (5.15) справедливо прирівняти до значення дисперсії σ2
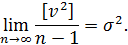
Таким чином, перша частина|частка| теореми доведена.
Для доказу другої частини|частки| теореми припустимо|передбачатимемо|, що виконано t серій незалежних рівноточних| вимірів
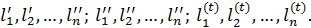 |вимірів|
|вимірів|
Для кожної серії вимірів запишемо формулу для розрахунку середньої квадратичної похибки 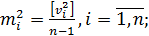
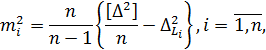
де Δ – похибка кожного вимірювання в серії, а 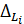 – похибка i-ї серії вимірів. Підсумуємо отримані вирази і отримаємо формулу
– похибка i-ї серії вимірів. Підсумуємо отримані вирази і отримаємо формулу
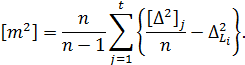
Особливість запису отриманого виразу полягає в тому, що він записаний на змішаній математичній мові, тобто з використанням формального представлення символу суми «[ ]» К.Ф.Гаусса, а також загальноприйнятого в математиці символу суми «∑».
Розділимо почленно все на t і переходячи до межі при t→∞ матимемо
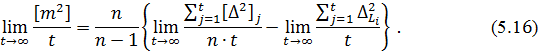
Розглянемо границі у фігурних дужках виразу (5.16). Перша границя згідно з властивості розсіювання дорівнює σ2, оскільки в чисельнику стоїть сума квадратів випадкових похибок, а в знаменнику – їх кількість. Друга границя є границею суми квадратів випадкових похибок арифметичної середини , що ділиться на їх кількість, що згідно властивості розсіювання дорівнює  і, зважаючи на другу властивість арифметичної середини (5.3), отримаємо
і, зважаючи на другу властивість арифметичної середини (5.3), отримаємо 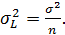
Зробивши відповідні підстановки, знаходимо
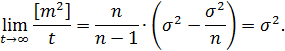
|находимо|Отже, оцінка (5.11) є незміщеною. Таким чином, отримано незміщене наближення до стандарту σ, що і потрібно було довести.
Зберігаючи в (5.11) те ж позначення середньої квадратичної похибки m, як і в (3.6), щоб їх якось розрізняти, наближення (5.11) називатимемо емпіричною середньоквадратичною похибкою.
5.3. Послідовність математичної обробки ряду|лави| рівноточних|
вимірів|вимірів| однієї і тієї ж величини
Перш ніж безпосередньо підійти до розгляду послідовності математичної обробки рівноточних| вимірів|вимірів| виведемо декілька контрольних і допоміжних формул.
Для обчислення|підрахунку| простої арифметичної середини на практиці замість формули (5.1) зручно використовувати формулу, що має вигляд

|вид|де L0 – так званий «умовний нуль», тобто доцільно вибране наближене значення, щоб різниці

були малими величинами, δ – деяка погрішність li вимірювання. Графічна інтерпретація пошуку арифметичної середини з використанням «умовного нуля» ілюструється рис.5.4.
| δ2 |
| … |
| … |
| … |
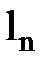
|
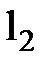
|
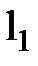
|

|
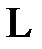
|
| Величина, яку вимірюють |
| δ1 |
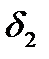
|
| δn |

|
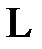
|
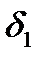
|
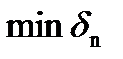
|
Евристична процедура пошуку 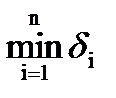
|
| Арифметична |
| середина |
Рис. 5.4 – Ілюстрація знаходження простої арифметичної середини
з використанням «умовного нуля|нуль-індикатора|»
Дійсно, відповідно до (5.17) і (5.18) можна записати
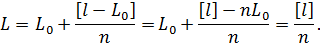
У результаті отримана|одержувати| формула для обчислення|підрахунку| простої арифметичної середини (5.1). Далі для обчислення|підрахунку| за формулою (5.11) емпіричної середньої квадратичної| похибки необхідно спочатку за перетвореною формулою (5.8) обчислити|обчисляти| найймовірніші| поправки
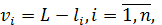
Теоретичною перевіркою правильності обчислення арифметичної середини з використанням «умовного нуля» вимірів може служити четверта властивість арифметичної середини. Проте практика показує, що при обчисленні суми найймовірніших поправок за формулою (5.7) процедура округлення отриманих результатів дає зміщене значення L', що відрізняється від значення L на малу величину β, тобто

і зміщені поправки, також відрізняються від найймовірніших поправок на величину β.

Вищесказане проілюструємо рис. 5.5.
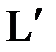
|
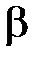
|
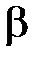
|
| Величина, яку вимірюють |
| Округлення |
| Проста арифметична середина L |
| Зміщене значення вимірюваної величини |
Рис. 5.5 – Ілюстрація зсуву вимірюваної величини за рахунок округлення
найймовірніших| поправок
Підсумуємо всі від 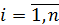 вирази (5.20) і отримаємо наступний формальний запис:
вирази (5.20) і отримаємо наступний формальний запис:
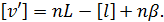
Спираючись|обпиратися| на перетворення, які зроблені при доведенні теореми
(див. п.п. 5.2) можна записати

Відповідно до п'ятої властивості арифметичної середини сума наближених поправок виміряної величини [v'] більше суми найймовірніших поправок [v]. Формально можна записати [v'] > [v].
Для знаходження незміщеного значення вимірюваної величини скористаємося виразом (5.11), який отриманий при обґрунтуванні п'ятої властивості простої арифметичної середини (див. п.п. 5.1). Замінимо в цьому виразі yна L':
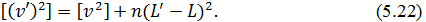
Прості перетворення формул (5.19) і (5.21) дозволяють записати рівність
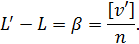
Підставляючи отримані|одержувати| вирази до формули (5.22) отримаємо наступне:

Отримана|одержувати| сума квадратів найймовірніших| поправок вимірюваної величини дорівнює різниці суми квадратів наближеної поправки і середньої величини цих же поправок. Для перевірки правильності математичних побудов знову скористаємося формулою (5.11), замінивши в ній v' на δl, а уна L0, враховуючи при цьому, що 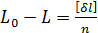 отримаємо
отримаємо

Порівнюючи праві частини|частки| виразів (5.23) і (5.24) видно|показний|, що вони мають один і той же фізичний сенс. Оцінимо|оцінюватимемо| надійність обчислень|підрахунків| зроблених за формулою (5.12), оскільки|тому що| емпірична середня квадратична| похибка є|з'являється| величиною наближеною. Таку оцінку можна зробити, використовуючи формулу

Для визначення середньої квадратичної похибки арифметичної середини L скористаємося обґрунтуванням другої властивості простої арифметичної середини, а саме формулою (5.3). Замінимо в ній невідомі стандарти σ і σL середніми квадратичними похибками m і М, і отримаємо

На підставі отриманих|одержувати| формул (5.25) і (5.26) надійність | величини М|м-коду| можна оцінити|оцінювати|, використовуючи формулу

Розглянуті|розглядувати| вище математичні побудови|шикування| призводять|призводять| до наступної|такої| послідовності математичних процедур з обробки ряду рівноточних|лави| | вимірів|вимірів| однієї і тієї ж величини.
Процедура 1. Евристична процедура з знаходження умовного нуля L0.
Процедура 2. Процедура обчислення арифметичної середини, яка полягає в округленні отриманих результатів і визначенні величини зсуву β за формулою (5.19).
Процедура 3. Обчислення зсуву, яка полягає в округленні найймовірніших поправок v' і їх підсумовування.
Процедура 4. Контрольна перевірка правильності виконаних обчислень. Перевіряється співвідношення величини суми найймовірніших поправок ([v']), отриманих процедурою 4, і добуток кількості вимірів на величину зсуву nβ. Якщо існує нерівність [v'] < nβ, то обчислення виконані правильно.
Процедура 5. Обчислення значень (δli)2 і (vi')2 для кожного вимірювання 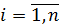 і знаходження їх сум.
і знаходження їх сум.
Процедура 6. Обчислення емпіричної середньої квадратичної похибки m за формулою (5.12), спочатку на основі результатів обчислення [v2], отриманих за формулою (5.23), а потім на основі результатів обчислення тієї ж величини за формулою (5.24). Обидва результати повинні збігтися в межах точності вимірів.
Процедура 7. Оцінювання надійності обчислення наближеного значення емпіричної середньої квадратичної похибки результатів вимірів за формулою (5.25).
Процедура 8. Обчислення середньої квадратичної похибки простої арифметичної середини вимірюваної величини L за формулою (5.26).
Процедура 9. Оцінка надійності отриманих результатів вимірювання здійснюється за формулою (5.27).
Використовуючи наведені вище процедури розглянемо|розглядуватимемо| приклад|зразок| математичної обробки ряду|лави| незалежних рівноточних| вимірів|вимірів| величини горизонтального кута|рогу|, зроблених 16 прийомами теодолітом 2Т5.
Приклад 5.1. Результати вимірів:
L1= 115° 14' 42,1''; L7= 115° 14' 29,8''; L13= 115° 14' 32,0'';
L2= 115° 14' 35,2''; L8= 115° 14' 29,1''; L14= 115° 14' 41,4'';
L3= 115° 14' 35,4''; L9= 115° 14' 35,3''; L15= 115° 14' 21,5'';
L4= 115° 14' 34,4''; L10= 115° 14' 39,0''; L16= 115° 14' 34,6'';
L5= 115° 14' 28,7''; L11= 115° 14' 32,1'';
L6= 115° 14' 37,3''; L12= 115° 14' 27,5'';
Враховуючи рекомендації першої процедури,за значення умовного нуля приймемо величину L0=115° 14' 30,0''. Знайдемо значення величин δli=L0–li і підсумуємо їх. Результати двох процедур наведено в табл. 5.1.
Виконуючи другу процедуруобчислимо за формулою (5.17) просту арифметичну середину, округлимо отриманий результат до 0,1'' і визначимо величину зсуву β за формулою (5.19).
Таблиця 5.1 – Вихідні дані|виміри| і проміжні результати
їх математичної обробки
| № з/п | Результати вимірів li | | δli (с) | δli2 | vi (с) | (vi')2 |
| 115° 14' 42,1'' | 12.1 | 146.4 | -8.6 | 74.0 | |
| 115° 14' 35,2'' | 5.2 | 27.0 | -1.7 | 2.9 | |
| 115° 14' 35,4'' | 5.4 | 29.2 | -1.9 | 3.6 | |
| 115° 14' 34,4'' | 4.4 | 19.4 | -0.9 | 0.8 | |
| 115° 14' 28,7'' | -1.3 | 1.7 | 4.8 | 23.0 | |
| 115° 14' 37,3'' | 7.3 | 53.3 | -3.8 | 14.4 | |
| 115° 14' 29,8'' | -0.2 | 3.7 | 13.7 | ||
| 115° 14' 29,1'' | -0.9 | 0.8 | 4.4 | 19.4 | |
| 115° 14' 35,3'' | 5.3 | 28.1 | -1.8 | 3.2 | |
| 115° 14' 39,0'' | 9.0 | 81.0 | -5.5 | 30.2 | |
| 115° 14' 32,1'' | 2.1 | 4.4 | 1.4 | 2.0 | |
| 115° 14' 27,5'' | -2.5 | 6.2 | 6.0 | 36.0 | |
| 115° 14' 32,0'' | 2.0 | 4.0 | 1.5 | 2.2 | |
| 115° 14' 41,4'' | 11.4 | 130.0 | -7.9 | 62.4 | |
| 115° 14' 21,5'' | -8.5 | 72.2 | 12.0 | 144.0 | |
| 115° 14' 34,6'' | 4.6 | 21.2 | -1.1 | 1.2 | |
| L0=115° 14' 30,0'' | [δl]=55,4 | [(δli)2] =624,9 | [vi']=0,6 | [(vi')2]=433,0 | |
| [δl]/n=3,46'' | nβ=0,64 | ||||
| L'=115° 14' 33,5'' | |||||
| β=0,04 |
Відповідно до третьої процедуриобчислимо зсув, який утворюється за рахунок округлення найймовірніших поправок v' і підсумуємо їх
(див. стовпець 5 табл. 5.1).
Виконаємо контрольну, четверту процедуру, і порівняємо [v'] з величиною nβ. Результат порівняння показує, що величина [v'] на 0,04 менше величини nβ. Отже, обчислення виконані правильно.
П’ята процедуразабезпечує обчислення квадратів (δli)2 і (vi')2.
Відповідно до шостої процедуризробимо обчислення значень емпіричної середньої квадратичної похибки m спочатку за формулами (5.12) і (5.23), а потім використовуючи формули (5.12) і (5.24).
Зробимо елементарні перетворення формули (5.12) і підставивши до неї двічі чисельні значення, отримані при обчисленні [v2] за формулами (5.23) і (5.24), матимемо:
- результат обчислення|підрахунку| емпіричної середньої квадратичної| похибки із використанням чисельних розрахунків за формулою (5.23)
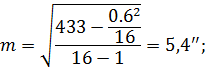
- результат обчислення|підрахунку| емпіричної середньої квадратичної| похибки із використанням чисельних розрахунків за формулою (5.24)
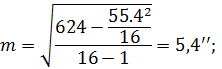
Рівність отриманих результатів показує правильність математичних розрахунків емпіричної середньої квадратичної похибки|підрахунків|.
Оцінювання надійності обчислення наближеного значення емпіричної середньої квадратичної похибки результатів вимірів здійснюється за сьомою процедуроюіз використанням формули (5.25). Підставляючи до формули чисельне значення m = 5,4'' отримаємо
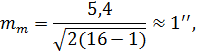
що свідчить|засвідчує| про високу надійність наближеного оцінювання емпіричної середньої квадратичної| похибки результатів вимірів|вимірів|.
Восьмою процедуроюобчислюється середня квадратична| похибка знаходження простої арифметичної середини вимірюваної величини L. Підставляючи до формули (5.26) отримані чисельні значення, маємо
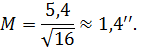
Остаточною, дев’ятою процедурою, здійснюється оцінювання надійності отриманих результатів вимірів. Для цього обчислюється за формулою (5.27) значення середньої квадратичної| похибки результатів вимірів
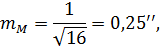
яке порівнюється з|із| сумарною ймовірною| похибкою. У нашому випадку середня квадратична| похибка майже в два з|із| половиною рази менша сумарної найймовірнішої| похибки, що свідчить|засвідчує| про задовільну надійність отриманих результатів.
Таким чином, на підставі раніше розглянутих|розглядувати| понять простої арифметичної середини і її властивостей, а також теореми про знаходження емпіричної середньої квадратичної| похибки сформована строга|сувора| послідовність математичної обробки ряду|лави| рівноточних| результатів вимірів|вимірів|. Математична обробка включає десять|десятеро| процедур, що забезпечують як обчислення|підрахунки| необхідних величин, так і контроль правильності їх виконання. Наводиться конкретний приклад математичної обробки результатів вимірів|виміру| горизонтального кута|рогу|, що показує працездатність сформованої послідовності математичних побудов|шикувань|.
| <== попередня сторінка | | | наступна сторінка ==> |
| Основна теорема теорії похибок | | | Одиниці ваги |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |