• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Одиниці ваги

В основу математичних побудов, що призводять до формального представлення емпіричної середньої квадратичної похибки одиниці ваги вимірів покладемо обґрунтування першої властивості загальної арифметичної середини, а саме формулу (6.20). За аналогією з випадком рівноточних вимірів (див. п.п. 5.3, формула (5.26)) невідомий стандарт вимірів σ_L і стандарт одиниці ваги 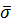замінимо середньоквадратичними похибками, отримаємо

де М – середня квадратична похибка загальної арифметичної середини μ – середня квадратична похибка одиниці ваги.

Для оцінки точності загальної арифметичної середини окрім ваг необхідно за наслідками вимірів знайти середньоквадратичну похибку одиниці ваги μ.

Для розв’язання поставленого завдання|задачі| наведемо доведення наступної|такої| теореми.

Теорема 6.1. Якщо v₁, v₂,…, v_n відхилення від загальної арифметичної середини, незалежних результатів вимірів, вільних від змінних систематичних похибок, то величина

є|з'являється| спроможним і незміщеним наближенням до квадрата стандарту (дисперсії) одиниці ваги.

Якщо змінні систематичні похибки відсутні в результатах вимірів|вимірів|, то відповідно до другої властивості вони відсутні і в загальному|спільній| арифметичному середньому.

Як і у разі|в разі| доведення теореми (див. п.п. 5.2, формула 5.12) про те, що найймовірніші| поправки є дійсне і незміщене наближення до квадрата стандарту і на підставі формул (5.13) і (5.14) отримаємо|одержуватимемо| співвідношення для розрахунку найймовірніших| поправок нерівноточних| вимірів

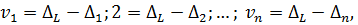|вимірів|

де Δ_L – істинно випадкова похибка арифметичної середини 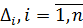– випадкові істинні похибки результатів вимірів|вимірів|.

Перетворимо отриману|одержувати| систему рівнянь наступними|такими| методами. По-перше, поміняємо місцями праві і ліві частини|частки| кожного з рівнянь, по-друге, піднесемо до квадрата праві і ліві частини|частки| рівнянь і, по-третє, перетворимо їх відповідно до формул скороченого множення многочленів. У результаті отримаємо

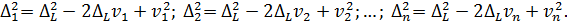
Помножимо кожен з цих виразів на відповідну йому вагу 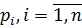і почленно їх підсумуємо. Це призводить до наступного формального виразу 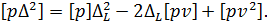Враховуючи четверту властивість загальної арифметичної середини, а саме, що [pv]=0 і, перетворюючи рівняння, отримаємо

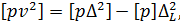
Помножимо ліву і праву частини рівняння на отримаємо

і перейдемо до границі за n→∞

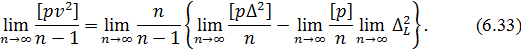
Розглянемо|розглядуватимемо| границі правої частини|частки| виразу|вираження| (6.33).

1. При доведенні теореми в п.п. 5.2 вже показано, що

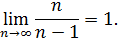
2. Для дослідження границі 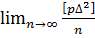помножимо результати вимірів на корені квадратні з їх вагів 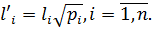Величини l'_i відповідно до (6.7) мають ваги, рівні одиниці, отже, їх можна розглядати як результати рівноточних вимірів, а їх випадкові похибки 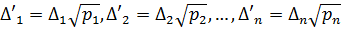мають стандарт, що дорівнює стандарту одиниці ваги 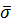. Тому на підставі властивості розсіювання випадкових похибок (2.14) можемо записати

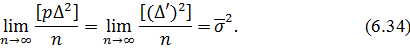
3. Визначимо, чому дорівнює границя . Враховуючи обмежувальні умови на ваги, які розглядалися в п.п.6.3, а саме 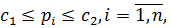має місце нерівність 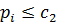. Підсумуємо ці нерівності від p_i до p_n отримаємо [p]≤nc₂. Розділивши ліву і праву частини отриманої нерівності на n і переходячи до границі, знайдемо

4. На підставі третьої властивості загальної|спільної| арифметичної середини можна підсумувати, що

Підставляючи границі (6.34), (6.35) і (6.36) до виразу|вираження| (6.33) і зважаючи на|беручи до уваги| обмеженість величини (6.35), переходимо до межі

що і доводить спроможність оцінки (6.31). Перша частина|частка| теореми доведена.

Для доказу незміщеності| оцінки (6.31) припустимо|передбачатимемо|, що є|наявний| t| рядів|лав| результатів незалежних нерівноточних | вимірів|вимірів|:

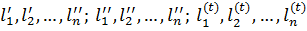
з вагами p₁, p₂,…, p_n. Тоді цей доказ зводиться до доказу незміщеності оцінки

де μ₁, μ₂,…, μ_t – величини, обчислені за формулою (6.31) для кожного з наведених вище рядів вимірів. На підставі формул (6.31) і (6.32) запишемо

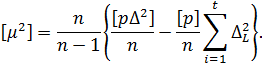
Розділимо цей вираз почлено на t і перейдемо до межі t→∞ матимемо рівняння

Розглянемо|розглядуватимемо| границі в правій частині|частці| отриманого|одержувати| виразу|вираження|. Відповідно до формули (6.34)

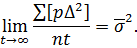
Позначимо Δ_L1, Δ_L2,…, Δ_Lt – випадкові похибки загальних арифметичних середніх, а L', L'',…, L^(t) випадкові похибки рівноточних величин, що мають одну і ту саму вагу [p]. На підставі властивості розсіювання випадкових похибок (2.14) приймаємо

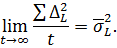
Підставимо ці границі до виразу|вираження| (6.39), отримаємо|одержуватимемо| формулу

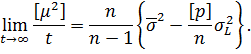
Замінимо σ²_L її значенням з (6.20) і проведемо необхідні перетворення. У результаті отримаємо

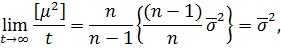
що і доводить незміщеність оцінки (6.31), яку називають емпіричною середньою квадратичною похибкою одиниці ваги. Доведена друга частина теореми.

Надійність величини, обчисленої за формулою (6.31), як і у разі рівноточних|в разі| | вимірів|вимірів|, може бути оцінена за допомогою наближеної формули

На підставі формули (6.37) дійдемо висновку, що якщо відомі істинні випадкові похибки ряду нерівноточних|лави| | вимірів|вимірів| однієї і тієї ж величини, середня квадратична| похибка одиниці ваги може бути обчислена за формулою

а її надійність оцінена за наближеною формулою:

Таким чином, на основі доведення теореми отримана|одержувати| формула для розрахунку однієї з точностних | характеристик нерівноточних| вимірів|вимірів| – емпіричної середньої квадратичної| похибки одиниці ваги.

6.5. Послідовність математичної обробки ряду нерівноточних|лави| |

вимірів|вимірів| однієї і тієї ж величини

За аналогією з організацією послідовності математичної обробки ряду рівноточних|лави|| вимірів|вимірів| (див. п.п. 5.3) задамо послідовність математичних процедур для ряду нерівноточних|лави| | вимірів|вимірів| однієї і тієї ж величини.

Процедура 1. Обчислення вагів результатів вимірів. Залежно від конкретних умов вимірювання використовується один із виразів:

- формула (6.1), коли стандарти результатів вимірів|вимірів| відомі і можуть бути визначені теоретично;

- формула (6.9), коли стандарти невідомі;

- формула (6.10) у разі|в разі| рівності стандартів (див. приклад|зразок| 6.1 в п.п.6.2);

- формула (6.13) у разі|в разі| лінійних вимірів|вимірів| і відсутності систематичних похибок (див. приклад|зразок| 6.2 в п.п. 6.2);

- формула (6.14) у разі|в разі| вимірів|виміру| перевищення, нівелірного|нівелір| ходу, прокладеного у рівнинній місцевості|місцевий| (6.15),| (див. приклад|зразок| 6.3 в п.п. 6.2).

Процедура 2. Обчислення загальної арифметичної середини за формулою (6.17) і найймовірніших поправок за формулою .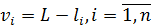

Особливістю процедури є те, що обчислення переважно виконуються з округленнями, замість L приймаємо її наближене значення L' а замість поправок v_i – їх зміщені величини .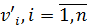

Процедура 3. Контрольна перевірка правильності обчислення найймовірніших поправок, яка здійснюється з використанням формули

Процедура 4. Обчислення зсуненого значення суми [pv²]. Для цього застосовується формула 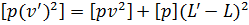яка отримана при доказі п'ятої властивості загальної арифметичної середини. Перетворюючи цей вираз знаходимо

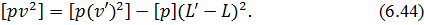
Процедура 5. Контроль правильності обчислення за формулою (6.44), який здійснюється шляхом розрахунку цієї ж величини, але за іншою
формулою

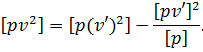
Якщо результати обчислення|підрахунку| однакові, то виконується наступна|така| процедура.

Процедура 6. Обчислення середньоквадратичної похибки одиниці ваги μ шляхом підстановки значення [pv²] до формули (6.31).

Процедура 7. Оцінка надійності отриманого результату з використанням формули (6.40).

Процедура 8. Обчислення середньої квадратичної похибки загальної арифметичної середини М за формулою (6.30).

Процедура 9. Оцінка надійності отриманого результату з використанням формули

Таким чином, розглянуті|розглядувати| особливості нерівноточних | вимірів|вимірів| і на цій підставі наведена послідовність математичних процедур їх обробки.

Переглядів: 1032