Відсутність залежності

Рис. 8.4 – Ілюстрація відсутності залежності між результатами

вимірів|вимірів|

Основною ознакою, підтверджуючою відсутність залежності, є|з'являється| границя

Окремим випадком границі (8.1) є|з'являється| властивість незалежності випадкових похибок, представлена|уявляти| границею (1.12).

8.2. Кількісні характеристики лінійної стохастичної|самодифузія| залежності

Лінійна стохастична залежність не може бути точно виражена функціональною залежністю, наприклад, у вигляді параболи, зображеної на рис.8.1, або іншими чіткими залежностями – логарифмічною, показниковою і так далі. Разом з тим, існують кількісні характеристики, що точно описують взаємозалежність між величинами x і у. Вивченням кількісних характеристик, що описують залежність зв'язків між випадковими величинами займається теорія кореляції.

Кореляція– статистичний взаємозв'язок двох або декількох випадкових величин (або величин, які можна з деякою припустимою мірою точності вважати такими). При цьому, зміни однієї або декількох з цих величин призводять до систематичної зміни іншої або інших величин.

Однією з характеристик оцінки тісноти зв'язку за дослідними (апостеріорними) даними величин x і у є кореляційний момент

де n – об'єм|обсяг| вибірки, тобто кількість пар x, y|;

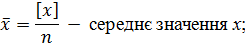
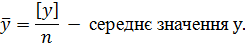
Величина k залежить від розмірності величин x і у|біля| і тому вона не зовсім зручна для оцінювання тісноти зв'язку цих величин.

Найбільш ефективним критерієм оцінювання тісноти зв'язку виміряних|виміряти| геодезичних величин є|з'являється| вибірковий коефіцієнт кореляції, що обчислюється за формулою

; .

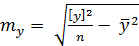Властивості коефіцієнта кореляції:

1. Коефіцієнт кореляції набуває значень в інтервалі від -1 до +1, тобто справедлива нерівність -1 ≤ r ≤ +1.

2. Коли коефіцієнт кореляції дорівнює +1 або -1, між величинами x і у|біля| існує лінійна функціональна залежність вигляду|виду|

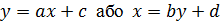
3. Якщо r = 0 то між величинами x і у лінійна залежність відсутня, але можуть існувати складніші залежності.

Коефіцієнт кореляції, обчислений за дослідними даними в загальному випадку є величиною випадковою. Тому при значеннях r < 0,5 виникає наступне питання: чи підтверджує обчислене значення r наявність стохастичного зв'язку величин x і у або воно є наслідком якихось випадкових чинників? Іншими словами, чи є r величиною значущою?

При n > 50 критерієм значущості може бути середня квадратична похибка

При n < 50 критерієм значущості можуть служити критичні значення коефіцієнта кореляції за r = 0 наведені в табл. 8.1. Якщо при об'ємі вибірки n і заданій вірогідності 0,75; 0,90;…;0,995 обчислене значення r більше наведеного в таблиці, то з вірогідністю p можна стверджувати, що r > 0 і стохастична залежність між величинами x і y існує.

Таблиця 8.1 – Вихідні|вихідні| дані для оцінювання залежності випадкових величин

n	Ймовірність\|ймовірність\| наявності залежності між випадковими величинами
0.75	0.90	0.95	0.975	0.99	0.995

	0.7071	0.9511	0.9877	0.9969	0.9995	0.9999
	0.5000	0.8000	0.9000	0.9500	0.9800	0.9900
	0.4040	0.6870	0.8054	0.8783	0.9343	0.9587
	0.3473	0.6084	0.7293	0.8114	0.8822	0.9172
	0.3091	0.5509	0.6694	0.7545	0.8329	0.8745
	0.2811	0.5067	0.6215	0.7067	0.7887	0.8343
	0.2596	0.4716	0.5822	0.6664	0.7498	0.7977
	0.2423	0.4428	0.5493	0.6319	0.7155	0.7646
	0.2281	0.4187	0.5214	0.6021	0.6851	0.7348
	0.2161	0.3981	0.4973	0.5760	0.6581	0.7079
	0.2058	0.3802	0.4762	0.5529	0.6339	0.6835
	0.1968	0.3646	0.4575	0.5324	0.6120	0.6614
	0.1890	0.3507	0.4409	0.5140	0.5923	0.6411
	0.1820	0.3383	0.4259	0.4973	0.5742	0.6226
	0.1757	0.3271	0.4124	0.4822	0.5577	0.6055
	0.1700	0.3170	0.4000	0.4683	0.5426	0.5897
	0.1649	0.3077	0.3887	0.4555	0.5285	0.5751
	0.1602	0.2992	0.3783	0.4438	0.5155	0.5614
	0.1558	0.2914	0.3687	0.4329	0.5034	0.5487
	0.1518	0.2841	0.3598	0.4227	0.4921	0.5368
	0.1481	0.2774	0.3515	0.4132	0.4815	0.5256
	0.1447	0.2711	0.3438	0.4044	0.4716	0.5151
	0.1415	0.2653	0.3365	0.3961	0.4622	0.5052
	0.1281	0.2407	0.3061	0.3610	0.4226	0.4629
	0.1179	0.2220	0.2826	0.3338	0.3916	0.4296
	0.1098	0.2070	0.2638	0.3120	0.3665	0.4026
	0.1032	0.1947	0.2483	0.2940	0.3457	0.3801
	0.0976	0.1843	0.2353	0.2787	0.3281	0.3610

Приклад 8.2. За вибіркою n = 16 обчислений коефіцієнт кореляції r = 0,72. На перетині рядка n = 16 і стовпця p=0,995 знаходимо критичне значення, яке дорівнює 0,6226. Оскільки 0,72 > 0,6226, з вірогідністю p=0,995 можемо стверджувати, що величини x і y мають стохастичну залежність. Критичні значення для коефіцієнта кореляції p=0 коли,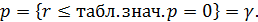

Якщо встановлено, що між величинами x і y – зв'язок істотний, може бути складене так зване рівняння регресії – функція, що описує стохастичний зв'язок

<== попередня сторінка	\|	наступна сторінка ==>
Види залежностей	\|	Залежні випадкові похибки в геодезії

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.