Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Історична довідка

Лагранж Жозеф Луї (25.1.1736, Турин, — 10.4.1813, Париж), французький математик та механік, член Паризької АН (1772). Самостійно вивчав математику. В 19 років став професором в артилерійській школі Турина. В 1759 обраний членом Берлінської Академії наук, а в 1766 – 1787 р. був її президентом. З 1795 р. професор нормальної школи. Лагранжу належать також видатні дослідження з різноманітних питань математичного аналізу (формула залишкового члена ряду Тейлора, формула кінцевих приростів, теорія умовних екстремумів), теорії чисел, алгебри (симетричної функції коренів рівняння), з диференціальних рівнянь (теорія особливих рішень, метод варіації сталих), з інтерполяції, математичної картографії, астрономії та ін.

Характеристика П’єром Симоном Лапласом діяльності Лагранжа …серед тих, хто найефективнішим чином розширив границі наших знань, Ньютон та Лагранж в найвищому ступені володіли щасливим мистецтвом відкриття нових даних, які являють собою сутність знань…

Використаємо доведення теореми Лагранжа. Для цього розглянемо функцію

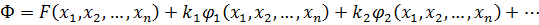
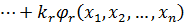, (11.7)

де 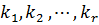– невизначені множники – корелати, які пов’язують між собою умовні змінні .

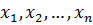Перетворимо функцію Ф в систему рівнянь, прирівнявши послідовно кожну складову формули (11.7) до нуля

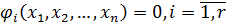а потім прирівняємо до нуля систему з 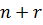рівнянь з 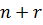невідомими. В скороченому вигляді можна записати:

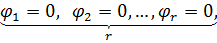
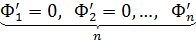Для складання функції Лагранжа помножимо (11.6) на невизначені множники 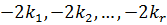. Отримані вирази підсумуємо і додамо до функції .

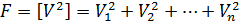В результаті математичних перетворень отримаємо функцію

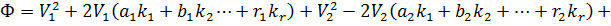
Знайдемо локальні мінімуми в цій функції. Для цього візьмемо часткові похідні за змінними 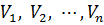і прирівняємо їх до нуля,

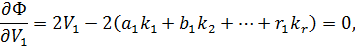
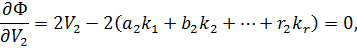
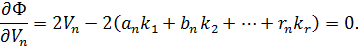
Із отриманої системи рівнянь знаходимо поправки , ,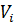

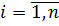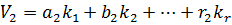Представимо отриману систему рівнянь в матричному вигляді:

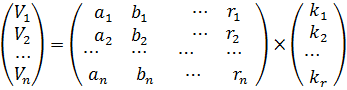
або в скороченому вигляді

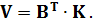(11.8)

Із отриманого співвідношення видно, що для обчислення поправок 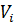до виміряних величин необхідно спочатку визначити матрицю К, яка являє собою вектор невизначених множників Лагранжа, тобто корелат …,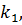

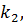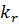
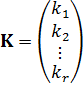Підставимо матрицю 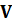із співвідношення (11.8) до формули (11.6) і отримаємо:

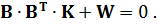(11.9)

Введемо позначення

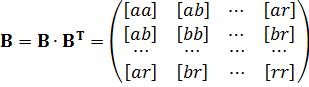. (11.10)

На підставі співвідношення (11.9) і введеного позначення (11.10) можна записати:

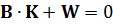. (11.11)

Отриманий вираз являє собою систему нормальних рівнянь, де кількість рівнянь r дорівнює кількості невідомих , .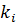

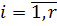Помножимо (11.10) слева на обратную матрицу 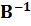, находим столбец коррелат

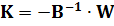. (11.12)

Підставимо значення матриці Ку вираз (11.8), знайдемо стовпчик поправок V.

Контроль правильності перетворень здійснюють наступною процедурою. Помножимо вираз (11.8) зліва на транспоновану матрицю-рядок поправок 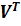. Отримаємо

Виконавши необхідні перетворення, знайдемо 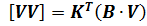, але так як 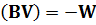, то , що і підтверджує правильність перетворень.

Упорядкуємо розглянуті вище математичні перетворення і задамо строгий порядок процедур зрівнювання виміряних величин, пов’язаних умовами.

Процедура 1.Визначення кількості і виду умовних рівнянь в системі виміряних геодезичних величин.

Процедура 2. Складання умовних рівнянь з нев’язками 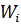, 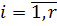та їх обчислення.

Процедура 3. Приведення отриманих рівнянь до лінійного вигляду шляхом розкладення їх у ряд Тейлора (11.4 -11.6).

Процедура 4. Складання матриці коефіцієнтів нормальних рівнянь корелат (11.10).

Процедура 5. Обчислення корелат 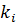, 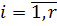з рівняння (11.11).

Процедура 6. Визначення вірогідніших поправок 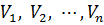підставленням корелат в рівняння (11.8).

Процедура 7. Контроль правильності виконаних математичних перетворень.

Таким чином, розглянута процедура знаходження умовного мінімуму методом найменших квадратів. Приведена послідовність розв’язання нормальних рівнянь корелат.

<== попередня сторінка	\|	наступна сторінка ==>
Знаходження умовного мінімуму методом найменших квадратів.	\|	Оцінка точності функцій зрівняних величин

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.