Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Оцінка точності функцій зрівняних величин

В попередньому підрозділі приведена послідовність визначення поправок, які дозволяють отримати зрівняні значення виміряних величин, що задовольняють умовам (11.3). На практиці у більшості випадків інтерес представляють не самі зрівняні значення виміряних величин (горизонтальних кутів і напрямків, довжин ліній, перевищень і т.д.), а їх функції (координати та висоти точок, площі ділянок та ін.). Тому виникає задача оцінки точності функцій зрівняних значень виміряних величин. Розглянемо сутність вирішення цієї задачі.

Нехай є деяка функція

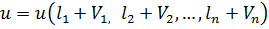. (11.13)

Необхідно знайти її середню квадратичну похибку 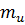. Будемо враховувати, що поправки 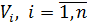отримані з сумісного зрівнювання, а вираз (11.13), є функцією незалежних величин. Тоді оцінка точності функцій зрівняних величин, як і при оцінці точності зрівняних значень невідомих (см. п.10.4), буде мати свої особливості.

Для відокремлення поправок 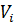від безпосередньо виміряних величин 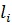розкладемо функцію (11.13) в ряд Тейлора, обмежуючись при цьому першими членами ступеневого ряду, що мають степінь, яка дорівнює одиниці. Тоді аналогічно до рівняння (11.4) справедливо записати

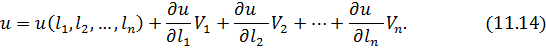
Введемо позначення для часткових похідних

і представимо з урахуванням введених позначень вираз (11.14) в матричному вигляді

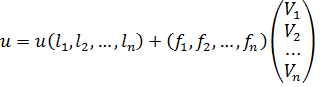. (11.16)

Враховуючи матричну форму представлення умовних рівнянь (11.6) і процедуру їх перетворення для виділення вектора-стовпця 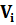(11.8), а також введених позначень для знаходження корелат (11.10) і остаточної формули для їх обчислення (11.12), можна шукану матрицю 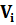представити через матрицю нев’язок умовних рівнянь

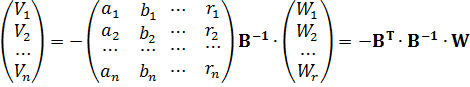.(11.17)

Підставимо отриманий вектор-стовпець в формулу (11.16). Отримаємо

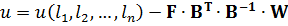де .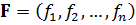

Вираз (11.17) представляє u як функцію незалежних рівноточних вимірів, середні квадратичні похибки яких дорівнюють 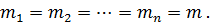Для знаходження середньої квадратичної похибки цієї функції використаємо доказ основної теореми теорії похибок (см.п.10.4) отримаємо:

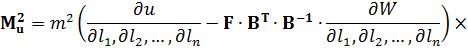
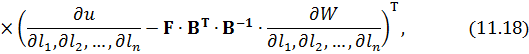
де 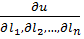і 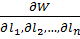– Якобіани. Тоді приймаючи до уваги рівність (11.15), можна записати:

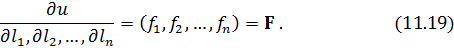
На підставі того, що в результатах рівноточних вимірів існують нев’язки і формально їх записують у вигляді системи рівнянь (11.6), а також позначення (11.5) отримаємо Якобіани нев’язок:

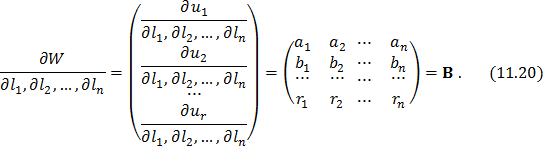
Підставляючи вирази (11.19) і (11.20) в формулу (11.18) отримаємо:

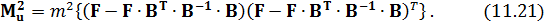
В отриманому виразі формальні представлення, охоплені фігурними дужками мають ліву і праву частини. Вони взяті в круглі дужки. Ліву частину можна представити у вигляді 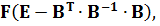де Е – одинична матриця розміром 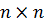, а праву частину, враховуючи симетричність матриці 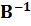іЕперетворити у вираз

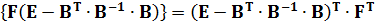Що підтверджує симетричність матриці. Це дає можливість представити вираз (11.21) у вигляді

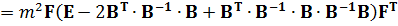Перетворимо отриманий вираз з урахуванням того, що 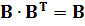, а 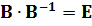, отримаємо:

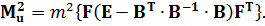(11.22)

Цей вираз представляє собою формулу для обчислення середньої квадратичної похибки функції зрівняних значень безпосередньо виміряних величин.

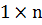Проаналізуємо складові виразу (11.22). Матриця-рядок має розмірність . Матриця, яка представляє різність в круглих дужках має розмірність n 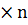, а матриця-стовпець розмірність n .

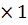Для того щоб переконатися, що в результаті зроблених перетворень не порушена умова рівності кількості лінійних рівнянь і кількості невідомих в них, виконаємо добуток 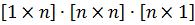, отримаємо матрицю розмірністю 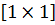, що є свідченням виконання заданих умов.

Нагадаємо, що якщо виконують тільки необхідні вимірювання, то задача зрівнювання не виникає. Тоді в формулі (11.22) вираз в круглих дужках буде дорівнювати одиничній матриціЕ і формула матиме вигляд:

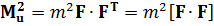Що відповідає середній квадратичній похибці функції безпосередньо і рівноточно виміряних невідомих величин в теорії похибок.

Таким чином, різниця 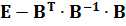(см. формулу (11.22)) представляє кількісну міру зменшення середньої квадратичної похибки зрівняного значення функцій за відношенням до середньої квадратичної похибки, обчисленої за результатами необхідних вимірів.

Формула (11.22) дозволяє оцінити точність однієї єдиної функції зрівняних величин.

Для одночасної оцінки точності z функцій виконаємо аналогічні процедури. Запишемо систему рівнянь

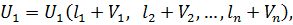
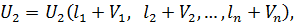
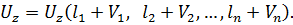(11.23)

Розкладемо кожну функцію (3.23) в ряд Тейлора і позначивши ,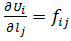

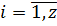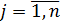, , будемо мати

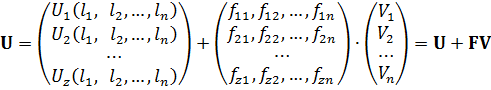. (11.24)

Замінимо в отриманій формулі матрицю-стовпець поправок 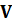добутком матриць ,яке отримано в (11.17) і виконаємо за аналогією всі інші перетворення, отримаємо:

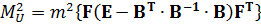. (11.25)

Виразу в фігурних дужках (11.25) відповідає квадратна симетрична матриця розмірністю 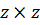. Цей факт дає можливість ввести позначення:

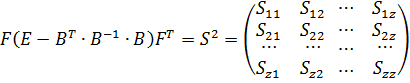, (11.26)

де 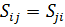умови симетричності матриці (11.26).

З урахуванням прийнятого позначення формула (11.25) прийме остаточний вигляд

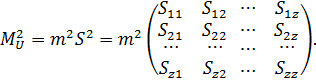(11.27)

Як і в параметричному способі зрівнювання (див.п.2.4) тут елементи матриці S є ваговими коефіцієнтами 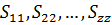, які завжди є додатніми. Вони використовуються для оцінки точності сукупності функцій (11.23). Середні квадратичні похибки цих функцій будуть відповідно дорівнювати :

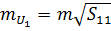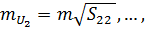
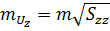, . (11.28)

Елементи 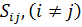матриці (11.27), розташовані з обох боків головної діагоналі, можуть бути як додатніми, так і від’ємними. Вони є кореляційними моментами, які зумовлені залежністю невідомих функцій (11.23).

<== попередня сторінка	\|	наступна сторінка ==>
Історична довідка	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.