• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Властивості

1. Діагоналі прямокутник рівні.

2. Діагоналі ромба взаємно перпендикулярні та ділять кути ромба навпіл.

Ознаки

1. Якщо у паралелограма діагоналі рівні, то такий паралелограм – прямокутник.

2. Якщо у паралелограма діагоналі перпендикулярні, то такий паралелограм – ромб.

3. Якщо у паралелограма діагоналі ділять його кути навпіл, то такий паралелограм – ромб.

Трапеція
Рисунок	Позначення	Формули
	a, b – основи h – висота t – середня лінія S – площа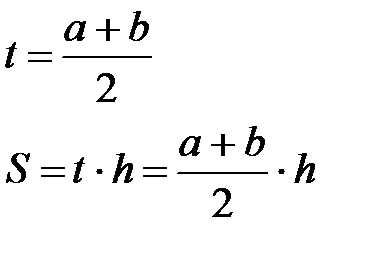
Основні властивості Середня лінія трапеції паралельна основам та дорівнює їх півсумі.
Круг і коло
Рисунок	Позначення	Формули
	R – радіус кола с – довжина кола S – площа круга l – довжина дуги кола Sc – площа сектора a - радіанна міра центрального кута, який відповідає дузі п – градусна міра центрального кута, який відповідає дузі	Центральний кут вимірюється дугою, на яку він спирається. . Вписаний кут вимірюється половиною дуги, на яку він спирається. 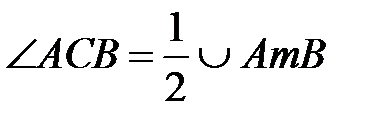. Кут між дотичною і хордою, що проведені через деяку точку кола, вимірюється половиною дуги, що знаходиться між ними. c = 2pR S =pR2
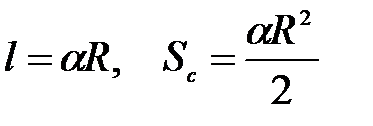
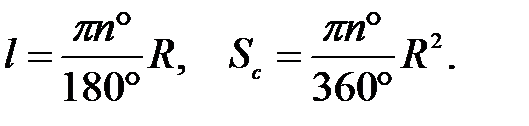
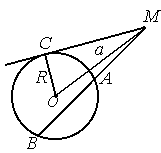
A B C D M Метричні співвідношення у колі Якщо хорди AB і CD перетинаються в точці M у внутрішній частині кола, то Якщо із точки М, що лежить поза колом, провести до кола січну MAB і дотичну MC, то .

Вектор

Вектор - це величина, яка характеризується числовим значенням і напрямком. Під направленим відрізком 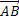розуміють впорядковану пару точок, перша з яких - точка A - називається його початком, а друга - B - його кінцем.

Вектори позначають двома способами:

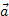· малими буквами латинського алфавіту (наприклад, );

· двома великими буквами латинського алфавіту (наприклад, 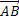), де перша буква - початок вектора, а друга - кінець.

Графічно вектори зображають у вигляді направлених відрізків певної довжини .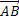

Рис.1. Вектор AB

з початком в A і кінцем в B.

Примітка. Поняття вектора з'явилося в роботах німецького математика XIX ст. Г. Грассмана та ірландського математика У. Гамільтона.

Чисельне значення вектора називається модулем чи довжиною і позначається | 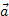|. Довжина вектора - це довжина відрізка, що зображає цей вектор.

Вектори 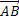і називають протилежно напрямленими, якщо протилежно напрямлені півпрямі і .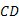

Вектори 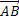і називають співнапрямленими, якщо співнапрямлені півпрямі і .

Рис.2. Протилежно напрямлені вектори.Рис.3. Співнапрямлені вектори.

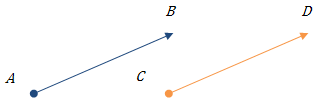
Вектор, початок і кінець якого збігаються, називається нульовим і позначається 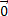. Нульовий вектор має довжину 0. Напрям нульового вектора не визначений. Нульовий вектор прийнято рахувати співнапрямленим з будь-яким вектором. Вважається, що нульовий вектор одночасно паралельний і перпендикулярний будь-якому вектору.

Колінеарними називаються вектори, які зображаються відрізками, що лежать на одній прямій чи на паралельних прямих.

Два вектора називаються рівними, якщо вони однієї довжини і їх напрямки збігаються.

Одиничний вектор (орт) - вектор, довжина якого рівна одиниці.

Числа , називаються координатами вектора 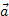з початком 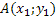і кінцем .

Примітка. Всі координати нульового вектора дорівнюють нулю.

Примітка. Вектори рівні, коли їх відповідні координати рівні.

Вектор з координатами і 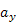позначається .

Вектор з координатами і 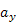позначається .

Використовуючи означення координат вектора довжину можна записати формулою .

Переглядів: 503