• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Етап 4. Побудова лінійної багатофакторної регресії.

Метод найменших квадратів (МНК) дозволяє отримати такі оцінки параметрів a i b,

при яких сума квадратів відхилень фактичних значень результативної ознаки у від

розрахункових (теоретичних) 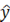є мінімальна:

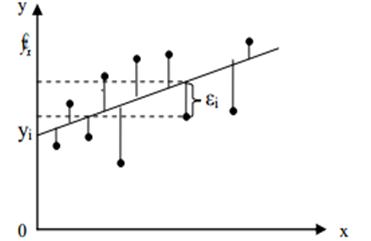
Рисунок 2. Відхилення фактичних значень залежної змінної від теоретичних

Основні припущення МНК:

Припущення 1. Математичне сподівання випадкової величини е дорівнює нулеві. Це

означає, що усереднений чи очікуваний вплив цих помилок на у дорівнює нулеві.

Припущення 2. Відсутність автокореляції між випадковими величинами е. Воно

стверджує, що випадкові величини незалежні одна від одної, тобто будь-яке і-те значення

випадкової величини е не впливає на будь-яке j-те значення цієї величини.

Припущення 3. Гомоскедастичність, або однакова дисперсія випадкової величини е. Це

припущення вимагає, щоб усі випадкові величини, незалежно від номера спостереження,

мали однакову дисперсію. Гетероскедастичність – умовна дисперсія розподілу у

зростає із збільшенням значень х.

Припущення 4. Незалежність між значеннями випадкової величини е і значеннями

змінної х, або нульова коваріація між е та х. Передбачається відсутність зв’язку між цими

двома величинами.

Припущення 5. Регресійну модель визначено (специфіковано) правильно (відсутність

похибки).

Припущення 6. Випадкова величина розподілена нормально з математичним

сподіванням 0 (оскільки сума помилок = 0, тому і середнє = 0) та сталою дисперсією

Етап 5. Перевірити статистичну значущість отриманих результатів:
а) перевірити адекватність моделі загалом: за допомогою F-критерію Фішера перевірити гіпотезу
Н₀ :
проти альтернативної
Н₁: існує хоча б один коефіцієнт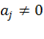
б) перевірити значущість коефіцієнта множинної кореляції, тобто розглянути гіпотезу
Н0 : R = 0
в) перевірити істотність коефіцієнтів регресії:
за допомогою t-критерію Стьюдента перевірити гіпотезу Н0 : =0 для всіх j = 1, 2,..., т проти відповідних альтернативних гіпотез НА : 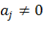для всіх j = 1, 2,..., т;

Етап 6. Оцінити якість побудованої моделі за допомогою різних тестів та критеріїв.Це допомагає остаточно вирішити питання, чи треба змінювати початково обрану модель, та деякі теоретичні припущення. Якщо така зміна необхідна, то треба проводити нові розрахунки і нове тестування.

Переглядів: 842