
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язання
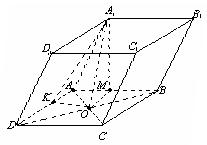
Нехай у паралелепіпеді ABCDA1B1C1D1 : ABCD – квадрат, А1О 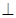 (АВС), точка О – центр квадрата, А1О = Н, АВ = а.
(АВС), точка О – центр квадрата, А1О = Н, АВ = а.
Проведемо ОК 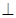 АD, ОМ
АD, ОМ 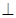 АВ; тоді А1К
АВ; тоді А1К 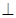 АD, А1М
АD, А1М 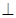 АВ ( за теоремою про три перпендикуляри), тобто А1К і А1М – висоти бічних граней ADD1A1 та ABB1A1 відповідно.
АВ ( за теоремою про три перпендикуляри), тобто А1К і А1М – висоти бічних граней ADD1A1 та ABB1A1 відповідно.
|
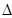 А1ОК =
А1ОК = 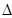 А1ОМ (А1О – спільний катет і ОК = ОМ =
А1ОМ (А1О – спільний катет і ОК = ОМ = 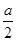 ); звідси: А1К = А1М.
); звідси: А1К = А1М.
Оскільки AD = AB i A1K = A1M, то  , тому
, тому 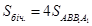 .
.
Із 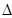 А1ОМ :
А1ОМ : 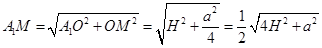 .
.
Тоді 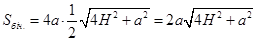 .
.
Відповідь. 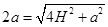 .
.


ЗАДАЧІ
1. Паралелепіпед є чотирикутною призмою. Чи є правильним обернене твердження?
2. Чи існує паралелепіпед, що не є кубом, усі грані якого рівні між собою?
3. Чи є кубом паралелепіпед, у якого рівні між собою всі ребра і плоскі кути при одній з вершин?
4. Чи може перерізом прямокутного паралелепіпеда бути паралелограмом, що не є прямокутником?
5. Куб розрізами на 27 рівних кубиків. У скільки разів загальна площа поверхні отриманих кубиків більша за площу поверхні даного куба?
6. Як зміниться площа поверхні паралелепіпеда, якщо його виміри:
а) збільшити втричі;
б) зменшити вчетверо.
7. Три грані паралелепіпеда – прямокутники. Чи випливає з цього, що даний паралелепіпед прямокутний? Пояснити чому?
8. У паралелепіпеда три грані мають площі 1 м2, 2 м2 і 3 м2. Чому дорівнює повна поверхня паралелепіпеда?
9. Знайдіть виміри прямокутного паралелепіпеда, якщо площі трьох його граней 42 см2, 72 см2 і 84 см2.
10. Дано паралелепіпед, кожна грань якого – ромб із стороною а і кутом α. Знайдіть площу його поверхні.
11. Доведіть, що відрізок, який сполучає центри основ паралелепіпеда, паралельний бічним ребрам.
12. У прямому паралелепіпеді сторони основи 6 м і 8 м утворюють кут 300; бічне ребро дорівнює 5 м. Знайдіть повну поверхню цього паралелепіпеда
13. У прямому паралелепіпеді сторони основи 3 см і 8 см, кут між ними 600. Бічна поверхня дорівнює 220 см2. Знайдіть повну поверхню.
14. У прямому паралелепіпеді сторони основи 3 см і 5 см, а одна з діагоналей основи 4 см. Знайдіть більшу діагональ паралелепіпеда, знаючи, що менша діагональ утворює з площиною основи кут 600.
15. Знайдіть діагоналі прямого паралелепіпеда, кожне ребро якого дорів-нює а, а один з кутів основи дорівнює 600.
16. Бічне ребро прямого паралелепіпеда дорівнює 5 м, сторони основи дорівнюють 6 м і 8 м, а одна з діагоналей основи дорівнює 12 м. Знайдіть діагоналі ромба.
17. У прямому паралелепіпеді бічне ребро дорівнює 1 м, сторони основи дорівнюють 23 дм і 11 дм, а діагоналі основи відносяться як 2 : 3. Знайдіть площі діагональних перерізів.
18. Знайдіть діагоналі прямокутного паралелепіпеда за трьома його вимірами: а) 1, 2, 2; б) 2, 3, 6; в) 6, 6, 7.
19. У прямокутному паралелепіпеді сторони основи 7 дм і 24 дм, а висота паралелепіпеда 8 дм. Знайдіть площу діагонального перерізу.
20. Знайдіть третій вимір прямокутного паралелепіпеда, якщо два його виміри дорівнюють 6 см і 7 см, а діагональ паралелепіпеда дорівнює 11см.
21. Виміри прямокутного паралелепіпеда дорівнюють 3 см, 2 см і 6 см. Знайдіть:
а) довжину діагоналі паралелепіпеда;
б) довжину діагоналі найменшої грані;
в) площу найбільшої грані;
г) площу найменшої грані;
д) площу поверхні паралелепіпеда.
22. У прямокутному паралелепіпеді сторони основи дорівнюють a i b. Діагональ паралелепіпеда утворює з площиною основи кут α. Знайдіть бічне ребро.
23. У прямокутному паралелепіпеді діагональ d утворює з площиною основи кутα, а з бічною гранею -- кут β. Знайдіть виміри паралелепіпеда.
24. Знайдіть поверхню прямокутного паралелепіпеда за трьома його вимірами: 10 см, 22 см, 16 см.
25. Знайдіть бічну поверхню прямокутного паралелепіпеда, якщо його висота h, площа основи Q, площа діагонального перерізу М.
 КОНТРОЛЬНІ ЗАПИТАННЯ
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Дайте означення паралелепіпеда.
2. Назвіть основні властивості граней і ребер паралелепіпеда.
3. Сформулюйте відомі вам властивості діагоналей паралелепіпеда.
4. Який паралелепіпед називається прямим?
5. Який паралелепіпед називається похилим?
6. Який паралелепіпед називається прямокутним? Що таке лінійні розміри прямокутного паралелепіпеда?
7. Яка фігура лежить в основі паралелепіпедів: прямого, похилого та прямокутного?
8. Якою фігурою є грані паралелепіпедів: прямого, похилого та прямокутного?
9. Дайте означення куба.
10. Назвіть основні властивості куба.
11. За якою формулою можна знайти площу основи довільного паралелепіпеда, прямокутного паралелепіпеда, куба?
12. Чому дорівнює площа бічної поверхні паралелепіпеда?
13. Чому дорівнює площа повної поверхні паралелепіпеда?
14. Чому дорівнює площа бічної та повної поверхні куба?
Тема: Розв’язування задач на властивості піраміди та знаходження площі її поверхні.
Мета заняття: формування вмінь розпізнавати і знаходити невідомі елементи піраміди і зрізаної піраміди та знаходження площ їх поверхонь.

| <== попередня сторінка | | | наступна сторінка ==> |
| РОЗГЛЯНЕМО ПРИКЛАДИ | | | ПІРАМІДА |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |