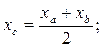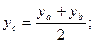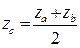МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Багатогранний кут

|
|
|
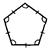

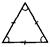
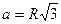

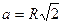
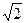
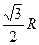

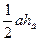 ; S =
; S = 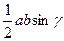 ; S =
; S = 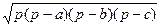 , р=
, р=  - формула Герона; S= pr; S=
- формула Герона; S= pr; S= 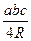 .
.
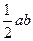
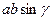 ; S =
; S = 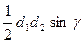 .
.
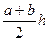
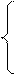 AC2=AD×AB;
AC2=AD×AB;
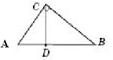
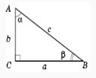 CD2= AD×DB;
CD2= AD×DB;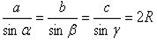
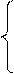
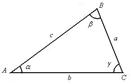
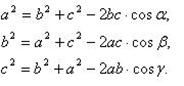
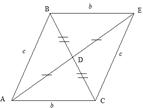 АЕ2 + ВС2 = 2(АВ2 + ВЕ2)
АЕ2 + ВС2 = 2(АВ2 + ВЕ2)
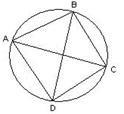 AC×BD=AB×CD+BC×AD
AC×BD=AB×CD+BC×AD
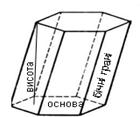
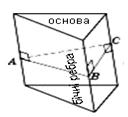
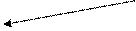 Трикутна призма Шестикутна призма
перпендикулярний переріз
Трикутна призма Шестикутна призма
перпендикулярний переріз


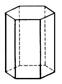
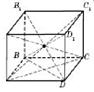 Якщо основою призми є паралелограм, то вона називається паралелепіпедом.
Якщо основою призми є паралелограм, то вона називається паралелепіпедом.
 Прямий паралелепіпед:
Бічні ребра перпендикулярні
до основ.
Бічні грані - прямокутники,
а основи – паралелограми.
Прямий паралелепіпед:
Бічні ребра перпендикулярні
до основ.
Бічні грані - прямокутники,
а основи – паралелограми.
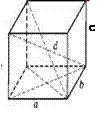 Прямокутний паралелепіпед:
Бічні грані - прямокутники.
Всі діагоналі рівні.
d2 = a2 + b2 + c2
Sповн. = 2(ab+dc+ac)
V = a b c
Прямокутний паралелепіпед:
Бічні грані - прямокутники.
Всі діагоналі рівні.
d2 = a2 + b2 + c2
Sповн. = 2(ab+dc+ac)
V = a b c
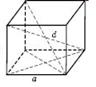 Куб:
Всі грані - квадрати.
Всі ребра рівні.
d =
Куб:
Всі грані - квадрати.
Всі ребра рівні.
d = 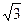 a
Sповн. = 6a2
V = a3
a
Sповн. = 6a2
V = a3
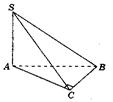
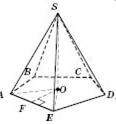 Висотою пірамідиназивається перпендикуляр, опущений з вершини піраміди на площину
Висотою пірамідиназивається перпендикуляр, опущений з вершини піраміди на площину 

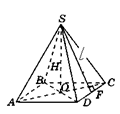 Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника.
Віссюправильної піраміди називається пряма (SO), яка містить її висоту.
Бічні ребра рівні, бічні грані - рівні рівнобедрені трикутники.
Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою (SF)й позначаєтьсяl.
Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника.
Віссюправильної піраміди називається пряма (SO), яка містить її висоту.
Бічні ребра рівні, бічні грані - рівні рівнобедрені трикутники.
Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою (SF)й позначаєтьсяl.
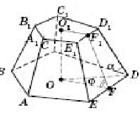 трапеції.
трапеції.
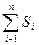 , Si – площа однієї бічної грані,
n – кількість сторін основи
Правильна піраміда
Sбіч.=
, Si – площа однієї бічної грані,
n – кількість сторін основи
Правильна піраміда
Sбіч.= 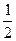 Р× l , Р- периметр основи, l - апофема
Р× l , Р- периметр основи, l - апофема
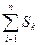 , Sk – площа k-тої бічної грані (трапеції),
n – кількість сторін основи
Правильна зрізана піраміда
Sбіч.=
, Sk – площа k-тої бічної грані (трапеції),
n – кількість сторін основи
Правильна зрізана піраміда
Sбіч.= 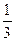 Н ×Sосн.
Н ×Sосн.
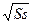 + s)
+ s)
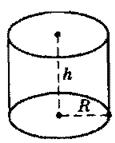
 Утворений обертанням прямокутника навколо однієї з своїх сторін
Утворений обертанням прямокутника навколо однієї з своїх сторін
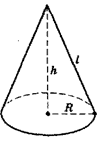 Круговим конусом називається тіло, яке складається з круга - основи конуса, точки, яка не лежить у площині цього круга - вершини конуса і всіх відрізків, що сполучають вершини конуса з точками основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються твірними конуса (l).
Круговим конусом називається тіло, яке складається з круга - основи конуса, точки, яка не лежить у площині цього круга - вершини конуса і всіх відрізків, що сполучають вершини конуса з точками основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються твірними конуса (l).
 Утворений обертанням прямокутного трикутника навколо
одного з катетів
Утворений обертанням прямокутного трикутника навколо
одного з катетів
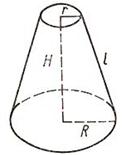 Утворений обертанням прямокутної трапеції навколо перпендикулярної до основ бічної сторони
Утворений обертанням прямокутної трапеції навколо перпендикулярної до основ бічної сторони

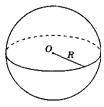 Сфера є поверхнеюкулі.
Утворена обертанням півкола наколо діаметра
Сфера є поверхнеюкулі.
Утворена обертанням півкола наколо діаметра
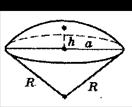
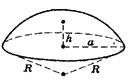 Кульовий сектр Кульовий сегмент
a2=h(2R-h)
Кульовий сектр Кульовий сегмент
a2=h(2R-h)

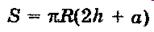
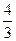 pR3
pR3
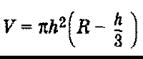
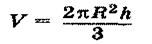
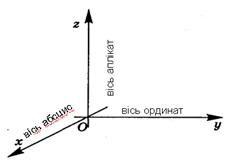 Нехай х, у, z — три попарно перпендикулярні координатні прямі, які перетинаються в точці О.
Ці координатні прямі називаютьсякоординатними осями: вісьх, вісь у, вісь z або вісь абсцис, вісь ординат, вісь аплікат відповідно, точку О називаютьпочатком координат.
Кожна вісь точкою О розбивається на дві півосі — додатну, позначену стрілкою, і від'ємну.
Площини, які проходять через х і у, х і z, у і z, називають координатними площинами і позначають відповідно: ху, хz, уz.
Координатні площини розбивають весь простір на вісім частин, які називають октантами.
Відстань між двома точкамиА (XA; YA; ZA) i B (XB; YB; ZB) обчислюється за формулою:
Нехай х, у, z — три попарно перпендикулярні координатні прямі, які перетинаються в точці О.
Ці координатні прямі називаютьсякоординатними осями: вісьх, вісь у, вісь z або вісь абсцис, вісь ординат, вісь аплікат відповідно, точку О називаютьпочатком координат.
Кожна вісь точкою О розбивається на дві півосі — додатну, позначену стрілкою, і від'ємну.
Площини, які проходять через х і у, х і z, у і z, називають координатними площинами і позначають відповідно: ху, хz, уz.
Координатні площини розбивають весь простір на вісім частин, які називають октантами.
Відстань між двома точкамиА (XA; YA; ZA) i B (XB; YB; ZB) обчислюється за формулою: 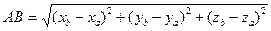 Координати середини відрізкаточки С (Xс; Yс; Zс) - середини відрізка АВ:
Координати середини відрізкаточки С (Xс; Yс; Zс) - середини відрізка АВ: