Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Теорема додавання ймовірностей

У практичній діяльності радіоінженерів зазвичай потрібно визначати ймовірності подій, які не зводяться до схеми випадків, і визначення частот появи яких експериментально ускладнено. Тому на практиці для визначення ймовірностей подій застосовують непрямі методи, що дозволяють по ймовірностях одних подій визначати ймовірності інших подій, з ними пов'язаних. Для цього використовуються основні теореми теорії ймовірностей: теорема додавання й теорема множення ймовірностей.

Розгляд почнемо з теореми додавання ймовірностей двох несумісних подій, що формулюється в такий спосіб.

Імовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій:

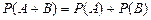. (9)

Доведемо теорему додавання ймовірностей для схеми випадків. Нехай можливі наслідки досліду зводяться до сукупності 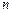випадків. Припустимо, що із цих випадків 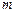сприятливі події 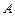, а події 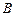, тоді

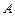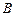Події й несумісні, тому немає таких випадків, які були б сприятливі й 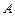і 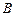разом. Отже, події сприяє випадків і

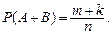
Підставляючи отримані вирази у формулу (9), маємо тотожність. Теорему доведено.

Узагальнимо теорему додавання на випадок трьох несумісних подій. Позначаючи подію літерою й приєднуючи до цієї суми ще одну подію 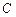, з використанням (9) отримуємо, що

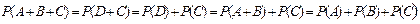Очевидно, що на підставі методу повної індукції теорему додавання можна узагальнити на довільне число 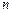несумісних подій

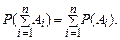(10)

Наслідки, що випливають із теореми додавання ймовірностей.

Наслідок 1. Якщо події утворюють повну групу несумісних подій, то сума їх ймовірностей дорівнює одиниці:

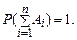
Наслідок 2. Сума ймовірностей протилежних подій дорівнює одиниці:

На практиці досить часто виявляється легше обчислити ймовірність протилежної події 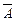, ніж імовірність прямої події 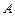. У цих випадках обчислюється Р( 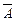), потім шукана ймовірність .

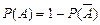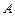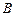У випадку, коли події й сумісні, імовірність суми цих подій виражається формулою

. (11)

Справедливість формули (11) можна підтвердити, розглядаючи рис. 2

Рис. 2.

Аналогічно ймовірність сума трьох сумісних подій обчислюється за формулою

На підставі методу повної індукції можна записати формулу для визначення ймовірності суми будь-якого числа сумісних подій.

Приклад. Радіоканал утворено між приймальним і передавальним центрами, що знаходяться на видаленні друг від друга. При влученні блискавки в антену одного із центрів, зв'язок припиняється (влучення блискавки одночасно у дві антени виключається).

Знайти ймовірність припинення зв'язку, якщо в результаті грози ймовірність влучення блискавки в антену приймального центра становить 0,00004, а в антену передавального центру – 0,00001.

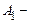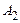Нехай подія порушення зв'язку, подія влучення блискавки в антену приймального центру, влучення блискавки в антену передавального центру. Тоді , причому й несумісні. Тому

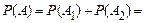0,00004+0,00001=0,00005.

Приклад. Дві наземні радіолокаційні станції незалежно друг від друга провадять виявлення повітряного судна. Імовірність виявлення цілі першою станцією 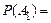0,8, другою – 0,9.

Потрібно знайти ймовірність 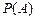виявлення повітряного судна.

За умовою задачі . Події й 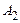сумісні. Тому

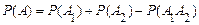Події й 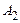, крім того, незалежні, тому 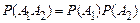й

0,8+0,9 – 0,72=0,98.

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Теорема множення ймовірностей

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.